Automating DBSCAN via Deep Reinforcement Learning阅读笔记

Automating DBSCAN via Deep Reinforcement Learning阅读笔记

文章标题：Automating DBSCAN via Deep Reinforcement Learning

文章链接：https://arxiv.org/abs/2208.04537

代码链接：https://github.com/ringbdstack/drl-dbscan

译者水平有限，如有纰漏，请阅读原文。

摘要

作为一种经典的基于密度的聚类方法，DBSCAN由于简单而且实用，被广泛的运用到许多科学和工程领域中。然而，由于它对聚类距离（$Eps$）和密度阈值（$MinPts$）两个参数的高敏感性，所以聚类的结果严重的依赖于实际的经验。本文中，我们首先提出了一个强化学习指导的自动DBSCAN参数搜索的新框架，即DRL-DBSCAN。此框架将通过感知周围环境来调整参数搜索方向的过程视为一个马尔可夫决策过程，其目的是在没有人工帮助的情况下找到最优的聚类参数。DRL-DBSCAN通过与聚类结果交互，并且使用一个弱监督奖励训练策略网络来学习对于不同特征分布的最优聚类参数的搜索策略。此外，我们也提出了一个由数据规模驱动的递归搜索机制来处理较大的参数空间。我们在基于四个工作模式的五个人工和真实世界数据集上进行了大量的实验。离线和在线任务的结果表明，DRL-DBSCAN不仅分别提升了DBSCAN25%与26%的聚类准确度，而且可以在高计算效率的前提下，稳定的找到合适的参数。此代码已经在GitHub上开源。

关键词 基于密度的聚类，超参数搜索，深度强化学习，递归机制

1 引言

基于密度的噪点空间聚类方法（DBSCAN）是一个典型的根据样本分布的紧密度来决定聚类结构的密度聚类方法。它能够根据数据的特征自动的决定最终聚类的数目，并且对于异常数据不敏感，以及能够发现任何形状的类簇。在应用方面，得益于其对于未知分布数据集的强大适应能力，DBSCAN对于许多聚类问题是首选解，并且在如金融分析[27,53]，商业研究[18,52]，城市规划[37,43]，抗震研究[19,31,50]，推荐系统[25,34]，基因工程[20,41]等领域中由很好的表现。

然而，DBSCAN的两个全局参数，聚类距离Eps和一个类中最少需要的数据点数MinPts，需要人工给定，这给聚类过程带来了三个挑战。第一，参数选择的挑战。Eps和MinPts对于聚类结果有相当大的影响，而且它们需要被提前确定。基于k-距离的方法可以通过曲线上最大变化的位置来估计Eps的可能值，但这仍然需要提前人工的去设置参数MinPts。即使有一些通过避免同时调整Eps和MinPts的DBSCAN的提升方法，但它们也需要提前决定截断距离参数[13]，网格参数[12]，高斯分布参数[47]或者固定的MinPts参数[2,26]。因此，第一个挑战就是如何在没有先验知识来调整参数的前提下实现DBSCAN聚类。第二，适应性策略挑战。由于聚类任务中不同数据分布和聚类特性，传统的基于固定模式[39,40]DBSCAN参数搜索方法在面对非传统数据问题时遇到了瓶颈。并且，使用基于数据标签信息的将外部聚类评价作为目标函数的超参数优化理论[5,30,36]，在没有数据标签信息时效果不佳。只将内部聚类评价作为目标函数的方法[35,37]，尽管不需要标签信息，但却被准确度限制。并且，对于需要持续聚类但数据分布不断变化的流式数据，现有的DBSCAN参数搜索方法没有做到使用过去的经验去自适应的形成对于新数据的参数搜索策略。因此，如何有效和适应性的调整数据的参数搜索策略以及能对应缺失标签信息的情况是第二个挑战。第三，计算复杂度挑战。参数搜索会受到难以估计的大的参数空间的限制。搜索过多无效的参数会增加搜索成本[29]，同时太大的搜索空间也会给聚类准确度带来干扰[14]。所以，如何快速的搜索到最优参数的同时使聚类的准确度得到保证是第三个需要解决的挑战。

近年来，深度强化学习(DRL)[22,38]由于其从环境中能接受反馈的能力[44]被广泛的运用于缺失训练数据的任务中。在本文中，为了解决不能找到最优的DBSCAN参数的问题以及以上的挑战，我们提出了DRL-DBSCAN，一种全新的，自适应的，递归的深度强化学习DBSCAN参数搜索框架，以在多种场景和任务中能稳定地得到最优参数。我们首先将每一步聚类后地聚类的改变情况作为观测状态，参数调整方向视为动作，并且将参数搜索过程视为一个深度强化学习智能体自动感知环境并做出决策的马尔可夫决策过程（图1）。然后，通过弱监督，我们建立了一个基于少量外部聚类指标的奖励，并且基于注意力机制融合了多重聚类的全局状态和局部状态让智能体能够自动学习实现对不同数据场景的自适应参数搜索过程。此外，为了提高学习策略网络的学习效率，我们通过一种基于不同搜索精度的智能体递归机制来优化了基本的框架，以实现在稳定和可控的得到参数的情况下实现较高的聚类准确度。最终，考虑到无标签、少标签、初始数据，增量数据的DBSCAN聚类场景的存在，我们设计了四个工作模式：再训练模式，持续训练模式，预训练测试模式以及考虑到兼容性的维护测试模式。我们在Pathbased，Compound，Aggregation，D31和Sensor数据集上做了大量的离线的任务，以广泛的评价DRL-DBSCAN在四个模式上的参搜搜索表现。结果表明使用DRL-DBSCAN可以不用手动定义参数，即自动并且高效的发现合适的DBSCAN聚类的参数，并且在多种下游任务中具有稳定性。

下面总结了本文的贡献：（1）提出了第一个强化学习指导的DBSCAN的参数搜索框架以自动的选择参数搜索方向；（2）建立了一个弱监督的奖励机制和一个局部聚类状态的注意力机制，可以帮助智能体在缺失标签的情况下根据历史经验来适应性的形成最优参数搜搜策略，实现对数据分布的波动的适应。（3）设计了一个递归的深度强化学习参数搜索策略，提供了对于大范围参数空间搜索问题的一个高效而稳定的解法。（4）通过做了大量离线和在线实验，演示了DRL-DBSCAN的四种模式在提升DBSCAN精度，稳定性和效率方面的优势。

2 问题定义

这一部分，我们给出DBSCAN聚类，DBSCAN聚类的参数搜索，数据流聚类中的参数搜索的定义。

**定义1（DBSCAN聚类）**DBSCAN聚类指对于数据块$V$中的数据对象$\{v_1,...,v_j,v_{j+1},..\}$，依据参数$P=\{Eps,MinPts\}$来划分出类别$C=\{c_1,...,c_n,c_{n+1}...\}$的过程。其中，$Eps$指的是两个相邻点能被划分为一个类的最大距离，$MinPts$指的是一个数据对象要作为一个核心点，其周围（以Eps为半径的圆内）的邻接对象的最小数量。类的形成过程可以被理解为核心点和其周围点（以Eps为半径的圆内）的连接的过程。（图1）

**定义2（离线DBSCAN聚类的参数搜索）**给定数据块$V=\{v_1,...,v_j,v_{j+1},...\}$,DBSCAN的参数搜索记为找到参数空间中最优的参数组合$P=\{Eps,MinPts\}$的过程。其中，数据块$V$的特征集合$X$为$x_1,...,x_j,x_{j+1},...$

**定义3（在线DBSCAN聚类的参数搜索）**给定连续以及暂时的数据块$\{V_1,..V_t,V_{t+1},...\}$作为线上数据流，将在每个时间$t\in T$,从数据块$V_t=\{v_{t,1},...v_{t,j},...,v_{t,j+1},...\}$中找到参数组合$P_t=\{Ep{s}_t,MinPt{s}_t\}$的过程定义为在线聚类的参数搜索。

3 DRL-DBSCAN框架

DRL-DBSCAN有一个核心模型（图2）和四个可以被扩展到下游任务的工作模式（图3）。我们首先描述了参数搜索的基本的马尔科夫决策过程（3.1），以及聚类参数空间和递归机制的定义（3.2）.然后，我们会解释四个DRL-DBSCAN的工作模式（3.3）。

3.1 基于深度强化学习的参数搜索

面对各种聚类任务，固定的DBSCAN参数搜索策略不具有灵活性。我们提出了一种基于深度强化学习的自动的参数搜索框架DRL-DBSCAN，其中核心模型可以被表达为一个包括状态集合，动作空间，奖励函数和策略优化算法马尔可夫决策过程$MDP(\mathcal{S},\mathcal{A},\mathcal{R},\mathcal{P})$[42]。这个过程将DBSCAN的参数搜索过程转化为一个参数空间中的迷宫游戏问题[8,56]，为了训练一个智能体通过与环境交互一步步的从初始点参数搜索到终止点参数，并且终止点（最后一步的参数）作为一局游戏最后的搜索结果（图2）。具体的，智能体将参数搜索空间和DBSCAN聚类算法分别视为环境，搜索的位置与聚类的结果视为状态，参数的调整方向视为动作。另外，我们使用一种弱监督的方法，使用少量标签样本奖励表现良好的智能体，做正向反馈。我们基于Actor-Critic架构优化了智能体的策略。具体的，第e轮的搜索过程具有如下的形式：

• 状态 ：由于状态需要能够尽量准确和完整的代表每一步的搜索环境，我们考虑从两方面来构建状态的表征。

首先，对于整体的搜索和聚类状况，我们使用了一个七元组来描述第$i$步的的全局状态（$i=1,2,...$）:
$$s_{global}^{(e)(i)}=P^{(e)(i)}\cup {\mathcal{D}}_b^{(e)(i)}\cup \{R_{cn}^{(e)(i)}\}$$
其中，$P^{(e)(i)}=\{Ep{s}^{(e)(i)},MinPt{s}^{(e)(i)}\}$是目前的参数组。$D_b^{(e)(i)}$是一系列平方距离的集合，包括$Ep{s}^{(e)(i)}$与其空间的边界$B_{Eps,1}$和$B_{Eps,2}$的距离，$MinPt{s}^{(e)(i)}$与其空间的边界$B_{MinPts,1}$和$B_{MinPts,2}$的距离，聚类后类簇的数量$|{\mathcal{C}}^{(e)(i)}|$与数据框中数据对象的数量$|\mathcal{V}|$的比值$R_{vn}^{(e)(i)}=\frac{|{\mathcal{C}}^{(e)(i)}|}{|\mathcal{V}|}$。其中，在3.2中我们会给出上述参数边界的具体定义。

其次，对于每一个类的情况的描述，对于第$i$步类别$c_n\in \mathcal{C}$的局部状态，我们定义了一个$\{d+2\}$元组：
$$s_{local,n}^{(e)(i)}={\mathcal{X}}_{cent,n}^{(e)(i)}\cup \{D_b^{(e)(i)},|c_n^{(e)(i)}|\}.$$
其中，$X_{cent,n}^{(e)(i)}$是类别$c_n$的中心对象的特征，$d$是特征的维度数目。$D_{cent,n}^{(e)(i)}$是类簇中心对象到整个数据块的中心对象的欧几里得距离。$|c_n^{(e)(i)}|$代表类簇$c_n$中对象的数目。

考虑到在参数搜索过程中，类簇数目在每一步中都会变化，我们使用了注意力机制[48]来将全局状态和多个局部状态编码为一个定长的状态表征：
$$s^{(e)(i)}=\sigma (F_G(s_{global}^{(e)(i)})||{\Sigma }_{c_n\in \mathcal{C}}{\alpha }_{att,n}\cdot F_L(s_{local,n}^{(e)(i)})).$$
其中，$F_G$和$F_L$分别是以全局状态和局部状态为输入的全连接网络。$\sigma$代表ReLU激活函数。$||$代表拼接操作。${\alpha }_{att.n}$是类别$c_n$的注意力权重，计算公式如下：
$${\alpha }_{att,n}=\frac{\sigma (F_S(F_G(s_{global}^{(e)(i)})||F_L(s_{global}^{(e)(i)})))}{{\Sigma }_{c_n\in \mathcal{C}}\sigma (F_S(F_G(s_{global}^{(e)(i)})||F_L(s_{global}^{(e)(i)})))}.$$
我们分别将每个类聚的局部状态和全局状态串联，然后用一个全连接网络$F_S$来打分，并且标准化这个分数作为每个类簇的注意力机制的系数。这个方法建立了当局部类簇明确时，全局搜索情况的注意力机制。同时，它也让不同种的聚类信息在最后的状态表征中有不同的权重，这增加了状态表征中重要类簇的影响力。

• 动作：动作$a^{(e)(i)}$代表第$i$步的参数搜索方向。我们将动作空间定义$\mathcal{A}$为$\{left,rifht,down,up,stop\}$,其中$left$和$right$分别代表减小和增加参数$Eps$。$down$和$up$代表减少和增大参数$MinPts$，而$stop$代表停止搜索。具体的，我们建立了Actor[33]作为策略网络来基于目前的状态$s^{(e)(i)}$来决定动作$a^{(e)(i)}$

$$a^{(e)(i)}=Actor(s^{(e)(i)}).$$

其中$Actor$是一个三层的多层感知机(MLP).

此外，从第$i$步到第$i+1$步的动作-参数变化过程可以如下定义：
$$P^{(e)(i)}\stackrel{a^{(e)(i),\theta }}{⟶}{P}^{(e)(i+1)}.$$
其中，$P^{(e)(i)}$和$P^{(e)(i+1)}$分别时第$i$步和第$i+1$步的参数组$\{Ep{s}^{(e)(i)},MinPt{s}^{(e)(i)}\}$和$\{Ep{s}^{(e)(i+1)},MinPt{s}^{(e)(i+1)}\}$。$\theta$是增加或者减少的动作幅度大小。这一部分将会在3.2详细讨论。注意到当一个动作引起参数超出边界，那么参数应该被设置为边界值，并且相应的边界距离在下一步应该被设置为-1。

• 奖励： 考虑到确切的终止参数点是未知的，但是奖励需要能够激励智能体学习一个较好的参数搜索策略，我们使用了一小部分外部度量的样本作为奖励的基础。我们定义了第$i$步立即的奖励为:

$$\mathcal{R}(s^{(e)(i),a^{(e)(i)}})=NMI(DSBCAN(\mathcal{X},P^{(e)(i+1)},{\mathcal{Y}}^{\prime }))$$

其中，$NMI(,)$代表外部的度量函数，即DBSCAN聚类的标准化互信息(NMI)[16]。$\mathcal{X}$是特征集合。${\mathcal{Y}}^{\prime }$是数据块的一个部分标签集。注意到标签仅仅被用在训练过程中，测试过程的搜索是在没有标签的数据块上进行的。

此外，一轮的最优的参数搜索动作序列是不断向着最优参数的方向调整参数，并且在最优参数点停止搜索。因此，我们考虑同时使用剩余步的立即奖励的最大值和中止点立即奖励作为第$i$步的奖励:
$$r^{(e)(i)}=\beta \cdot max\{\mathcal{R}(s^{(e)(m)},a^{(e)(m)}){|}_{m=i}^I+\delta \cdot \mathcal{R}(s^{(e)(I)},a^{(e)(I)})\},$$
其中，$ R(s^{(e)(I)},a{(e)(I)})$是第$I$步中止参数点的立即奖励。max是用于计算中止前未来的立即奖励的最大值。$\beta$和$\delta$是奖励的影响因子，其中$\beta=1-\delta$。

• 终止: 对于完整一轮搜索过程，我们决定使用如下的终止条件：

$$\begin{gathered} min({\mathcal{D}}_b^{(e)(i)})<0,超出边界停止 \\ i>=I_{max},超出最大步数限制停止 \\ {a}^{(e)(i)}=stop,i>=2,停止动作 \end{gathered}$$

其中，$I_{max}$是一轮搜索中的最大搜索步数。

• 优化： 第e轮的参数搜索过程可以表达为：1)观测目前DBSCAN聚类的状态$s^{(e)(i)}$；2）基于$s^{(e)(i)}$使用$Actor$预测参数调整方向$a^{(e)(i)}$；3）得到新状态$s^{{(e)(i+1)}$4）重复上述过程直到一轮搜索结束，并且在每一步计算出奖励$r}{(e)(i)}$。第$i$步的核心如下:

$${\Gamma }^{(e)(i)}=(s^{(e)(i)},a^{(e)(i)},s^{(e)(i),r^{(e)(i)}}).$$

我们将每一步的$\Gamma$放入缓冲区(?) 来优化策略网络$Actor$，并且定义关键的损失函数为:
$${\mathcal{L}}_c={\Sigma }_{\Gamma \in buffer}^M(r^{(e)(i)}+\gamma \ast Critic(s^{(e)(i+1)},a^{(e)(i+1)})-Critic(s^{(e)(i),a^{(e)(i)}}){)}^2.$$

$${\mathcal{L}}_a=\frac{{\Sigma }_{\Gamma \in buffer}^{M}Critic(s^{(e)(i)},Actor(s^{(e)(i)}))}{M}$$

其中，我们定义了一个三层的多层感知机$Critic$来学习状态的动作价值[33],用来优化$Actor$。并且$\gamma$代表奖励的衰变因子。我们的框架中使用TD3策略优化算法[22]，不过可以使用其他深度强化学习策略优化算法来替代[33,38].

3.2参数空间和递归机制

这一部分，我们定义了前一部分提到的智能体的参数空间和基于不同参数空间的递归搜索机制。首先，为了解决由于不同数据分布引起的参数范围的波动，我们标准化了数据特征，从而将参数Eps得到最大的搜索范围变为$(0,\sqrt{d}]$。和$Eps$不同，参数$MinPts$必须是一个大于0的整数。因此，我们提出根据数据集的维度或者大小来划分出参数$MinPts$的最大搜索范围。随后，考虑到当进行高精度搜索时，庞大的搜索空间会影响效率，我们提出了一种递归机制来实现渐进的搜索。递归过程见图2。我们逐层缩小了搜索的范围并且增加了搜索的精度，并且指派了一个3.1中定义的参数搜索智能体$agen{t}^{(l)}$给第$l$层，使其根据相应的搜索精度和范围要求来搜索到最优的参数组$P_o^{(l)}=\{Ep{s}_o^{(l)},MinPt{s}_0^{(l)}\}$。第$l$层的参数$p\in \{Eps,MinPtS\}$的最小搜索边界$B_{p,1}^{(l)}$和最大搜索边界$B_{p,2}^{(l)}$计算公式如下：
$$\begin{gathered} B_{p,1}^{(l)}:max\{B_{p,1}^{(0)},p_0^{(l-1)}-\frac{{\pi }_p}{2}\cdot {\theta }_p^{(l)}\} \\ {B}_{p,2}^{(l)}:min\{p_0^{(l-1)}+\frac{{\pi }_p}{2}\cdot {\theta }_p^{(l)},B_{p,2}^{(0)}\} \end{gathered}$$
其中，${\pi }_p$时每一层参数搜索空间中参数$p$的可搜索到的参数数目。$B_{p,1}^{(0)}$和$B_{p,2}^{(0)}$是第0层参数p的参数搜索空间边界。$p_o^{(l-1)}\in P_o^{(l-1)}$是上一层搜索到的最优参数，而$p_0^{(0)}$是$B_{p,1}^{(0)}$和$B_{p,2}^{(0)}$中间点。另外，${\theta }_p^{(l)}$是搜索步长，即第$l$层参数$p$的搜索精度，计算公式如下：
$$\begin{gathered} {\theta }_p^{(l)}=\frac{{\theta }_p^{(l-1)}}{{\pi }_p},如果p=Eps \\ {\theta }_p^{(l)}=max\{[\frac{{\theta }_p^{(l-1)}}{{\pi }_p}+\frac{1}{2}],1\},否则 \end{gathered}$$
其中，${\theta }_p^{(l-1)}$是前一层的步长，而${\theta }_p^{(0)}$是参数的最大搜索范围，$[]$是向下取整函数。

• **复杂度讨论：**由上可知，第$L$层递归架构最小的搜索步长为${\theta }_p^{(L)}$。当没有递归加否的计算复杂度为$O(N)$，其中N是参数空间的大小。并且，对于DRL-DBSCAN，在递归机制下第$L$层的只需要$L\ast ({\pi }_p)$，将计算复杂度从$O(N)$减少到$O(logN)$

3.3 提出的DRL-DBSCAN

算法1展示了DRL-DBSCAN核心模型的过程。给定一个数据块$\mathcal{V}$和部分标签${\mathcal{Y}}^{\prime }$，训练过程就是在多轮过程中在每一层进行参数搜索(6-10行)来优化智能体的过程（14行）。在这个过程中，可以不断更新最优的参数组合（基于立即奖励（（7）式）的15行和17行）。为了提高效率，我们建立了一个哈希表来记录搜索到的参数组的聚类结果。另外，我们建立了提前停止机制来在最优参数组不再改变的时候停止来加速训练过程（16行和18行）。在测试过程使用训练好的智能体来在一轮过程中直接搜索，并且不设置提前停止机制。另外，测试过程是不需要标签的，最后一层智能体搜索的终止点参数就是最后的最优参数组合。

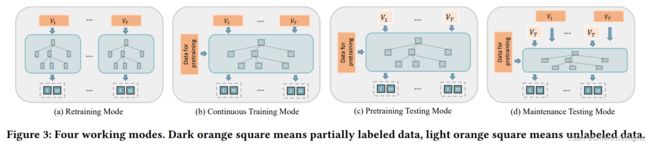
为了更好的适应各种任务情形，我们如图3所示的DRL-DBSCAN的四种工作模式。它们对应于如下的定义：(1)再训练模型($DR{L}_{re}$)：基于训练过程搜索最优参数。当数据集变化时，每一层的智能体被重新初始化。(2)持续训练模型($DR{L}_{con}$):智能体被提前训练。当数据集改变的时候，使用过去已经训练好的智能体基于搜索过程持续搜索。(3)预训练测试模型($DR{L}_{all}$):智能体被提前训练。当数据集改变的时候，直接基于没有标签的测试过程来搜索。(4)维护测试模型($DR{L}_{one}$):智能体被提前训练好。当数据集改变时，直接基于没有标签的测试过程搜索。在预训练之后，定期在有标签的历史数据上进行维护训练。

4 实验

这一部分，我们做了包括以下几部分的实验：（1）比较在离线任务上DRL-DBSCAN和基准线的表现，解释强化学习的搜索过程（4.2部分）；（2）分析DRL-DBSCAN及其变种的表现。比较四种工作模型在在线实验的优点（4.3部分）；（3）超参数及其在模型上的影响的灵敏度分析（4.4部分）。

4.1 实验设置

数据集：为了全面的分析我们的框架，实验的数据集由四个人工聚类基准的数据集和一个公共的现实世界的流式数据集（表1）。基准数据集[21]是2D的集合，包括：Aggregation[23], Compound[55], Pathbased[11], 以及D31[49]。其包含了多种的密度类型比如类聚中的类簇，多密度，多形态，闭环等，并且有各种数据规模。而真实世界的流式数据集Sensor来自伯克利研究所发布的54个传感器数据中的连续数据信息（温度，适度，光强和传感器电压）。我们为实验选了80,864子集并且将其划分为16个数据块$({\mathcal{V}}_1,...,{\mathcal{V}}_{16})$作为在线数据集。

基准线和变体:我们将DRL-DBSCAN与三种类型的基准线相比较：（1）传统的超参数搜索框架：随机搜索算法Rand，基于树结构Parzen估计的贝叶斯最优算法BO-TPE[5]；（2）元启发式优化算法：模拟退火算法Anneal[32]，粒子群优化PSO[46]，遗传算法GA[36]，以及差分进化算法DE[45];(3)现存的DBSCAN参数搜索方法：KDist（V-DBSCAN）[39]和DBE-DBSCAN[30]。以上算法的详细介绍将会在第5部分给出。我们也对4中DRL-DBSCAN的变体做了实验，来分析3.1中建立的状态，奖励和递归机制。与DRL-DBSCAN相比，$DR{L}_{no-att}$不使用基于注意力机制的局部状态。$DR{L}_{only-max}$用最大的特征立即奖励作为最终奖励，$DR{L}_{recu}$不再有停止机制，$DR{L}_{recu}$是没有递归机制的版本。

实现细节： 对于所有的基准线，我们使用了来自基准库Hyperopt[7]和Scikit-opt[1]的开源实现。所有的实验基于Python 3.7，36核3.00GHz因特尔核心$i9$CPU，以及英伟达RTX A6000 GPUS。

实验设置： DRL-DBSCAN的评价是基于3.3中的四个工作模型的。考虑到大多数算法的随机性，所有的实验结果都去了10次基于不同种子的运行结果的平均值（除了KDist因为它是启发式算法并且不带有随机性）。具体的，对于DRL-DBSCAN的预训练和维护训练过程，我们设置了轮数的最大值$E_{max}$为15。在离线任务和在线任务中，递归层数的最大层数$L_{max}$被设置为3和6，以及第0层参数$MinPts$的最大搜索边界$B_{MinPts,2}^{(0)}$和$B_{MinPts,1}^{(0)}$被设置为0.25和0.0025倍的数据块大小。另外我们使用统一的标签训练比例0.2，参数$Eps$空间的大小${\pi }_{Eps}$为5，参数$MinPts$空间的大小${\pi }_{MinPts}$为4，最大搜索步数$I_{max}$为30，奖励因子$\delta $为0.2。而FCN和MLP的维度被均匀的设置为32和256，$Critic$的奖励衰减因子为0.1，从缓冲区的例子数目$M$为16。另外，所有的基准线使用相同的目标函数，参数搜索空间和参数最小步长。

评估标准： 我们使用准确度和效率来评估实验。具体的，我们使用标准化互信息[16]和调兰特指数(ARI)[51]来度量聚类准确度。对于效率，我们用做DBSCAN聚类的次数作为度量。

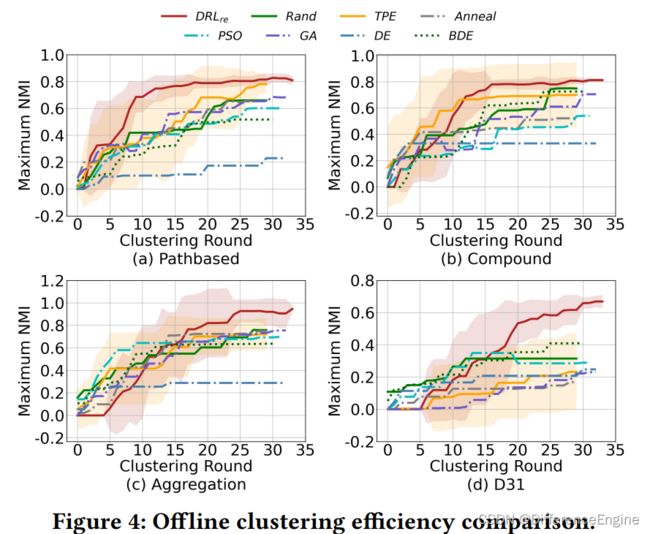
4.2 离线评估

离线评估是基于四种人工基准数据集。由于在离线情形中没有用于预训练的数据，我们将使用了与训练模型的$DR{L}_{re}$的DRL-DBSCAN与基准前的表现作比较。

准确度和稳定性分析： 表2中，我们总结了$DR{L}_{re}$和基准线30次聚类搜索到的最优DBSCAN参数组合的$NMI$和$ARI$的均值和方差。

可以从10次运行的准确度的平均值看出，在Pathbased，Compound，Aggregation和D31数据集中，相对于基准线$DR{L}_e$可以有效地提升$NMI$和$ARI$表现4%和6%，3%和3%，20%和26%，5%和26%。同时，随着数据集规模的增大，$DR{L}_{re}$相比于其他基准线在准确度上的优势不断增加。进一步，从实验方差可以看出，$DR{L}_{re}$相比于基准线，给$NMI$和$ARI$提高了4%和6%，1%和1%，9%和13%，2%和17%。相比于其他的超参数优化基准线，在相同目标函数下，在准确度和稳定性是这样明显的优势说明了$DR{L}_{re}$可以在多轮的参数搜索后可以稳定的找到优秀的参数组。另外，$DR{L}_{re}$不会被数据集的大小影响。在所有的基准线中，PSO和DE在准确度方面是最弱的，因为它们的参数空间是连续的，需要更多次搜索来得到最优结果。BO-TPE通过一个概率代理模型来学习如何提前搜索参数组合，其探索和利用方面的平衡使得它相比于其他的基准线很有优势。我们提出的DRL-DBSCAN不仅通过一个递归机制减小了每一层的搜索空间，而且通过学习历史经验，使得其能够更好的搜索到DBSCAN参数组。

DRL-DBSCAN变种： 我们比较了$DR{L}_{recu}$和$DR{L}_{no-recu}$，即图5中所示的缺少注意力机制的版本。注意到，对于$DR{L}_{recu}$，我们关闭了早期的停止机制以使得其能够搜索足够长时间来更好的与$DR{L}_{no-recu}$比较。结果显示，在第一个100轮种，递归机制给最大搜索速度带来了6.5的增长比率，这有效地说明了注意力机制在效率方面的贡献。

标签部分比较： 考虑到在DRL-DBSCAN训练中标签部分的影响，我们在Pathbased上做了都统标签部分的实验，结果如图6(b)所示（在 以上的竖行是结果的方差）。可以看到在不同的比例标签任务中，$DR{L}_{re}$的平均$NMI$分数比基准线要高，而方差要更小。另外，随着标签数目的减少，大多数基准线的$NMI$分数都会锐减，但是$DR{L}_{re}$基本保持一致。如此稳定的表现展现了DRL-DBSCAN在标签比例改变下有较好的适应能力。

案例学习： 为了更好的展示基于强化学习的参数搜索过程，我们使用了一个3轮的，3层递归，并使用Pathbased数据集的案例（表3）。表三的列代表智能体$agen{t}^{(l)}$在不同轮种的动作序列，终止类型，以及中止点参数组和$NMI$分数。可以观察到DRL-DBSCAN试图从初始的参数组变化到最优的参数组。对于路径依赖形式的搜索，当对于每个参数组都具有沿着路就寻找搜索方向时，可以使用过去学习到的最优路径。由于我们加入了$stop$动作，DRL-DBCSAN可以学习在最优位置停止，这帮猪DRL-DBSCAN在没有标签的线上情况实现聚类。注意到由于我们将过去参数组的聚类信息放入一个哈希表中，所以对于重复的路径不再需额外的操作。

4.3 在线评估

强化学习的可学习性使得DRL-DBSCAN能够更好的利用过去的在线任务的经验。为此，我们全面评估了DRL-DBSCAN在流式数据集上的四种工作模式。具体来说，传感器的前8个模块被用于$DR{L}_{con},DR{L}_{all},DR{L}_{one}$的预训练，而后8个模块用于和基准线比较结果。由于基准线不能在在线任务上实现增量学习，我们在每一块开始前初始化算法。此外，包括$DR{L}_{all}$和$DR{L}_{one}$对于无标签的测试都是用了不可见的数据，而$DR{L}_{one}$在每个模块结束测试后使用做好标签的历史数据对模型进行维护训练。

准确度和稳定性分析： 在表4和表5中，我们给出了DRL-DBCSAN的基于训练的模型（$DR{L}_{re}$和$DR{L}_{con}$）以及基于测试的模型（$DR{L}_{all}$和$DR{L}_{one}$）与基准线的比较。

由于DRL-DBSCAN的动作空间有$stop$动作，所以能够自动的停止搜索。为了控制基准线实验条件的一致，我们使用了DRL-DBSCAN自动结束所消耗的平均聚类次数来作为基准线对应任务的聚类次数（表4为30，表5为16），结果显示在多个模块上，基于训练的模型和基于测试的模型在$NMI$分数的平均值上分别提升了9%和9%，并且方差减少了4%和2%。首先，表4说明了与离线任务类似，基于再训练的$DR{L}_{re}$在在线任务上仍然保留有很大的优势。第二，将$DR{L}_{con}$这个能够进行增量学习的版本与$DR{L}_{re}$相比较，$DR{L}_{con}$在方差上有显著的减少并且使得性能提高14%。第三，从表5中可以发现，在基于测试的模型中，没有标签的$DR{L}_{all}$和$DR{L}_{one}$（没有奖励函数）可以显著的超过需要标签来建立目标函数的基准线。第四，$DR{L}_{one}$，通常都比$DR{L}_{all}$有更小方差和更好表现。这些结果说明了DRL-DBSCAN在保留历史经验方面得能力以及学习到的DBSCAN参数搜索的准确度和稳定性方面的优势。另外，即使$KDist$可以确定没有标签和迭代数时的参数但是相应的准确度会比较低。

效率分析：$DR{L}_{all}$和$DR{L}_{one}$不需要标签来自动地搜索到最优的DBSCAN参数（中止点）。为了更好的分析两个基于测试的参数搜索模型，我们比较了在线任务中，其他方法要达到与$DR{L}_{all}$的中止点相同的$NMI$分数时所需要的聚类次数（图6（a））。在途中，竖列是结果的方差。我们可以看出，$DR{L}_{all}$达到最优结果所消耗的聚类次数范围在11-14之间，而其他的基准线达到相同的$NMI$则需要更多的聚类次数。另外，许多基准线的聚类次数的消耗量在不同的数据块上有严重的波动，同时在同一个数据块上的方差也很大。上述的观测说明了DRL-DBSCAN在缺少标签的基于测试的模型上的参数搜索效率超过了需要标签的基准线。另外，要达到相同的$NMI$，$DR{L}_{con}$比$DR{L}_{re}$所要消耗的聚类次数少，这说明了DRL-DBSCAN在效率方面学习能力的优势。

DRL-DBSCAN变种: 为了更好的评价3.1中状态和奖励的设计，我们比较了$DR{L}_{all}$的两个变种，$DR{L}_{no-attn}$（即状态中没有设置注意力机制）,$DR{L}_{only-max}$（奖励只是基于未来立即奖励中的最大值）。图6（c）的结果显示结构完全的$DR{L}_{all}$在$NMI$分数上比变种要好，并且给最好的表现带来了0.16的提升，这说明设置局部状态和立即奖励的必要性。

4.4 超参数灵敏度

图7展示了对于四个超参数，$DR{L}_{re}$在Pathbased数据集上做离线评估的结果。图7（a）和图7（b）分别比较了方程(13)中参数空间的大小对结果的影响。可以发现对参数$Eps$来说，空间过大或者过小都会带来性能损失和搜索效率的减小，而参数$MinPts$对于参数空间大小的变化则不那么敏感。图7©分析了不同的递归层数对结果的影响。结果显示一个合适的递归层数可以使得性能稳定。值得注意的是，递归层数并不需要太多的调整，因为我们在3.3中以及设置了提前停止的机制来防止出现太多层的情况。图7(d)则比较了中止点立即奖励和未来立即奖励最大值的权重对结果的影响(方程8)。结果显示，比较均衡的分配两个立即奖励的贡献可以帮助DRL-DBSCAN提高性能。

5 相关工作

自动DBSCAN参数决策：作为经典的密度聚类算法，DBSCAN受限于两个需要先验知识进行决定的高灵敏度参数。针对以上的问题，有许多工作提出了相应的解决方案。OPTIC[3]是DBSCAN的一种基于可达性得到$Eps$来建立聚类的拓展。然而，这种方法需要提前确定一个合适的$MinPts$，并且$Eps$需要徐用户交互。V-DBSCAN[39]和KDDClus[40]使用数据对象到它的第近对象的排序距离，并使用曲线上的显著变化的一些值作为候选参数。类似的方法包括 DSets-DBSCAN[26]、Outlier[2]和RNN-DBSCAN[10]，所有这些都需要一个固定的 值或预先确定的最近邻居数$k$，并且获得的候选$Eps$参数可能不是唯一的。除了上述工作之外，还有一些工作[12,13]考虑了 DBSCAN与网格聚类相结合判断密度趋势，通过预先确定的网格划分参数根据每个数据区域的大小和形状来对原始样本聚类。虽然这些方法将参数选择的难度降低到一定程度，但在某种程度上，它们仍然需要用户至少启发式地决定一个参数，这是它们在数据有变化时不够灵活。

超参数优化：对于 DBSCAN 的参数， 另一种可行的参数决策方法是基于超参数优化（HO）算法。经典的 HO 方法是无模型方法，包括搜索所有可能参数地网格搜索以及随即搜索等。另一个 方法是贝叶斯优化方法，例如 BO-TPE[5]， SMAC[28]，它使用先前的经验优化搜索效率。 此外，元启发式优化方法，如 模拟退火[32]、遗传[36]、粒子群[46]和微分进化[45]，可以通过模拟物理、生物来解决非凸、非连续、非光滑优化问题，以实现搜索。基于元启发式优化算法，一些作品提出了DBSCAN的HO方法。 BDE-DBSCAN [30] 以外部纯度指数为目标，选择 参数基于二元差分进化算法来选择参数$MinPts$，使用一个竞赛选择算法来选择$Eps$参数。MOGA-DBSCAN[17]提出了异常指标作为目标函数地一种新的内部指标方法，并且基于一个多目标基因算法来选择参数。HO 方法避免了手工制作的启发式决策参数，它们 需要一个准确的目标函数（聚类外部/内部 指标）并且无法处理未标记数据的问题和 内部指标的误差。而 DRL-DBSCAN 不仅可以执行基于DBSCAN 的聚类状态感知参数搜索目标函数，还保留了学习到的搜索经验，并在没有目标函数的情况下也可以进行搜索。

**强化学习聚类：**最近有一些强化学习和聚类算法被提出。比如例粒子物理中的MCTS聚类[9]通过蒙特卡洛树搜索建立了高质量的多层聚类来从观测到的最终状态样本重建初始基本粒子。不过这些工作都是特定领域的强化学习聚类方法。与DRL-DBSCAN相比，它们建立的马尔可夫过程都只适用于特定任务，而不是一般的聚类方法。除了以上工作，[4]提出了一个提升后的K-Means聚类算法通过强化学习在不同维度选择距离度量的权重。但即使这个方法有效的提升了传统K-Means的表现，但它仍然需要提前决定类簇的数目$k$，这是一个巨大的限制。

6 结论

本篇文章，我们提出了一种基于深度强化学习的自适应DBSCAN参数搜索框架。在提出的框架中，通过感知聚类效果和状态来自适应调节参数搜索方向的智能体被用于与DBSCAN算法进行交互。我们设计递归机制建立多层结构以避免过大的参数空间带来性能损失。四种工作模式的实验结果证明提出的框架相比于基准线不仅在有标签数据上兼具准确性，稳定性和效率，还在无标签数据上依然保有有效的参数搜索能力。

参考文献：

[1] 2022. scikit-opt. https://github.com/guofei9987/scikit-opt
[2] Zohreh Akbari and Rainer Unland. 2016. Automated determination of the input parameter of DBSCAN based on outlier detection. In Ifip international conference on artificial intelligence applications and innovations. Springer, 280–291.
[3] Mihael Ankerst, Markus M Breunig, Hans-Peter Kriegel, and Jörg Sander. 1999. OPTICS: Ordering points to identify the clustering structure. ACM Sigmod record 28, 2 (1999), 49–60.
[4] Abraham Bagherjeiran, Christoph F Eick, and Ricardo Vilalta. 2005. Adaptive clustering: Better representatives with reinforcement learning. Department of Computer Science, University of Houston, Houston (2005).
[5] James Bergstra, Rémi Bardenet, Yoshua Bengio, and Balázs Kégl. 2011. Algorithms for hyper-parameter optimization. Advances in neural information processing systems 24 (2011).
[6] James Bergstra and Yoshua Bengio. 2012. Random search for hyper-parameter optimization. Journal of machine learning research 13, 2 (2012).
[7] James Bergstra, Daniel Yamins, and David Cox. 2013. Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures. In International conference on machine learning. PMLR, 115–123.
[8] Luuk Bom, Ruud Henken, and Marco Wiering. 2013. Reinforcement learning to train Ms. Pac-Man using higher-order action-relative inputs. In 2013 IEEE Symposium on Adaptive Dynamic Programming and Reinforcement Learning (ADPRL). IEEE, 156–163.
[9] Johann Brehmer, Sebastian Macaluso, Duccio Pappadopulo, and Kyle Cranmer.Hierarchical clustering in particle physics through reinforcement learning. arXiv preprint arXiv:2011.08191 (2020).
[10] Avory Bryant and Krzysztof Cios. 2017. RNN-DBSCAN: A density-based clustering algorithm using reverse nearest neighbor density estimates. IEEE Transactions on Knowledge and Data Engineering 30, 6 (2017), 1109–1121.
[11] Hong Chang and Dit-Yan Yeung. 2008. Robust path-based spectral clustering. Pattern Recognition 41, 1 (2008), 191–203.
[12] Huang Darong and Wang Peng. 2012. Grid-based DBSCAN algorithm with referential parameters. Physics Procedia 24 (2012), 1166–1170.
[13] Kejing Diao, Yongquan Liang, and Jiancong Fan. 2018. An improved DBSCAN algorithm using local parameters. In International CCF Conference on Artificial Intelligence. Springer, 3–12.
[14] Gabriel Dulac-Arnold, Richard Evans, Hado van Hasselt, Peter Sunehag, Timothy Lillicrap, Jonathan Hunt, Timothy Mann, TheophaneWeber, Thomas Degris, and Ben Coppin. 2015. Deep reinforcement learning in large discrete action spaces. arXiv preprint arXiv:1512.07679 (2015).
[15] Martin Ester, Hans-Peter Kriegel, Jörg Sander, Xiaowei Xu, et al. 1996. A densitybased algorithm for discovering clusters in large spatial databases with noise… In kdd, Vol. 96. 226–231.
[16] Pablo A Estévez, Michel Tesmer, Claudio A Perez, and Jacek M Zurada. 2009. Normalized mutual information feature selection. IEEE Transactions on neural networks 20, 2 (2009), 189–201.
[17] Zeinab Falahiazar, Alireza Bagheri, and Midia Reshadi. 2021. Determining the Parameters of DBSCAN Automatically Using the Multi-Objective Genetic Algorithm. J. Inf. Sci. Eng. 37, 1 (2021), 157–183.
[18] Tianhui Fan, Naijing Guo, and Yujie Ren. 2021. Consumer clusters detection with geo-tagged social network data using DBSCAN algorithm: a case study of the Pearl River Delta in China. GeoJournal 86, 1 (2021), 317–337.
[19] Z Fan and Xiaolong Xu. 2019. Application and visualization of typical clustering algorithms in seismic data analysis. Procedia Computer Science 151 (2019), 171–178.
[20] Ziad Francis, Carmen Villagrasa, and Isabelle Clairand. 2011. Simulation of DNA damage clustering after proton irradiation using an adapted DBSCAN algorithm. Computer methods and programs in biomedicine 101, 3 (2011), 265–270.
[21] Pasi Fränti and Sami Sieranoja. 2018. K-means properties on six clustering benchmark datasets. Applied intelligence 48, 12 (2018), 4743–4759.
[22] Scott Fujimoto, Herke Hoof, and David Meger. 2018. Addressing function approximation error in actor-critic methods. In International conference on machine learning. PMLR, 1587–1596.
[23] Aristides Gionis, Heikki Mannila, and Panayiotis Tsaparas. 2007. Clustering aggregation. Acm transactions on knowledge discovery from data (tkdd) 1, 1 (2007), 4–es.
[24] Eoin Martino Grua and Mark Hoogendoorn. 2018. Exploring clustering techniques for effective reinforcement learning based personalization for health and wellbeing. In 2018 IEEE Symposium Series on Computational Intelligence (SSCI). IEEE, 813–820.
[25] Chun Guan, Yuen Kevin Kam Fung, and Yong Yue. 2018. Towards a Personalized Item Recommendation Approach in Social Tagging Systems Using Intuitionistic Fuzzy DBSCAN. In 2018 10th International Conference on Intelligent Human- Machine Systems and Cybernetics (IHMSC), Vol. 1. IEEE, 361–364.
[26] Jian Hou, Huijun Gao, and Xuelong Li. 2016. DSets-DBSCAN: A parameterfree clustering algorithm. IEEE Transactions on Image Processing 25, 7 (2016), 3182–3193.

[27] Mengxing Huang, Qili Bao, Yu Zhang, and Wenlong Feng. 2019. A hybrid algorithm for forecasting financial time series data based on DBSCAN and SVR. Information 10, 3 (2019), 103.
[28] Frank Hutter, Holger H Hoos, and Kevin Leyton-Brown. 2011. Sequential modelbased optimization for general algorithm configuration. In International conference on learning and intelligent optimization. Springer, 507–523.
[29] Anssi Kanervisto, Christian Scheller, and Ville Hautamäki. 2020. Action space shaping in deep reinforcement learning. In 2020 IEEE Conference on Games (CoG). IEEE, 479–486.
[30] Amin Karami and Ronnie Johansson. 2014. Choosing DBSCAN parameters automatically using differential evolution. International Journal of Computer Applications 91, 7 (2014), 1–11.
[31] Mohammad Kazemi-Beydokhti, Rahim Ali Abbaspour, and Masoud Mojarab. Spatio-Temporal Modeling of Seismic Provinces of Iran Using DBSCAN Algorithm. Pure & Applied Geophysics 174, 5 (2017).
[32] Scott Kirkpatrick, C Daniel Gelatt Jr, and Mario P Vecchi. 1983. Optimization by simulated annealing. science 220, 4598 (1983), 671–680.
[33] Vijay R Konda and John N Tsitsiklis. 2000. Actor-critic algorithms. In Proceedings of the NIPS. 1008–1014.
[34] Urszula Kużelewska and Krzysztof Wichowski. 2015. A modified clustering algorithm DBSCAN used in a collaborative filtering recommender system for music recommendation. In International conference on dependability and complex systems. Springer, 245–254.
[35] Wenhao Lai, Mengran Zhou, Feng Hu, Kai Bian, and Qi Song. 2019. A new DBSCAN parameters determination method based on improved MVO. Ieee Access 7 (2019), 104085–104095.
[36] Stefan Lessmann, Robert Stahlbock, and Sven F Crone. 2005. Optimizing hyperparameters of support vector machines by genetic algorithms… In IC-AI. 74–82.
[37] Xinyan Li and Deren Li. 2007. Discovery of rules in urban public facility distribution based on DBSCAN clustering algorithm. In MIPPR 2007: Remote Sensing and GIS Data Processing and Applications; and Innovative Multispectral Technology and Applications, Vol. 6790. International Society for Optics and Photonics, 67902E.
[38] Timothy P Lillicrap, Jonathan J Hunt, Alexander Pritzel, Nicolas Heess, Tom Erez, Yuval Tassa, David Silver, and Daan Wierstra. 2015. Continuous control with deep reinforcement learning. arXiv preprint arXiv:1509.02971 (2015).
[39] Peng Liu, Dong Zhou, and Naijun Wu. 2007. VDBSCAN: varied density based spatial clustering of applications with noise. In 2007 International conference on service systems and service management. IEEE, 1–4.
[40] S. Mitra and Jay Nandy. 2011. KDDClus : A Simple Method for Multi-Density Clustering. In Proceedings of International Workshop on Soft Computing Applications and Knowledge Discovery (SCAKD). 72–76.
[41] Nwayyin Najat Mohammed, Micheal Cawthorne, and Adnan Mohsin Abdulazeez. Detection of Genes Patterns with an Enhanced Partitioning-Based DBSCAN Algorithm. Journal of information and communication engineering 4, 1 (2018),
188–195.
[42] Martin Mundhenk, Judy Goldsmith, Christopher Lusena, and Eric Allender. 2000. Complexity of finite-horizon Markov decision process problems. Journal of the ACM (JACM) 47, 4 (2000), 681–720.
[43] Michalis Pavlis, Les Dolega, and Alex Singleton. 2018. A modified DBSCAN clustering method to estimate retail center extent. Geographical Analysis 50, 2 (2018), 141–161.
[44] Hao Peng, Ruitong Zhang, Shaoning Li, Yuwei Cao, Shirui Pan, and Philip Yu. Reinforced, incremental and cross-lingual event detection from social messages. IEEE Transactions on Pattern Analysis and Machine Intelligence (2022).
[45] A Kai Qin, Vicky Ling Huang, and Ponnuthurai N Suganthan. 2008. Differential evolution algorithm with strategy adaptation for global numerical optimization. IEEE transactions on Evolutionary Computation 13, 2 (2008), 398–417.
[46] Yuhui Shi and Russell C Eberhart. 1998. Parameter selection in particle swarm optimization. In International conference on evolutionary programming. Springer, 591–600.
[47] Abir Smiti and Zied Elouedi. 2012. Dbscan-gm: An improved clustering method based on gaussian means and dbscan techniques. In 2012 IEEE 16th international conference on intelligent engineering systems (INES). IEEE, 573–578.
[48] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. 2017. Attention is all you need. Advances in neural information processing systems 30 (2017).
[49] Cor J. Veenman, Marcel J. T. Reinders, and Eric Backer. 2002. A maximum variance cluster algorithm. IEEE Transactions on pattern analysis and machine intelligence 24, 9 (2002), 1273–1280.
[50] Rahul Kumar Vijay and Satyasai Jagannath Nanda. 2019. A Variable -DBSCAN Algorithm for Declustering Earthquake Catalogs. In Soft Computing for Problem Solving. Springer, 639–651.
[51] Nguyen Xuan Vinh, Julien Epps, and James Bailey. 2010. Information theoretic measures for clusterings comparison: Variants, properties, normalization and correction for chance. JMLR 11 (2010), 2837–2854.
[52] Jiabin Wei et al. 2019. Commercial Activity Cluster Recognition with Modified DBSCAN Algorithm: A Case Study of Milan. In 2019 IEEE International Smart Cities Conference (ISC2). IEEE, 228–234.

[53] Li Yang and Abdallah Shami. 2020. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 415 (2020), 295–316.
[54] Yan Yang, Bin Lian, Lian Li, Chen Chen, and Pu Li. 2014. DBSCAN clustering algorithm applied to identify suspicious financial transactions. In 2014 International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery.
IEEE, 60–65.
[55] Charles T Zahn. 1971. Graph-theoretical methods for detecting and describing gestalt clusters. IEEE Transactions on computers 100, 1 (1971), 68–86.
[56] Kun Zheng, Husheng Li, Robert C Qiu, and Shuping Gong. 2012. Multi-objective reinforcement learning based routing in cognitive radio networks: Walking in a random maze. In 2012 international conference on computing, networking and communications (ICNC). IEEE, 359–363.
[57] Hong Bo Zhou and Jun Tao Gao. 2014. Automatic method for determining cluster number based on silhouette coefficient. In Advanced Materials Research, Vol. 951. Trans Tech Publ, 227–230.
2012 international conference on computing, networking and communications (ICNC). IEEE, 359–363.
[57] Hong Bo Zhou and Jun Tao Gao. 2014. Automatic method for determining cluster number based on silhouette coefficient. In Advanced Materials Research, Vol. 951. Trans Tech Publ, 227–230.
[58] X. Zhu. 2010. Stream Data Mining Repository. http://www.cse.fau.edu/~xqzhu/stream.html