GPS网的基线计算以及平差处理(使用Python绘制误差椭圆,C++处理数据并输出Qxx矩阵)
题目如下:
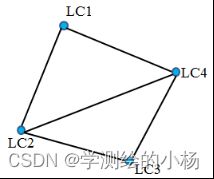
如下图所示为一简单GPS网,用两台GPS接收机观测,测得5条基线向量,每一条基线向量中三个坐标差观测值相关,由于只用两台GPS接收机观测,所以各观测基线向量互相独立。观测基线向量信息见表1。假定1号点为起算点坐标信息表2。
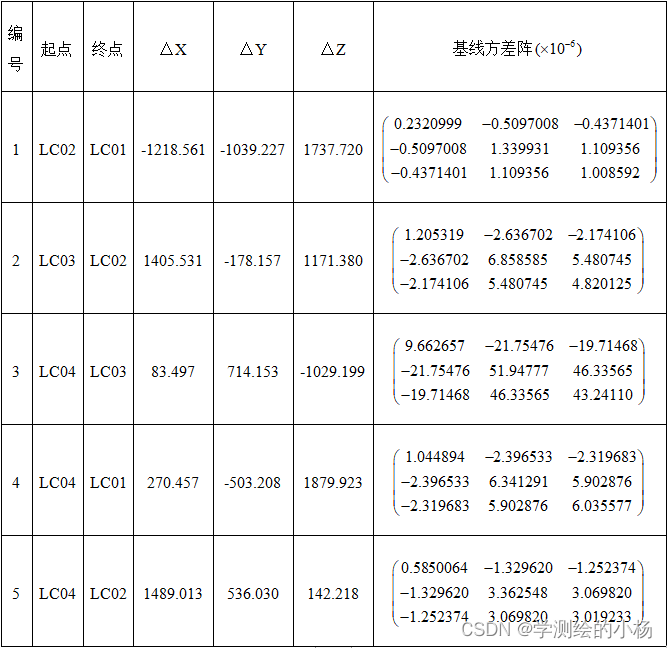
表1 GPS网平差观测数据及已知方差阵
表2 GPS网平差起算数据
| 点号 |
X |
Y |
Z |
| LC01 |
-1974638.7340 |
4590014.8190 |
3953144.9235 |
要求:1)基于Matlab或其他编程语言(如C++等)编程实现该GPS网间接平差过程通用程序,包括误差方程、法方程的组成与解算。得出平差后各基线向量观测值的平差值及各待定点的坐标平差值;评定各待定点坐标平差值的精度,绘制其误差椭圆。给出程序设计思路、流程图、程序代码和计算结果。
基本原理
1.间接平差方法
间接平差法是通过选定t个与观测值有一定关系的独立未知量作为参数,将每个观测值都分别表达成这t个参数的函数,建立函数模型,按最小二乘原理,用求函数极值的方法解出参数的最或然值,从而求得各观测值的平差值。
2.条件平差原理
程序实现:
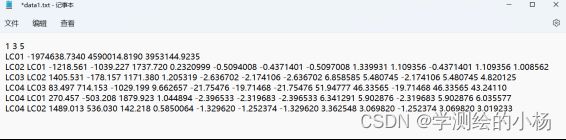
1.数据文件准备:
数据文件包括四个部分:文件头,已知点数据、基线数据和闭合环的序号(条件平差)
首先,文件头只有一行,并以空格或制表符隔开,包括已知点数量、未知点数量、基线数量。然后是已知点数据行数与头文件中已知点数量相同,每一行存储一个点的点名,X坐标、Y坐标和Z坐标,以空格或制表符隔开。最后是基线数据,其行数与头文件中基线数量相同,包含起点点名、终点点名、X坐标差、Y坐标差、Z坐标差和基线方差阵,以空格或制表符隔开。
间接平差文件结构设计如图:
2.程序设计结构(C++)
程序运行流程图
3.代码块讲解
1)新建了一个名为GPSnet.cpp的文件,其中包含Points结构体,GPSline结构体和一个GPSnet类,来存储GPS网相关数据和相关属性。
#include
#include
#include
#include 在GPSnet中存储了相应的代码进行运算,其中生成P阵的代码为
//读取基线数据,并计算出权阵P
for (int i = 0; i < observation_num; i++)
{
ifs >> lines[i].begin.pointName >> lines[i].end.pointName
>> lines[i].dx >> lines[i].dy >> lines[i].dz;
lines[i].begin.known = false;
lines[i].end.known = false;
ifs >> P(i * 3 + 0, i * 3 + 0) >> P(i * 3 + 0, i * 3 + 1) >> P(i * 3 + 0, i * 3 + 2)
>> P(i * 3 + 1, i * 3 + 0) >> P(i * 3 + 1, i * 3 + 1) >> P(i * 3 + 1, i * 3 + 2)
>> P(i * 3 + 2, i * 3 + 0) >> P(i * 3 + 2, i * 3 + 1) >> P(i * 3 + 2, i * 3 + 2);
}生成B阵的代码为:
//计算每个点的近似坐标
while (true)
{
//循环结束标志,初值为true,若该次循环没有计算近似坐标,循环结束
bool success = true;
for (int i = 0; i < observation_num; i++)
{
//第一种情况:起点坐标已知,终点未知,则终点坐标=起点坐标+(deltax,deltay,deltaz)
if (lines[i].begin.known == true && lines[i].end.known == false)
{
lines[i].end.x = lines[i].begin.x + lines[i].dx;//赋值
lines[i].end.y = lines[i].begin.y + lines[i].dy;
lines[i].end.z = lines[i].begin.z + lines[i].dz;
//为GPS网络中,所有与该终点名称相同的点赋值
for (int j = 0; j < observation_num; j++)
{
if (lines[j].end.pointName == lines[i].end.pointName)
{
lines[j].end.known = true;//赋为已知点
lines[j].end.pointNum = lines[i].end.pointNum;//赋值点号
lines[j].end.x = lines[i].end.x;
lines[j].end.y = lines[i].end.y;
lines[j].end.z = lines[i].end.z;
}
if (lines[j].begin.pointName == lines[i].end.pointName)
{
lines[j].begin.known = true;
lines[j].begin.pointNum = lines[i].end.pointNum;
lines[j].begin.x = lines[i].end.x;
lines[j].begin.y = lines[i].end.y;
lines[j].begin.z = lines[i].end.z;
}
}
lines[i].end.known = true;//判断其是否已经接受过处理
success = false;
}
//第二种情况:起点坐标未知,终点已知,计算相关的近似坐标,两个过程相似,复制粘贴后进行相关整理
if (lines[i].begin.known == false && lines[i].end.known == true)
{
//为起点坐标赋值
lines[i].begin.x = lines[i].end.x - lines[i].dx;
lines[i].begin.y = lines[i].end.y - lines[i].dy;
lines[i].begin.z = lines[i].end.z - lines[i].dz;
//为GPS网络中,所有与该起点名称相同的点赋值
for (int j = 0; j < observation_num; j++)
{
if (lines[j].begin.pointName == lines[i].begin.pointName)
{
lines[j].begin.known = true;
lines[j].begin.pointNum = lines[i].begin.pointNum;
lines[j].begin.x = lines[i].begin.x;
lines[j].begin.y = lines[i].begin.y;
lines[j].begin.z = lines[i].begin.z;//与上述内容类似
}
if (lines[j].end.pointName == lines[i].begin.pointName)
{
lines[j].end.known = true;
lines[j].end.pointNum = lines[i].begin.pointNum;
lines[j].end.x = lines[i].begin.x;
lines[j].end.y = lines[i].begin.y;
lines[j].end.z = lines[i].begin.z;
}
}
lines[i].begin.known = true;
success = false;
}
}
if (success == true)
break;//当以上过程结束,将会结束循环
}
//计算b、l矩阵
for (int i = 0; i < observation_num; i++)
{
int beginIndex = lines[i].begin.pointNum - (known_point_num - 1) - 1;//设置开始点号的index
int endIndex = lines[i].end.pointNum - (known_point_num - 1) - 1;//设置结束点好的index
if (beginIndex >= 0)//当其发现起始点index为正数时,给矩阵相关元素赋值-1
{
B(3 * i + 0, 3 * beginIndex + 0) = -1;
B(3 * i + 1, 3 * beginIndex + 1) = -1;
B(3 * i + 2, 3 * beginIndex + 2) = -1;
}
if (endIndex >= 0)//当其发现终点index为正数时,给矩阵相关元素赋值1
{
B(3 * i + 0, 3 * endIndex + 0) = 1;
B(3 * i + 1, 3 * endIndex + 1) = 1;
B(3 * i + 2, 3 * endIndex + 2) = 1;
}
l(3 * i + 0, 0) = lines[i].dx - (lines[i].end.x - lines[i].begin.x);//给l赋值,组成l阵
l(3 * i + 1, 0) = lines[i].dy - (lines[i].end.y - lines[i].begin.y);//观测值减去近似坐标的值为l阵
l(3 * i + 2, 0) = lines[i].dz - (lines[i].end.z - lines[i].begin.z);
}
x = (B.transpose() * P * B).inverse() * B.transpose() * P * l;
v = B * x - l;
}输出控制台函数为:
//输出解算结果到控制台
void GPSnet::print()
{
MatrixXd Qxx = (B.transpose() * P * B).inverse();
cout << "*******************平差结果*******************" << endl;
cout << "P:" << endl << P << endl;
cout << "B:" << endl << B << endl;
cout << "l:" << endl << l << endl;
cout << "x:" << endl << x << endl;
cout << "v:" << endl << v << endl;
cout << "观测值平差值"<将Nbb阵放入文件方法代码如下:
void GPSnet::calculation() {
ofstream ofs1;//新建文件输出流
ofs1.open("./Qxx&sigma output.txt", ios::out);
MatrixXd Qxx = (B.transpose() * P * B).inverse();//计算Qxx阵,方便元素取出
double sigma = sqrt((v.transpose() * P * v)(0, 0) / 3);//单位权中误差获取
ofs1 << nuknown_point_num << endl ;//取出未知点
ofs1 << sigma << endl;//取出单位权中误差
for (int i = 0; i < 3 * nuknown_point_num; i++) {
for (int j = 0; j < 3 * nuknown_point_num; j++) {
if (j != 3 * nuknown_point_num - 1) {
ofs1 << Qxx(i, j) << " ";//取出所有元素,以方阵的形式取出,并写入到文件中,在main.py处绘制误差椭圆
}
else {
ofs1 << Qxx(i, j) << endl;//取出元素
}
}
}
}完整代码如下:
//作者:Henry Yang
//山东科技大学
//测量平差课程设计之GPS网平差通用程序
//ver1.0.1
#include
#include
#include
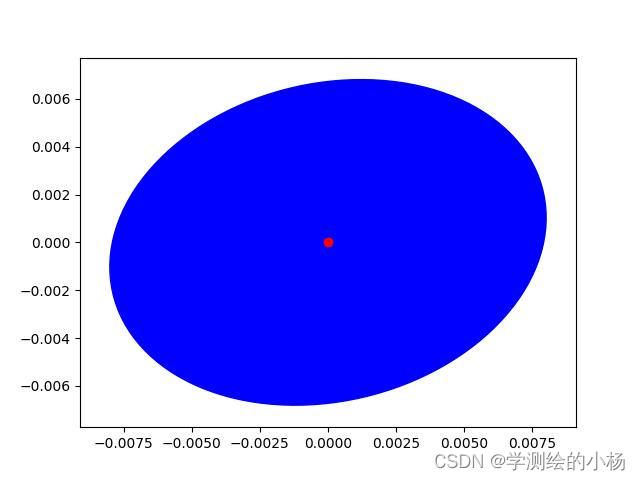
#include 绘制误差椭圆(Python实现)
该程序使用C++生成的结果,绘制误差椭圆,使用numpy和matplotlib,绘制相关图。
import math
from matplotlib.patches import Ellipse
import matplotlib.pyplot as plt
import numpy as np
file = open("GPSnet\\test\\Qxx&sigma output.txt", "r")# 读取权阵和单位权中误差
unknown_points_num = int(file.readline())
sigma = float(file.readline())#获得单位权中误差
Qxx = []
for i in range(0, 3 * unknown_points_num):
arr = []
arr = file.readline().split(" ")
arr1 = [x.strip() for x in arr if x.strip() != '\n'] # 去掉读取中产生的换行符
arr2 = [float(x) for x in arr1]
Qxx.append(arr2)
MatQxx = np.mat(Qxx) # 生成矩阵
j = 0
for i in range(0, unknown_points_num):
cut = np.zeros((3, 3))
cut = MatQxx[i + j:i + j + 2, i + j:i + j + 2]#将矩阵分块
j = j + 2
Qxx = float(cut[0, 0])#矩阵重新赋值
Qyy = float(cut[1, 1])
Qxy = float(cut[0, 1])
fi = math.atan(2 * Qxy / (Qxx - Qyy)) / 2
E = 0.5 * pow(sigma, 2) * (Qxx + Qyy + math.sqrt(pow(Qxx - Qyy, 2) + 4 * pow(Qxy, 2)))#计算最大最小值
F = 0.5 * pow(sigma, 2) * (Qxx + Qyy + math.sqrt(pow(Qxx - Qyy, 2) - 4 * pow(Qxy, 2)))
fig = plt.figure()#创建plt对象
ax = fig.add_subplot(111)
print(math.degrees(fi))
ell1 = Ellipse(xy=(0.0, 0.0), width=2 * math.sqrt(E), height=2 * math.sqrt(F), angle=math.degrees(fi),color="blue")#绘制椭圆 长半轴 短半轴设置,设置偏移角度,换算成角度值(degrees)
ax.add_patch(ell1)#在图中添加椭圆对象
x, y = 0, 0#设置坐标轴坐标
ax.plot(x, y, 'ro')
plt.savefig("{}.jpg".format(i))#存储到根目录中得到结果如下:
学习不易,如有转载,请与作者联系。