卷积神经网络CNN详解
一、全连接神经网络
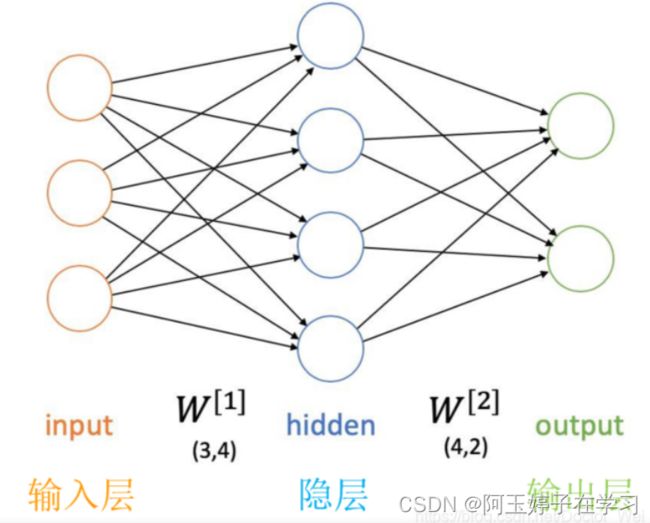
1、全连接网络:网络层的每一个结点都与上一层的所有结点相连。
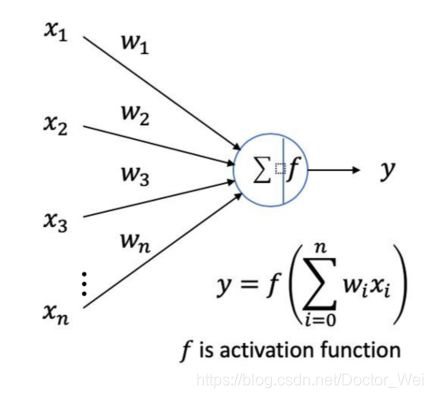
对于每个神经元:
2、如果没有激活函数,我们的求和函数拟合能力均为线性的,而激活函数的作用在于,为我们的模型提供了非线性的拟合能力。
2.1 全连接神经网络_小学渣的春天的博客-CSDN博客_一个全连接的前向神经网络具有6个源结点,2个隐层2.1 全连接神经网络2.1.1 全连接神经网络的定义全连接网络:网络层的每一个结点都与上一层的所有结点相连。2.1.2 对于每一个神经元每一个神经元都可以分为两部分:求和函数、激活函数部分1:求和函数z=w1Tx1+w2Tx2+⋯+wnTxnz=w_1^{\rm T}x_1+w_2^{\rm T}x_2+\cdots+w_n^{\rm T}x_nz=w1Tx1+w2Tx2+⋯+wnTxn2:激活函数y=f(z)y=f(z)y=f(z)2.1.3 激活函数带来了什么?如果https://blog.csdn.net/Doctor_Wei/article/details/109597113?spm=1001.2101.3001.6650.1&utm_medium=distribute.pc_relevant.none-task-blog-2~default~CTRLIST~default-1.pc_relevant_default&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2~default~CTRLIST~default-1.pc_relevant_default&utm_relevant_index=2
3、全连接神经网络处理大尺寸图像具有三个明显的缺点:
(1)首先将图像展开为向量会丢失空间信息;
(2)其次参数过多效率低下,训练困难;
(3)同时大量的参数也很快会导致网络过拟合。
而使用卷积神经网络可以很好地解决上面的三个问题。
二、卷积神经网络
与常规神经网络不同,卷积神经网络的各层中的神经元是3维排列的:宽度、高度和深度。
其中的宽度和高度是很好理解的,因为本身卷积就是一个二维模板,但是在卷积神经网络中的深度指的是网络的层数。
举个例子来理解什么是宽度,高度和深度,假如使用CIFAR-10中的图像是作为卷积神经网络的输入,该输入数据体的维度是32x32x3(宽度,高度和深度)。我们将看到,层中的神经元将只与前一层中的一小块区域连接,而不是采取全连接方式。
对于用来分类CIFAR-10中的图像的卷积网络,其最后的输出层的维度是1x1x10,因为在卷积神经网络结构的最后部分将会把全尺寸的图像压缩为包含分类评分的一个向量,向量是在深度方向排列的。下面是例子:
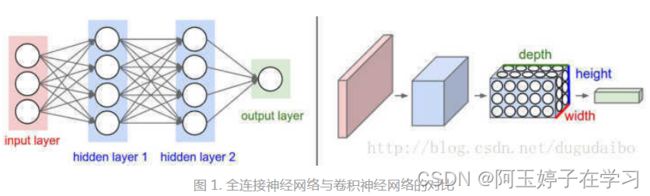
左侧是一个3层的神经网络(输入层、中间隐藏层、输出层);
右侧是一个卷积神经网络,将它的神经元在成3个维度(宽、高、深度)进行排列;红色的输入层代表输入图像,所以它的宽度和高度就是图像的宽度和高度,它的深度是3(代表了红、绿、蓝3种颜色通道),与红色相邻的蓝色部分是经过卷积和池化之后的激活值(也可以看做是神经元) ,后面是接着的卷积池化层。
卷积神经网络的每一层都将3D的输入数据变化为神经元3D的激活数据并输出;
三、卷积神经网络的各种层
卷积神经网络主要由这几类构成:输入层、卷积层,ReLU层、池化层和全连接层(全连接层和常规神经网络中的一样)。将这些层叠加起来,就可以构建一个完整的卷积神经网络。
在实际应用中往往将卷积层与ReLU层共同称之为卷积层,所以卷积层经过卷积操作也是要经过激活函数的。具体说来,卷积层和全连接层(CONV/FC)对输入执行变换操作的时候,不仅会用到激活函数,还会用到很多参数,即神经元的权值w和偏差b;而ReLU层和池化层则是进行一个固定不变的函数操作。卷积层和全连接层中的参数会随着梯度下降被训练,这样卷积神经网络计算出的分类评分就能和训练集中的每个图像的标签吻合了。
1、卷积层
卷积层是构建卷积神经网络的核心层,产生了网络中大部分的计算量。注意计算量而不是参数量。
2、卷积层作用
- 滤波器的作用或者说是卷积的作用。卷积层的参数是由一些可学习的滤波器集合构成的。每个滤波器在空间上(宽度和高度)都比较小,但是深度和输入数据一致(这一点很重要,后面会具体介绍)。直观地来说,网络会让滤波器学习到当它看到某些类型的视觉特征时就激活,具体的视觉特征可能是某些方位上的边界,或者在第一层上某些颜色的斑点,甚至可以是网络更高层上的蜂巢状或者车轮状图案。
- 可以被看做是神经元的一个输出。神经元只观察输入数据中的一小部分,并且和空间上左右两边的所有神经元共享参数(因为这些数字都是使用同一个滤波器得到的结果)。
- 降低参数的数量。这个由于卷积具有“权值共享”这样的特性,可以降低参数数量,达到降低计算开销,防止由于参数过多而造成过拟合。
3、感受野(重点)
在处理图像的高维度输入时,让每个神经元都与前一层中的所有神经元进行全连接是不现实的。
相反,我们让每个神经元只与输入数据的一个局部区域连接。该连接的空间大小叫做神经元的感受野(receptive field),它的尺寸是一个超参数(其实就是滤波器的空间尺寸)。
在深度方向上,这个连接的大小总是和输入量的深度相等。需要再次强调的是,我们对待空间维度(宽和高)与深度维度是不同的,但是在深度上总是和输入数据的深度一致,这一点会在下面举例具体说明。
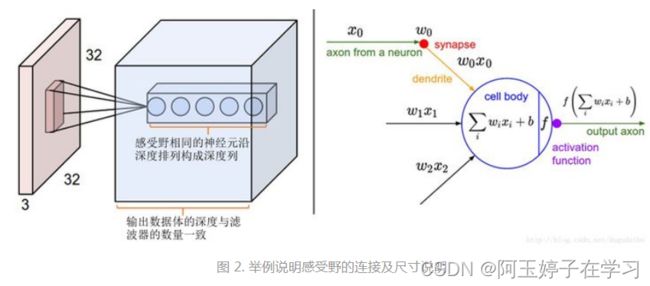
在图 2 中展现的卷积神经网络的一部分,其中的红色为输入数据,假设输入数据体尺寸为[32x32x3](比如CIFAR-10的RGB图像),如果感受野(或滤波器尺寸)是5x5,那么卷积层中的每个神经元会有输入数据体中[5x5x3]区域的权重,共5x5x3=75个权重(还要加一个偏差参数)。
注意这个连接在深度维度上的大小必须为3,和输入数据体的深度一致。
其中还有一点需要注意,对应一个感受野有75个权重,这75个权重是通过学习进行更新的,所以很大程度上这些权值之间是不相等。
注意是一个偏置,无论输入输入数据是多少层,一个卷积核就对应一个偏置。
4、神经元的空间排列
感受野讲解了卷积层中每个神经元与输入数据体之间的连接方式,但是尚未讨论输出数据体中神经元的数量,以及它们的排列方式。
3个超参数控制着输出数据体的尺寸:深度,步长和零填充。
(1) 输出数据体的深度:它是一个超参数,和使用的滤波器的数量一致,而每个滤波器在输入数据中寻找一些不同的东西,即图像的某些特征。(注意图像的深度和输出的深度不同?)
(2) 在滑动滤波器的时候,必须指定步长。当步长为1,滤波器每次移动1个像素;当步长为2,滤波器滑动时每次移动2个像素,当然步长也可以是不常用的3,或者更大的数字,但这些在实际中很少使用)。这个操作会让输出数据体在空间上变小。
(3) 有时候将输入数据体用0在边缘处进行填充是很方便的。这个零填充(zero-padding)的尺寸是一个超参数。零填充有一个良好性质,即可以控制输出数据体的空间尺寸(最常用的是用来保持输入数据体在空间上的尺寸,使得输入和输出的宽高都相等)。
5、权值共享
在卷积层中权值共享是用来控制参数的数量。假如在一个卷积核中,每一个感受野采用的都是不同的权重值(卷积核的值不同),那么这样的网络中参数数量将是十分巨大的。
权值共享是基于这样的一个合理的假设:如果一个特征在计算某个空间位置 (x1,y1)(x1,y1) 的时候有用,那么它在计算另一个不同位置 (x2,y2)(x2,y2) 的时候也有用。
比如一个数据体尺寸为[55x55x96]的就有96个深度切片,每个尺寸为[55x55],其中在每个深度切片上的结果都使用同样的权重和偏差获得的。在这样的参数共享下,假如卷积层有96个卷积核,那么就有96个不同的权重集了,一个权重集对应一个深度切片,如果卷积核的大小是 11x11的,图像是RGB 3 通道的,那么就共有96x11x11x3=34,848个不同的权重,总共有34,944个参数(因为要+96个偏差),且在每个深度切片中的55x55 的结果使用都是同样的参数。
在反向传播的时候,都要计算每个神经元对它的权重的梯度,但是需要把同一个深度切片上的所有神经元对权重的梯度累加,这样就得到了对共享权重的梯度。这样,每个切片只更新一个权重集。这样做的原因可以通过下面这张图进行解释。
而每个切片只更新一个权重集的原因也是这样的,从图3 中可以看到,不同深度的神经元不会公用相同的权重,所以只能更新一个权重集。
注意:
如果在一个深度切片中的所有权重都使用同一个权重向量,那么卷积层的前向传播在每个深度切片中可以看做是在计算神经元权重和输入数据体的卷积(这就是“卷积层”名字由来)。这也是为什么总是将这些权重集合称为滤波器(filter)或卷积核(kernel),因为它们和输入进行了卷积。
有时候参数共享假设可能没有意义!特别是当卷积神经网络的输入图像是一些明确的中心结构时候。这时候我们就应该期望在图片的不同位置学习到完全不同的特征(而一个卷积核滑动地与图像做卷积都是在学习相同的特征)。
一个具体的例子就是输入图像是人脸,人脸一般都处于图片中心,而我们期望在不同的位置学习到不同的特征,比如眼睛特征或者头发特征可能(也应该)会在图片的不同位置被学习。在这个例子中,通常就放松参数共享的限制,将层称为局部连接层(Locally-Connected Layer)。
6、卷积层的超参数及选择
对这些超参数,常见的设置是 F=3,S=1,P=1。同时设置这些超参数也有一些约定俗成的惯例和经验,可以在下面的“卷积神经网络结构”中查看。
其中:感受野尺寸(F),步长(S),滤波器数量(K),零填充的数量(P),通道数(D)。
7、卷积层演示
所有的数据(输入数据体是蓝色,权重数据体是红色,输出数据体是绿色)都采取将深度切片按列的方式排列展现。
输入数据体的尺寸是W1=5,H1=5,D1=3,卷积层参数K=2,F=3,S=2,P=1。就是说,有2个滤波器,滤波器的尺寸是3⋅3⋅3,它们的步长是2。
因此,输出数据体的空间尺寸是(5−3+2)/2+1=3、(5−3+2)/2+1=3。
注意输入数据体使用了零填充P=1,所以输入数据体外边缘一圈都是0。
每个元素都是先通过蓝色的输入数据和红色的滤波器逐元素相乘,然后求其总和,最后加上偏差。
8、用矩阵乘法实现卷积
卷积运算本质上就是在滤波器和输入数据的局部区域间做点积。
卷积层的常用实现方式将卷积层的前向传播变成一个巨大的矩阵乘法。
比如输入是[227x227x3],要与尺寸为11x11x3的滤波器以步长为4进行卷积,就依次取输入中的[11x11x3]数据块,然后将其拉伸为长度为11x11x3=363的列向量。重复进行这一过程,因为步长为4,所以经过卷积后的宽和高均为(227-11)/4+1=55,共有55x55=3,025个个神经元。因为每一个神经元实际上都是对应有 363 的列向量构成的感受野,即一共要从输入上取出 3025 个 363 维的列向量。所以得到的输出矩阵的尺寸是[363x3025],其中每列是拉伸的感受野。注意因为感受野之间有重叠,所以输入数据体中的数字在不同的列中可能有重复。
9、其他形式的卷积操作
1x1卷积:因为信号是2维的,所以1x1卷积就没有意义。但是,在卷积神经网络中不是这样,因为这里是对3个维度进行操作,滤波器和输入数据体的深度是一样的。比如,如果输入是[32x32x3],那么1x1卷积就是在高效地进行3维点积(因为输入深度是3个通道);另外的一种想法是将这种卷积的结果看作是全连接层的一种实现方式。
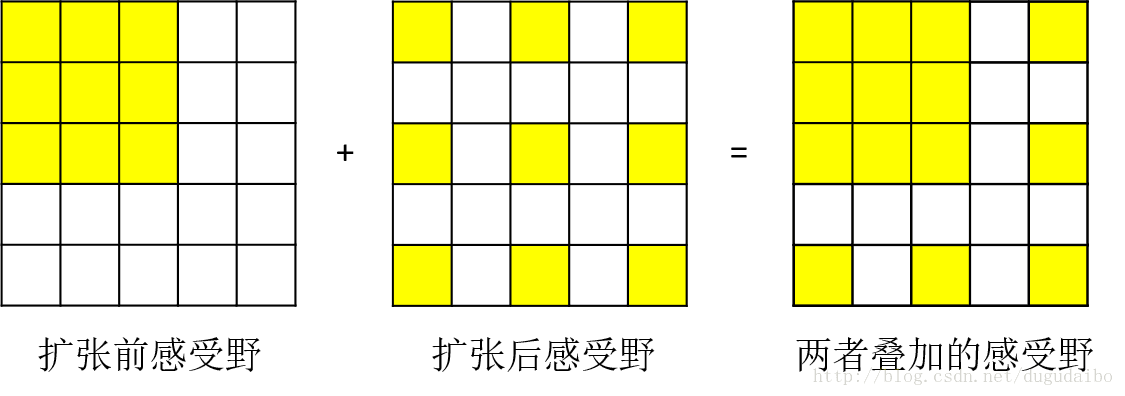
扩张卷积:到目前为止,我们只讨论了卷积层滤波器是连续的情况。但是,让滤波器中元素之间有间隙也是可以的,这就叫做扩张。
在某些设置中,扩张卷积与正常卷积结合起来非常有用,因为在很少的层数内更快地汇集输入图片的大尺度特征。
1、池化层
通常在连续的卷积层之间会周期性地插入一个池化层。它的作用是逐渐降低数据体的空间尺寸,这样的话就能减少网络中参数的数量,使得计算资源耗费变少,也能有效控制过拟合。
例如汇聚层使用 MAX 操作,对输入数据体的每一个深度切片独立进行操作,改变它的空间尺寸。最常见的形式是汇聚层使用尺寸2x2的滤波器,以步长为2来对每个深度切片进行降采样,将其中75%的激活信息都丢掉。每个MAX操作是从4个数字中取最大值(也就是在深度切片中某个2x2的区域),而且深度保持不变。
在实践中,最大池化层通常只有两种形式:一种是F=3,S=2,也叫重叠汇聚,另一个更常用的是F=2,S=2。对更大感受野进行池化需要的池化尺寸也更大,而且往往对网络有破坏性。
- 普通池化(General Pooling):除了最大池化,池化单元还可以使用其他的函数,比如平均池化(average pooling)或L-2范式池化(L2-norm pooling)。平均池化历史上比较常用,但是现在已经很少使用了。因为实践证明,最大池化的效果比平均池化要好。
- 反向传播:回顾一下反向传播的内容,其中max(x,y)函数的反向传播可以简单理解为将梯度只沿最大的数回传。因此,在向前传播经过汇聚层的时候,通常会把池中最大元素的索引记录下来(有时这个也叫作道岔(switches)),这样在反向传播的时候梯度的路由就很高效。
- 不使用汇聚层:很多人不喜欢汇聚操作,认为可以不使用它。抛弃汇聚层。通过在卷积层中使用更大的步长来降低数据体的尺寸。有发现认为,在训练一个良好的生成模型时,弃用汇聚层也是很重要的。比如变化自编码器(VAEs:variational autoencoders)和生成性对抗网络(GANs:generative adversarial networks)。现在看起来,未来的卷积网络结构中,可能会很少使用甚至不使用汇聚层。
1、全连接层
这个常规神经网络中一样,它们的激活可以先用矩阵乘法,再加上偏差。
2、将卷积层转化成全连接层
对于任一个卷积层,都存在一个能实现和它一样的前向传播函数的全连接层。
该全连接层的权重是一个巨大的矩阵,除了某些特定块(感受野),其余部分都是零;而在非 0 部分中,大部分元素都是相等的(权值共享),具体可以参考图3。
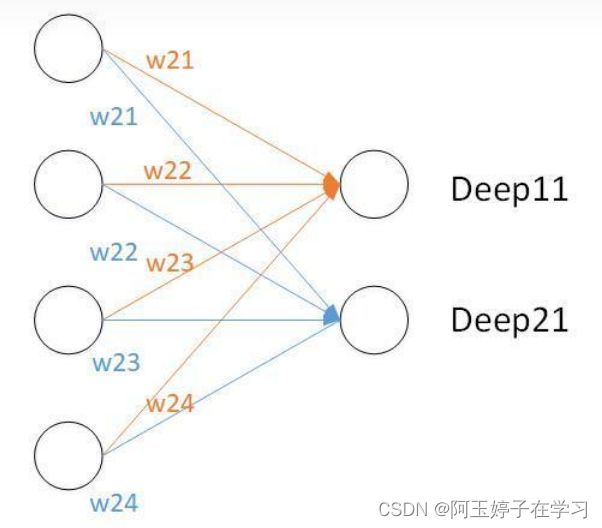
如果把全连接层转化成卷积层,以输出层的 Deep11 为例,与它有关的输入神经元只有上面四个,所以在权重矩阵中与它相乘的元素,除了它所对应的4个,剩下的均为0,这也就解释了为什么权重矩阵中有为零的部分;
另外要把“将全连接层转化成卷积层”和“用矩阵乘法实现卷积”区别开,这两者是不同的,后者本身还是在计算卷积,只不过将其展开为矩阵相乘的形式,并不是”将全连接层转化成卷积层”,所以除非权重中本身有零,否则用矩阵乘法实现卷积的过程中不会出现值为0的权重!!!
3、将全连接层转化成卷积层
任何全连接层都可以被转化为卷积层。
比如,一个K=4096的全连接层,输入数据体的尺寸是 7×7×512,这个全连接层可以被等效地看做一个F=7,P=0,S=1,K=4096的卷积层。
换句话说,就是将滤波器的尺寸设置为和输入数据体的尺寸设为一致的。因为只有一个单独的深度列覆盖并滑过输入数据体,所以输出将变成1×1×40961×1×4096,这个结果就和使用初始的那个全连接层一样了。这个实际上也很好理解,因为,对于其中的一个卷积滤波器,这个滤波器的的深度为512,也就是说,虽然这个卷积滤波器的输出只有1个,但是它的权重有7×7×512,相当于卷积滤波器的输出为一个神经元,这个神经元与上一层的所有神经元相连接,而这样与前一层所有神经元相连接的神经元一共有4096个,这不就是一个全连接网络嘛~
在上述的两种变换中,将全连接层转化为卷积层在实际运用中更加有用。假设一个卷积神经网络的输入是224x224x3的图像,一系列的卷积层和汇聚层将图像数据变为尺寸为7x7x512的激活数据体(在AlexNet中就是这样,通过使用5个汇聚层来对输入数据进行空间上的降采样,每次尺寸下降一半,所以最终空间尺寸为224/2/2/2/2/2=7)。从这里可以看到,AlexNet使用了两个尺寸为4096的全连接层,最后一个有1000个神经元的全连接层用于计算分类评分。
假设原始图像的大小为 4×4,卷积核 F=3,S=1,P=1,而较大的图像的尺寸为 8×8,假设对图像进行两层的卷积池化,在较大的图像上以步长为4进行滑动,如图5所示:
对原始图像(图5左图红框)进行卷积得到的结果是图5右图红色框内的结果,使用步长为4在较大的图像获得的结果为图5中右侧四种颜色加在一起的样子。
所以以步长为4在8x8的图片上滑动,把每个经停的位置都带入卷积网络,最后得到2x2个位置的卷积结果,但是如果直接使用卷积核 F=3,S=1,P=1进行两次卷积池化的话,得到的结果的大小显然也是4×4的。
所以从获得结果来看,这两者是相同的,但是不同点在哪呢?
小节
(1) 用一整图像进行卷积和在较大的图像上通过滑动窗提取出一个个子图象进行卷积得到的效果是相同的。
(2) 可以这样做的主要原因在于将最后的全连接层改写成了卷积层。
(3) 在一整图像做卷积的效率要远远高于在图像上滑动的效率,因为前者只需要一次前向传播,而后者需要多次
(4) 用整张图像计算与滑动窗口的方法对比,所补充的零更少(如上所讲,不用零而是用在其旁边的像素代替),提取的信息损失的更少。
用整张图像计算卷积不仅在效率上高于滑动窗口的方法,而且更多的保留了图像的细节,完胜!
卷积层的大小选择
几个小滤波器卷积层的组合比一个大滤波器卷积层好。
假设所有的数据有C个通道,那么单独的7x7卷积层将会包含 49C^2个参数,而3个3x3的卷积层的组合仅有 27C^2个参数。
层的尺寸设置规律
- 输入层 ,应该能被2整除很多次。常用数字包括32(比如CIFAR-10),64,96(比如STL-10)或224(比如ImageNet卷积神经网络),384和512。
- 卷积层 ,应该使用小尺寸滤波器(比如3x3或最多5x5),使用步长S=1。还有一点非常重要,就是对输入数据进行零填充,这样卷积层就不会改变输入数据在空间维度上的尺寸。比如,当F=3,那就使用P=1来保持输入尺寸。当F=5,P=2,一般对于任意F,当P=(F-1)/2的时候能保持输入尺寸。如果必须使用更大的滤波器尺寸(比如7x7之类),通常只用在第一个面对原始图像的卷积层上。
- 汇聚层 ,负责对输入数据的空间维度进行降采样。最常用的设置是用用2x2感受野(即F=2)的最大值汇聚,步长为2(S=2)。注意这一操作将会把输入数据中75%的激活数据丢弃(因为对宽度和高度都进行了2的降采样)。另一个不那么常用的设置是使用3x3的感受野,步长为2。最大值汇聚的感受野尺寸很少有超过3的,因为汇聚操作过于激烈,易造成数据信息丢失,这通常会导致算法性能变差。
为何使用零填充?使用零填充除了前面提到的可以让卷积层的输出数据保持和输入数据在空间维度的不变,还可以提高算法性能。如果卷积层值进行卷积而不进行零填充,那么数据体的尺寸就会略微减小,那么图像边缘的信息就会过快地损失掉。
因为内存限制所做的妥协:在某些案例(尤其是早期的卷积神经网络结构)中,基于前面的各种规则,内存的使用量迅速飙升。例如,使用64个尺寸为3x3的滤波器对224x224x3的图像进行卷积,零填充为1,得到的激活数据体尺寸是[224x224x64]。这个数量就是一千万的激活数据,或者就是72MB的内存(每张图就是这么多,激活函数和梯度都是)。因为GPU通常因为内存导致性能瓶颈,所以做出一些妥协是必须的。在实践中,人们倾向于在网络的第一个卷积层做出妥协。例如,可以妥协可能是在第一个卷积层使用步长为2,尺寸为7x7的滤波器(比如在ZFnet中)。在AlexNet中,滤波器的尺寸的11x11,步长为4。