第12章 Stata非线性回归分析
目录
12.1非参数回归分析
案例延伸
延伸1：设定散点图被分成垂直等宽波段的数量
延伸2：设定修匀的波段宽度
12.2转换变量回归分析
12.3非线性回归
案例延伸
延伸1：设定非线性回归模型中被估计参数的初始值
延伸2：采用文件的标准差进行非线性回归估计
延伸3：采用系统默认快捷函数进行非线性回归
前面讲述的回归分析方法都属于线性回归的范畴，即因变量和自变量之间存在线性关系。在很多情况下，线性模型都是对真实情况的一种合理又简单的近似。如果遇到回归参数不是现行的，也不能通过转换的方法将其转换为线性的参数，这时候就需要用到本章将要讲述的非线性回归分析。常用的非线性分析方法由3终，包括非参数回归分析、转换变量回归分析以及非线性回归分析。
12.1非参数回归分析
非参数回归分析与前面讲述的回归方式区别很大，是一种探索性工具，通常不会像其他回归方法一样形成一个明确的回归方程，基本上是展示因变量与自变量之间关系的图形工具。其优势在于不要求研究者事先设定模型的情况下就可直观概要的描述数据。
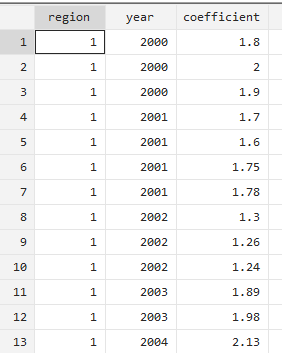
数据（案例12.1）是某国内保险公司采取区域事业部制的组织机构模式，在国内有两个事业部；北方事业部和南方事业部。该公司对其客户经理制定了了严格的激励约束措施，可交互精力的薪酬为基本工资乘以绩效考核系数，绩效考核系数上不封顶、下不保底，所以客户精力之间的收入差距很大。某研究者随机抽取的部分客户经理的理念考核系数如下图，请用非参数回归方法研究年份和绩效考核系数两个变量之间的关系。把所属事业部变量设定为region 年份为year 考核系数为coefficient
sum year coefficient,detail #对两个变量进行描述性统计
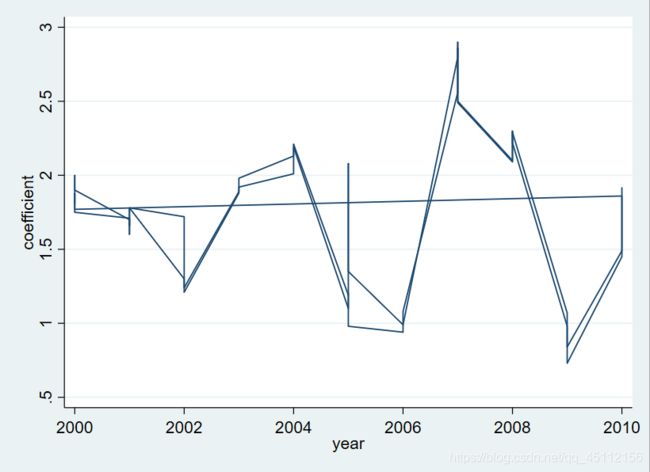
twoway line coefficient year #描述年份和绩效考核系数之间的变化关系，用绘图功能表示
我们可以看出使用普通的绘图方式来藐视年份和绩效考核系数之间的变化关系是非常不清晰的，所以很有必要进行非参数回归来描述这种关系。
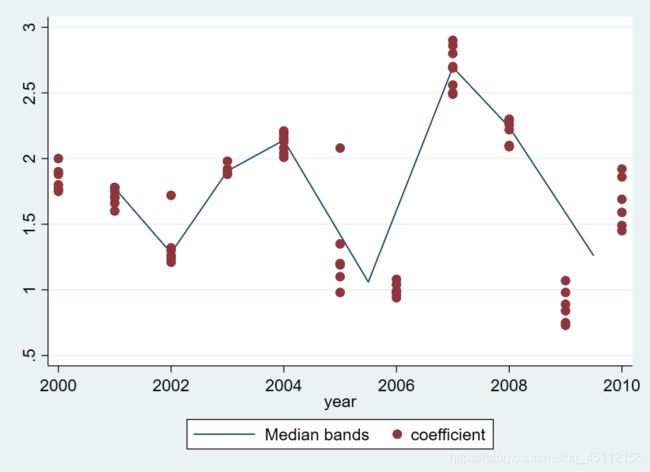
graph twoway mband coefficient year || scatter coefficient year #本命令是对数据进行非参数回归并绘制年份和绩效考核系数之间的散点图
从图中可以看出散点图被分成了8个垂直等宽的波段，并使用线段将每一波段内的中位数（年份的中位数、绩效考核系数的总位数）连接起来，这条线段只管描绘了绩效考核系数随年份的变化走势。可以认为，绩效考核系数跟年份之间是一种高度波动关系，从2000年开始到2010年，被观测的客户经理多的绩效考核系数先下降又上升，再下降又上升，又下降。
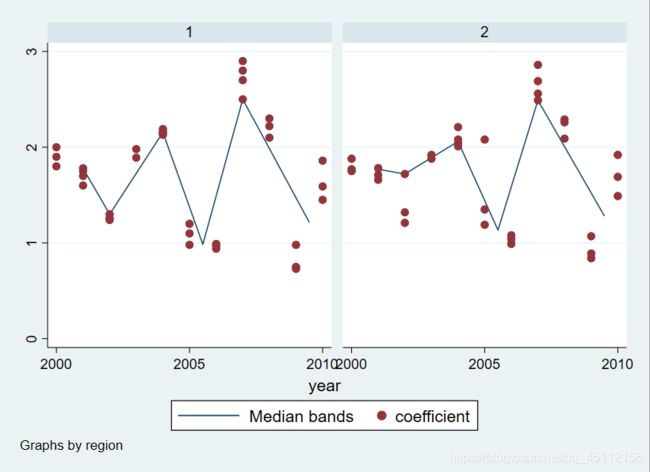
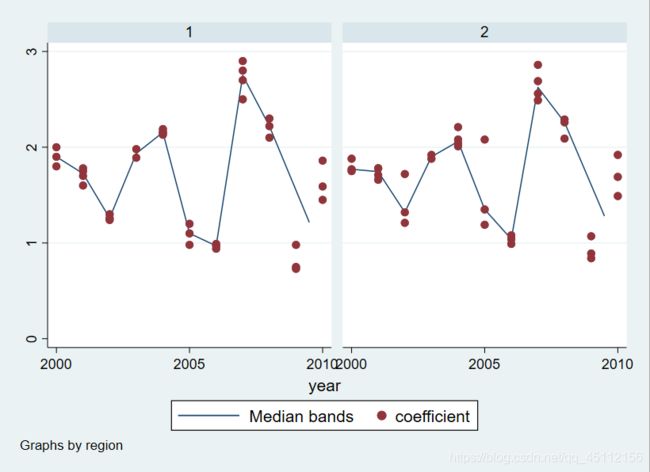
graph twoway mband coefficient year || scatter coefficient year||,by(region) #本命令的含义是以事业部为分类对数据进行非参数回归，并且绘制年份与绩效考核系数之间的散点图
从图中可以看出北方事业部和南方事业部的绩效考核系数的整体走势是很相近的，但是南方事业部的波动要相对平滑一些。
lowess coefficient year if region == 1 #本命令是对数据进行修匀，这是非参数回归的另外一种重要形式
从图中我们可以看出，在修匀的情况下绩效考核系数一直绕着一条值约为1.6的中轴线上下波动，可以初步判定该公司的客户经理的绩效水平是比较高的 。
graph twoway lowess coefficient year if region==1 || scatter coefficient year #旨在把修匀命令融合到非参数回归中
该结果与上图是一致的。
案例延伸
延伸1：设定散点图被分成垂直等宽波段的数量
graph twoway mband coefficient year ,bands(10) || scatter coefficient year 
从上图可以看出，相对于系统默认设定，散点图得到了更加细致的划分，绩效考核系数走势也更加清晰明朗。
graph twoway mband coefficient year ,bands(10) || scatter coefficient year || , by(region)
#以事业部为分类对数据进行非参数回归，并把散点图分成10段垂直等宽的波段
延伸2：设定修匀的波段宽度
例如：要设定对没一点进行修匀的样本比例为0.4
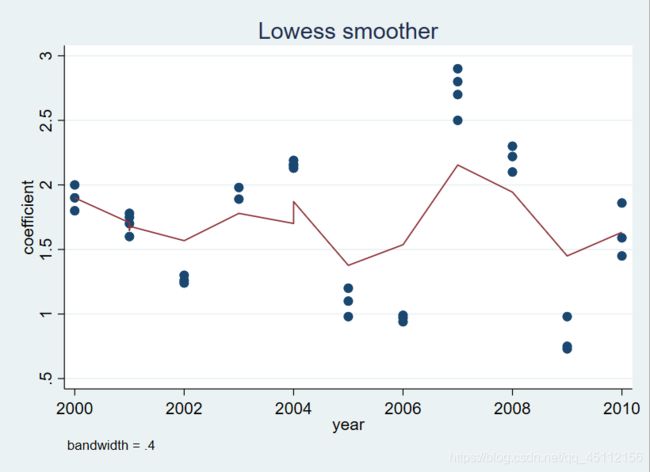
lowess coefficient year if region == 1,bwidth(0.4)
从上图可以看出，数据的波动性得到了增强，修匀程度得到了进一步的降低。系统默认的修匀样本比例是0.8，波段宽度也就是修匀样本比例越接近于1，数据修匀的程度越低。
12.2转换变量回归分析
转换变量回归分析是解决变量间非线性关系的重要方法之一，基本思想是对一个或者更多的变量进行恰当行是的非线性转化，然后将转换好的变量纳入到线性回归分析模型中进行分析。由此可见转换变量回归分析在本质上仍属于线性回归分析的范畴。但它的确是解决描述变量间非线性关系的较好方法。
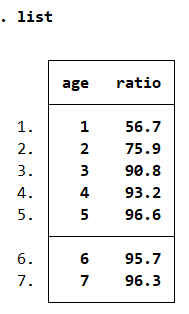
数据（案例12.2）研究发现，锡克氏实验阴性率随着而同年年龄的增长有所升高。山东某1-7岁儿童锡克氏实验阴性率如下图所示，试用转换变量回归分析方法拟合曲线。变量为年龄age、阴性率/%ratio。
sum age ratio ,detail #对变量进行描述性统计
twoway line ratio age #通过绘图，从整体上对数据有一个清晰直观的把握
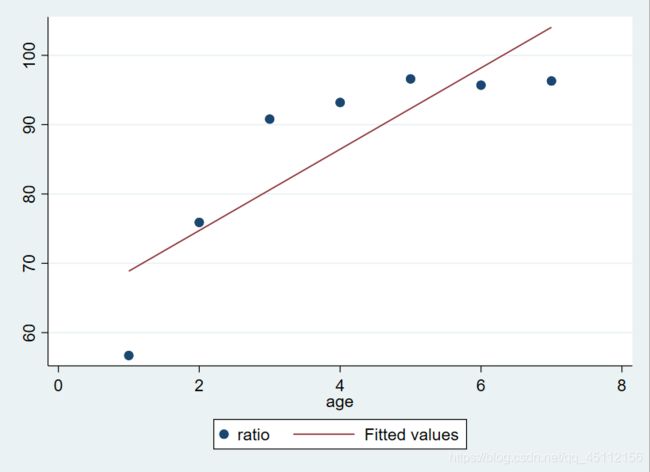
graph twoway scatter ratio age || lfit ratio age #通过绘图，从整体上对数据有一个清晰直观的把握
我们可以看到，阴性率随着年龄的上升而上升，但是上升的速度越来越慢，因此初步构想的模型包括线性、对数、二次、三次等。
reg ratio age #对两个便令进行回归分析
gen lnage=log(age) #对年龄变量进行自然对数变换。
reg ratio lnage #对两个变量进行回归分析
gen age2 = age^2
reg ratio age2 age
gen age3 = age^3
reg ratio age3 age2 age 当大家运行完之后，大家看得是谁和谁得关系？当然是ratio和age 得了，我们只不过是为了提高模型得解释程度和显著性。大家可能会想变量变化之后不是原来变量了这···想多了，我们还是看自己原来得目的就好。结果不过多赘述。
12.3非线性回归
上节讲述的转换变量回归分析从本质上讲仍属于一种线性回归分析方法，而师级问题往往会更加复杂，使用转换变量回归分析方法便无从做出准确的分析，这时候就需要用到Stata的非线性回归。非线性回归分析是一种功能更强大的处理非线性问题的方法，可以使用户自定义任意形式的函数，从而更加准确的描述变量之间的关系。
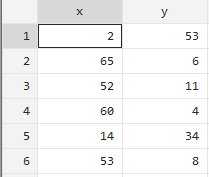
数据（案例12.3）是某著名总裁培训班想要建立一个回归模型，对参与培训的企业高管毕业后的长期表现情况进行预测。自变量是高管培训天数（X）因变量是高管毕业后的长期表现指数（y），指数越大表现越好。
sum y x ,detail #对两个变量进行描述性统计
twoway line y x #绘制两个变量的线型图，从整体上对数据有一个清晰直观的把握。
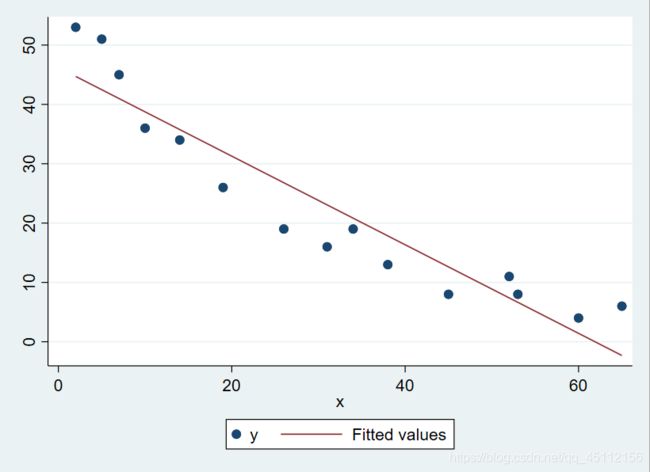
graph twoway scatter y x || lift y x #绘制线型图，从数据上有一个把握
可以看出长期表现指数随着培训天数的上升而下降
reg y x #进行最小二乘回归分析，探索变量之间的关系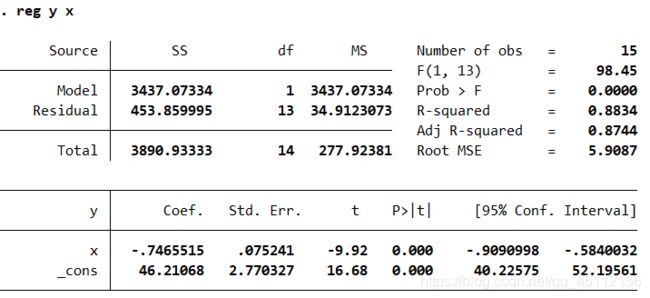
从上图我们可以看出线性模型的整体显著性和系数显著性尚可，但是模型的整体解释能力又较大的提升空间
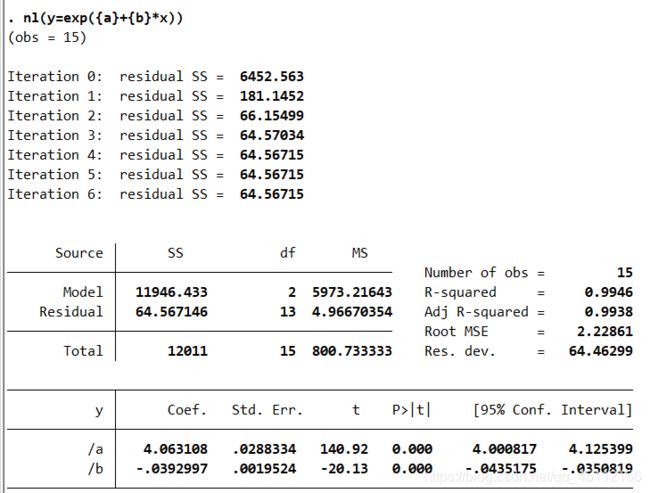
nl(y=exp({(a)+(b)*x})) #构建非线性模型 nl(y=exp({(a)+(b)*x}))
y=EXP(4.063108-0.0392997*x)
我们可以看出非线性回归模型在保持整体显著性和系数显著性比线性模型很高的基础上实现了模型的整体解释能力的较大提升。
vce #本命令旨在估计系数a和b的方差-协方差矩阵
predict yhat #本名旨在获得因变量的拟合值
predict e ,resid #获得残差案例延伸
延伸1：设定非线性回归模型中被估计参数的初始值
nl (y = exp({a}+{b}*x)),initial(a 4 b -0.04)
从上图可以看出由于 初始参数值的设定减少了迭代次数，提高了系统运行效率，结果与前面是一致的。
延伸2：采用文件的标准差进行非线性回归估计
nl (y = exp({a}+{b}*x)),robust延伸3：采用系统默认快捷函数进行非线性回归
| 非线性函数命令缩写 | 非线性函数形式 |
| exp2 | y = b1*b2^x |
| exp3 | y = b0+b1*b2^x |
| exp2a | y = b1*(1-b2^x) |
| log3 | y = b1/(1+exp(-b2*(x-b3))) |
| log4 | y = b0+b1/(1+exp(-b2*(x-b3))) |
| gom3 | y=b1*exp(-exp(-b2*(x-b3))) |
| gom4 | y=b0+b1*exp(-exp(-b2*(x-b3))) |
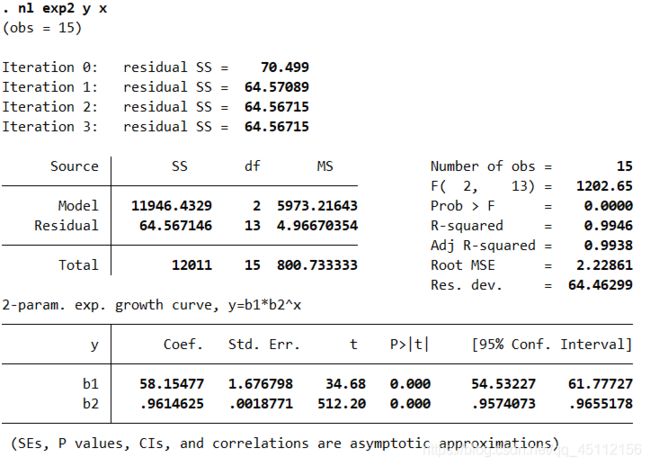
例如：在本例中我们设定非线性模型回归形式为：y = b1*b2^x
nl exp2 y x回归方程：y = 58.15477*0.9614625^x
