语义分割——FCN

写在前面，本文的实例运行目前只有FCN8；FCN-8s均优于FCN-16s，FCN-32s。

FCN浅显的介绍

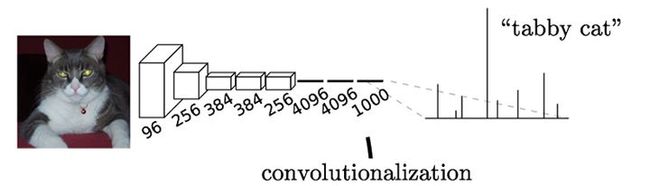
要介绍FCN（Fully Convolutional Networks），首先从CNN角度出发介绍二者的不同。通常CNN网络在卷积层之后会接上若干个全连接层。将卷积层产生的feature map(特征图)映射成一个固定长度的特征向量。以AlexNet为例，最后期望得到整个输入图像的一个概率值，比如AlexNet的ImageNET模型输出一个1000维的向量表示输入图像属于每一类的概率。如下图所示：

而FCN对图像进行像素级的分类，对每个像素都产生一个预测；解决了语义级别的图像分割(semantic segmentation)。与CNN最后的全连接层+softmax，使用全连接层得到固定长度的特征向量进行分类不同；FCN可以接受任意尺寸的Input image,采用反卷积层对最后一个卷积层的feature map进行上采样，将他恢复到原来的尺寸，从而可以对每个像素都产生一个预测，同时保留了原始输入图像中的空间信息，最后在上采样的特征图上进行逐像素分类。

最后逐个像素计算softmax分类的损失，相当于每一个像素对应一个训练样本。如下图所示：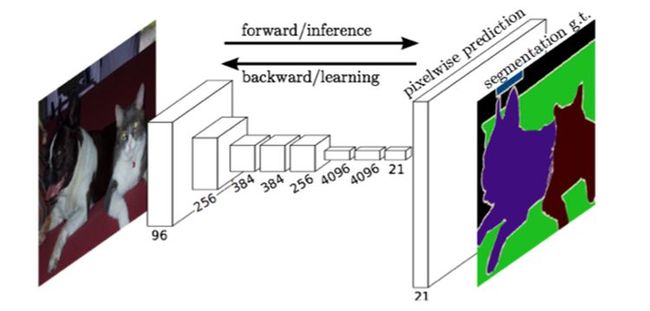

或者说，FCN与CNN的区别在于，FCN将CNN最后的全连接层换成卷积层，输出一张已经Labe好的图片。

关于全连接层->全卷积层

（理解参考知乎）全连接层和卷积层之间的区别在于卷积层中的神经元只与输入数据中的一个局部区域连接，并且在卷积核中的神经元共享参数；但是无论是前者还是后者，神经元都是计算点积，故而二者相互转化是可能的。

• 对于任一个卷积层，都存在一个能实现和它一样的前向传播函数的全连接层。权重矩阵是一个巨大的矩阵，除了某些特定块，其余部分都是零。而在其中大部分块中，元素都是相等的。
• 相反，任何全连接层都可以被转化为卷积层。比如，一个 K=4096 的全连接层，输入数据体的尺寸是 7∗7∗512，这个全连接层可以被等效地看做一个 F=7,P=0,S=1,K=4096 的卷积层。换句话说，就是将滤波器的尺寸设置为和输入数据体的尺寸一致了。因为只有一个单独的深度列覆盖并滑过输入数据体，所以输出将变成 1∗1∗4096，这个结果就和使用初始的那个全连接层一样了。（F:滤波器尺寸；P：pad属性值；S：滤波器每次移动的步长；K：滤波器的个数）

全连接层转化为卷积层：

如果我们想让224×224尺寸的浮窗，以步长为32在384×384的图片上滑动，把每个经停的位置都带入卷积网络，最后得到6×6个位置的类别得分。上述的把全连接层转换成卷积层的做法会更简便。如果224×224的输入图片经过卷积层和下采样层之后得到了[7x7x512]的数组，那么，384×384的大图片直接经过同样的卷积层和下采样层之后会得到[12x12x512]的数组。然后再经过上面由3个全连接层转化得到的3个卷积层，最终得到[6x6x1000]的输出((12 – 7)/1 + 1 = 6)。这个结果正是浮窗在原图经停的6×6个位置的得分.

• 面对384×384的图像，让（含全连接层）的初始卷积神经网络以32像素的步长独立对图像中的224×224块进行多次评价，其效果和使用把全连接层变换为卷积层后的卷积神经网络进行一次前向传播是一样的。
• Evaluating the original ConvNet (with FC layers) independently across 224x224 crops of the 384x384 image in strides of 32 pixels gives an identical result to forwarding the converted ConvNet one time.

而FCN对应CNN网络，把最后三层全连接转换成三层卷积层。在传统的CNN结构中，前5层是卷积层，第6层和第7层分别是一个长度为4096的一维向量，第8层是长度为1000的一维向量，分别对应1000个不同类别的概率。FCN将这3层表示为卷积层，卷积核的大小 (通道数，宽，高) 分别为 (4096,1,1)、(4096,1,1)、(1000,1,1)。看上去数字上并没有什么差别，但是卷积跟全连接是不一样的概念和计算过程，使用的是之前CNN已经训练好的权值和偏置，但是不一样的在于权值和偏置是有自己的范围，属于自己的一个卷积核。因此FCN网络中所有的层都是卷积层，故称为全卷积网络。

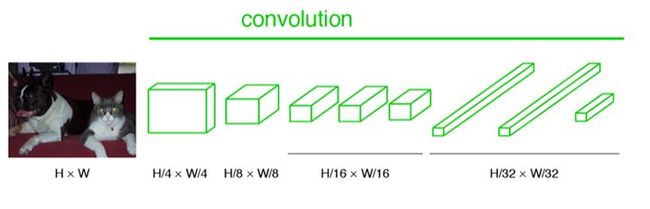经过多次卷积和pooling以后，得到的图像越来越小，分辨率越来越低。其中图像到 H/32∗W/32 的时候图片是最小的一层时，所产生图叫做heatmap热图，热图就是我们最重要的高维特诊图，得到高维特征的heatmap之后就是最重要的一步也是最后的一步对原图像进行upsampling，把图像进行放大、放大、放大，到原图像的大小。最后的输出是1000张heatmap经过upsampling变为原图大小的图片，为了对每个像素进行分类预测label成最后已经进行语义分割的图像，这里有一个小trick，就是逐个像素地求其在1000张图像该像素位置的最大数值描述（概率）作为该像素的分类。因此产生了一张已经分类好的图片，如下图右侧有狗狗和猫猫的图。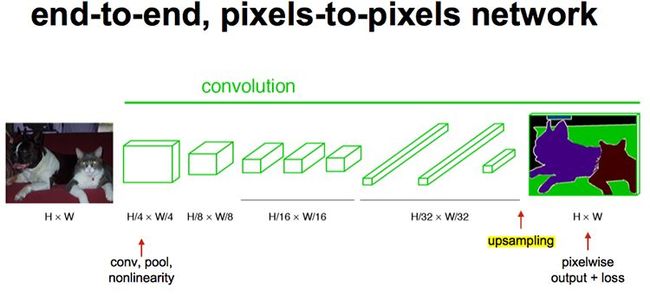

为什么区分FCN8,FCN16,FCN32呢？

因为将图片进行5次pool计算，将图片downsampling到原图的1/32时得到的heatmap恢复到原图的尺寸会丢到很多像素信息从而丧失细节信息，因此使用的trick，将heatmap与前面拥有较多细节信息的层相加，然后进行upsampling。论文中展示如下图：

在上图中，image是原图像，conv1-conv5为卷积操作，pool1-pool5为池化操作，pool操作使得输出图片变为输入图片的1/2。 conv6-conv7是最后的卷积层，最右边一列是upsample后的end-to-end的结果。nx 这代表了up多少倍可以恢复到原图的尺寸；

先看FCN-32S,因为经过conv6-7后，输出的尺寸依然是原图的1/32，因此经过32x的upsampled prediction，图片变回原尺寸大小。这里的具体操作是增加一个卷积层，在源码中卷积核的尺寸大小为64；

把一二行连起来看，把pool4的特征图拿出来，把conv7的尺寸扩大两倍至原图的1/16（具体操作是增加一个卷积层，卷积后特征图大小为con7的2倍）;将二者fuse（实际就是相加）,通过反卷积扩大16倍得到原图一样的尺寸；FCN中的upsample实际是通过增加卷积层，通过bp反馈的训练方法训练卷积层达到end to end，此时卷积层的作用可以看作Pool的逆过程；

最后看第1行与第3行，conv7经过一次4x upsample，即使用一个卷积层，特征图输出大小为conv7的4倍，所以4x conv7的大小为4x4，然后pool4需要一次2x upsample，变成2x pool4，大小也为4x4，最后吧4x conv7，2x pool4与pool3进行fuse，得到求和后的特征图，最后增加一个卷积层，使得输出图片大小为pool3的8倍，也就是8x upsampled prediction的过程，最后也得到一个end to end的图像。同时FCN-8s均优于FCN-16s，FCN-32s。

实验部分

本博客参考的代码链接如下：

https://github.com/bat67/pytorch-FCN-easiest-demo/

关于数据集的解释，这是该GitHub作者提供的一个不到80M的数据，是一些随机背景上一些包的照片。

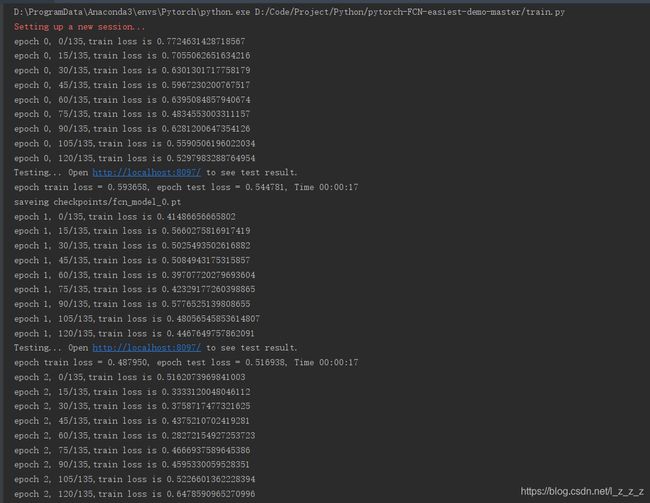
运行结果：（一共运行了100个epoch）

 

  

上图为使用Visdom可视化，运行了100个Epoch后的结果。

结果可视化（VISDOM）：

关于结果可视化遇到的一些困难的解决办法：

(5条消息) pytorch visdom安装启动问题_zj-CSDN博客