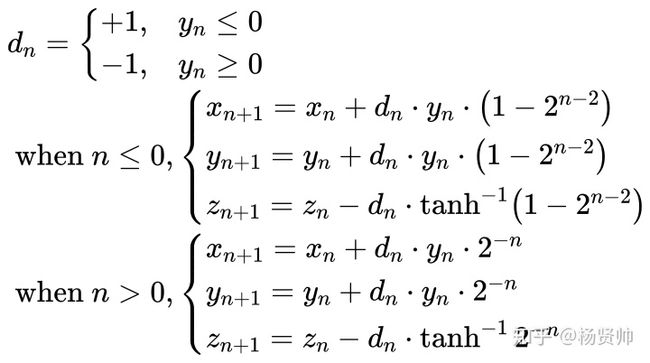plsql如何实现求对数指数_Chisel实践——利用CORDIC算法计算对数函数
Chisel实践——利用CORDIC算法计算对数函数
一、介绍
在本专栏之前的文章中:
用Chisel快速搭建FFT流水线电路
Chisel实践 —— 短时傅里叶变换模块的实现与测试
已经介绍到了如何使用Chisel开发FFT运算模块和STFT模块,此篇文章将详细介绍如何使用Chisel进行对数运算模块的开发。
如何使用硬件语言实现对数运算,在兼顾精度的同时又要节约面积,这是极其困难的一件事。目前工业界比较流行的方法有查表法、泰勒展开以及线性近似法等,这些算法各有优缺点:
· 查表法:实现简单,但是所需要的存储单元随着精度的增加或输入值范围的增大而成指数增加,在计算高精度,多位宽的数据时,查表法是显然不合适的;
· 泰勒公式展开法:需要乘法器,面积大且不易实现;
· 线性近似法:精度有限,且需要误差校正电路,仍要耗费大量的面积,实现上较为困难。
本篇文章将介绍采用CORDIC(Coordinate Rotation Digital Computer)算法 , 即标旋转数字计算方法进行对数运算,该算法主要通过基本的加和移位运算代替乘法运算, 用矢量的旋转和定向间接计算三角函数、双曲线、指数、对数等函数。采用CORDIC算法来实现这类函数时,无需使用乘法器,它只需要一个最小的查找表(LUT),利用简单的移位和相加运算,即可产生高精度的结果,尤其适合FPGA的实现。 本文将简要阐述CORDIC算法,以及如何使用Chisel语言实现基于CORDIC算法的对数函数实现。
二、算法说明
CORDIC算法是基于移位加法和矢量旋转技术进行计算的。它主要有旋转模式(Rotation Mode)和向量模式(Vectoring Mode),两种模式又可以应用在圆坐标系、线性坐标系以及双曲坐标系。两种模式分别应用在三个坐标系,进行迭代运算,可以分别演算出8种运算。主要如下表总结(主要是各个模式应用在不同坐标系可以实现的函数说明)。
2.1 旋转模式
如图所示,假设在一个圆周系统中,若是想求得30°的cos值与sin值,那需要得到30°角在单位圆上交点的x轴坐标与y轴坐标。
首先,赋予初值x0 = 1,y0 = 0,z0 = θ(此个例子中θ为30,zi执行加或者减操作,使得z的最终值为0 ,该条件由di决定)
为了得到30°角在单位园上的x轴坐标与y轴坐标,我们先将初始线逆时针旋转45度,得到相应的x1、y1、z1值。其次比较得出45°角比30°角大,因此要进行第二次旋转,进行顺时针旋转26.6°角,得到x2、y2、z2值。又发现新得到的角度比30°角小,再次旋转。就依靠这种模式进行N次迭代,迭代次数越大,那么实现的精度就会越高,以此类推。z的迭代过程是将z收敛于零的过程,也正是将θ分解为一系列θi的过程, 故zi可认为是第i次旋转剩余的角度。
此过程具体的数学推导,有兴趣的读者可以参考这篇文章。
2.2 向量模式
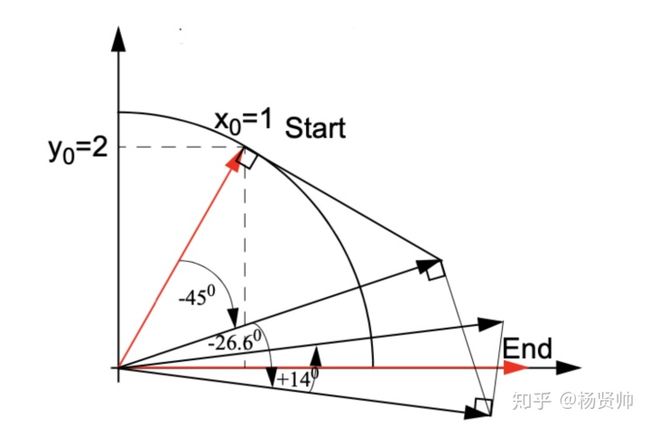
与旋转模式相比,向量模式下的目的是使y趋向于 0。 为了达到这一目标, 每次迭代通过y值的正负性确定旋转方向, 最终使初始向量旋转至 x轴的正半轴, 这一过程也使得每次微旋转的旋转角度累加和存储在变量 z 中。
如图当设置初始值y0 = 2 ,x0 = 1的时候,经过n(n–>∞)次旋转,开始的点靠近x轴。因此,当迭代结束之后,P将近似接近x轴的正半轴,此时P点纵坐标yn = 0,在这个过程中可知旋转了θ,即zn = z0 +θ = z0+arctan(y0/x0) (z0为初始化角度)。
2.3 双曲系统
与圆周系统和线性系统有所不同, 双曲系统的迭代较为复杂。但是利用双曲系统可求取一系列超越函数。例如 在旋转模式下, 可求取双曲正弦函数和双曲余弦函数, 进而可求取 e 指 数,在向量模式下, CORDIC 算法可实现反双曲正切函数的计算。当我们要实现对数函数求解时,可以从如下公式出发:
将求解ln的值转化为求解arctanh的值。在双曲模式下的算法迭代涉及到发散收敛问题,且从N为4开始,每当3k+1的项需要重复迭代,即1,2,3,4,4,5,6,7.....13,13.....。与此同时仅进行正数迭代,那么当输入值大于9的时候就会出现严重发散的现象,这也不是我们所期望的。因此需要添加负数次的迭代,扩大定义域。在此论文中有详细说明。
三、算法过程:
3.1 逻辑说明
· 取x0 = r + 1, y0 = r-1, z0 = 0,其中r为我们想求得的值。当y经过多次迭代逼近0的时候,zn的输出值即为对数函数值的一半。本次研究取迭代次数为16次,n=-5为起始迭代数,事先通过计算求解出相应的arctanh值,作为常量供迭代方程加减。需要注意的地方是,如果输入的r值太小,可能会在迭代过程中因为移位操作导致值的丢失,建议将x值与y值同时放大, 结果并不会发生改变,但可以使得迭代更多次,保证精度。当然预先做个数值范围判定移位更佳,为了避免精度损失,本次实验研究将数值放大
· 为了抑制迭代过程发散的情况, 我们选取负数次处开始迭代,则有如下迭代公式:
注意事项:使用Verilog编写此份算法,若是定义signed要注意算术移位的问题,建议使用拼接截位操作。
3.2代码实现
import chisel3._
import chisel3.experimental._
class Mylog extends Module {
val io = IO(new Bundle {
val in = Input(SInt(32.W))
val out = Output(SInt(32.W))
})在上述代码中,自定义类Mylog继承自Chisel的Bundle类,输入、输出采用32位的符号数。若是读者想要进行更高精度的迭代计算,需要增加位宽以及迭代次数。但是会极大的增加电路的面积,因此视实际情况进行取舍。
val x0 = io.in + 65536.S(32.W)
val y0 = io.in - 65536.S(32.W)
val z0 = 0.S(32.W)
val taps_x = Seq(x0) ++ Seq.fill(16)(RegInit(0.S(32.W)))
val taps_y = Seq(y0) ++ Seq.fill(16)(RegInit(0.S(32.W)))
val taps_z = Seq(z0) ++ Seq.fill(16)(RegInit(0.S(32.W)))
io.out := taps_z(16)我们先将x0、y0 、z0进行初始化,用于后面的迭代计算,通过Seq函数搭建各个位置的节点,这是类似于搭建移位寄存器,但是各个节点间的连接关系我们仍然可以自行定义,这样有利于不同计算间的输入定义,是编写Chisel代码很有效的一种技巧。最后将输出连接z16节点的输出,得到解值。
val taps_xy = taps_x.zip(taps_y).zip(taps_z)
taps_xy.zip(taps_xy.tail).zipWithIndex.foreach { case((((x0,y0),z0),((x1,y1),z1)),index) =>
when (y0(31) === 1.U) {
if (index <= 5) {
x1 := x0 + y0 - (y0 >> (7 - index))
y1 := y0 + x0 - (x0 >> (7 - index))
z1 := z0 - rot(index).S
}
else if (index <= 9) {
x1 := x0 + (y0 >> (index - 5))
y1 := y0 + (x0 >> (index - 5))
z1 := z0 - rot(index).S
}
else {
x1 := x0 + (y0 >> (index - 6))
y1 := y0 + (x0 >> (index - 6))
z1 := z0 - rot(index).S
}
}
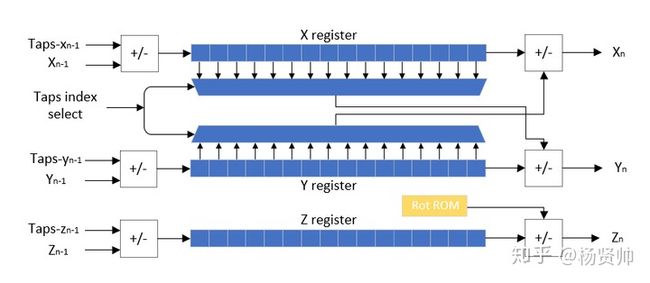
.......笔者先将前15位节点与后15位节点捆绑在一个元组中,类似于(x0,y0,x1),这样可以很方便的将x1的输入与x0,y0联系起来。然后再包裹一个zipWithIndex函数用于标记元组位置,可以方便迭代位移操作。最后使用foreach函数进行移位连接赋值操作,即可快速搭建迭代电路逻辑。下图为迭代设计实现结构图,描述电路工作状态。
四、模块测试与说明
4.1 基于Chisel实现16次迭代32位输入CORDIC模块测试
首先运行测试脚本,使用scansion对生成波形进行测试。将输入测试值放大
输出端口得到的数据是经过放大处理后的值,将其输出值除以
图示为部分波形截图,io_out输出为ln(3)、ln(4)...ln(16)的解值。
下图为整体测试运行波形图,将输出波形与精确值进行对比分析,误差在0.5%上下浮动。
4.2 Berkeley dsptools模块测试
在此连接提供了berkeley研发的dsptools库。 dsptools库是一个可以和任何Chisel工程混合使用的库。该库提供了包括流水线延迟检查,DSP设计和验证等功能,以及更多针对不同数值类型的验证平台。
要说明的是,dsptools中函数部分继承于BlackBox,通过BlackBox导入Verilog模块的端口列表给Chisel模块使用。其中,ln函数就是通过BlackBox导入,同时其调用的Verilog代码使用了scala系统函数,因此实际上该函数仅作为验证,其代码不可综合的,读者需引起注意。
在Chisel中写dsptools的测试脚本时,可以直接输入双精度浮点数,利用FixedPoint.fromDouble(value , DataWidth.W, BinaryPoint.BP) 将其转为定点数进行输入。输出可以利用波形显示工具转为 float 64 类型观察测试。
下图为berkeley dsptools库中调取ln函数测试波形图,截取ln(3)至ln(16)输入输出波形图,用于对比分析。
CORDIC算法实现的ln(6)的输出为118260,将其除以
4.3 与Vivado CORDIC IP对比测试
Vivado提供的CORDIC IP 6.0,同样可以完成三角函数、双曲线、指数、对数等函数的计算。
Vivado CORDIC IP核有两种架构配置:并行架构(Parallel),具有单周期多数据的吞吐量但是耗费较大面积。字串行架构(Word Serial) ,具有多周期的吞吐量但是面积消耗小。本次实验选择字串行架构,配置32位有符号定点二进制数作为输入、输出,选择16次迭代次数。
(特别要注意的是,输入X_IN以及输出Y_IN被限制在如下表格给出的范围内,超出这些范围的输入会产生不可预测的输出。 此外,|Y_IN|必须小于或者等于(4/5*X_IN),否则CORDIC算法输出会有不收敛的情况。)
X_IN以及Y_IN输入为宽度2位的定点二进制补码,PHASE_OUT输出为宽度3位定点二进制补码。举个例子:
若求ln(K),其中K = 0.625,则 K+1 = 1.625 ,K - 1 = -0.375。
X_IN = K + 1 = '01,10 1000 0000 0000 0000 0000 0000 0000 ' = 32'h6800 0000
Y_IN = K - 1 = '11,10 1000 0000 0000 0000 0000 0000 0000 ' = 32'hE800 0000 (负数已经做过补码处理)
PHASE_OUT = '111,0 1101 0110 0011 1110 0011 0110 0010 ' = 32'hED63E362另外要说明的是,若是求解超出范围的整数值,要先实现一个预处理模块,将K转换为P*2N (P ∈[0.5 , 1) ,N为偶数 ),倘若K值转换出来的等式中N为奇数,则将P值除以2使得N = N + 1,此时P∈[0.25 , 0.5) 。
举个例子: 计算ln(160),则K = 160,可以换算为0.625 * 28,即P = 0.625,N = 8,此时ln(160) = ln(0.625) + 8 * ln(2)。 此时需要:
- 预先存储ln(2) 的值
- 使用Vivado CORDIC IP核计算ln(0.625)
- 通过乘法与加法得到最终结果
4.3.1 精度对比测试
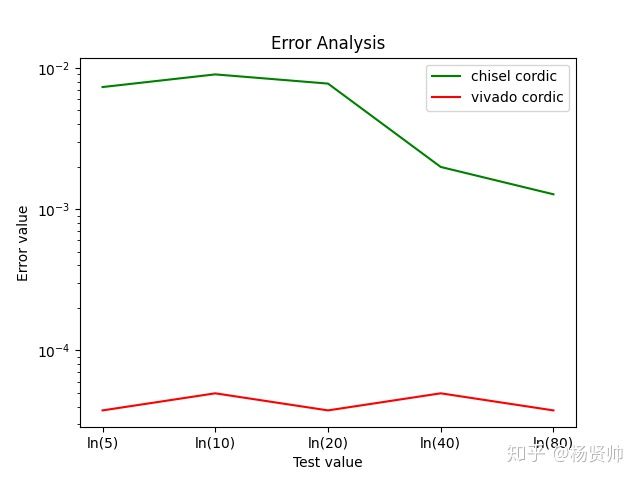
使用Vivado CORDIC IP 6.0搭建测试模块,采用16次迭代32位输入,IP核将会产生20个周期的延迟,将随机值(此处取5个随机点作为展示)与Chisel实现的16次迭代32位输入CORDIC模块比较(产生16个周期的延迟)。图中横坐标表示测试的数值,纵坐标表示不同运算结果误差绝对值。
可以发现:32位输入20周期延迟的Vivado CORDIC IP 6.0,在精确度上是远优于32位输入16周期延迟基于Chisel实现的CORDIC模块。
通过实验研究,我们发现Vivado提供的IP输入值限定最大值为1.00,原因是通过增加定点小数位(30位)来提高精度,而我们设计的Chisel CORDIC模块输入定点值格式为32位宽,16位小数,动态范围更大,但是计算精度更低。 为此我们进行代码的改进,基于Chisel实现32位输入20周期延迟的CORDIC模块,将模块的输入值范围限定为30位小数的32位定点数,重新对其误差以及资源进行了分析。注:下文出现的VIVADO IP表示30位小数的32位定点数输入,20周期延迟的CORDIC IP 6.0模块; Chisel-16表示输入为16位小数的32位定点数,16周期延迟Chisel实现的CORDIC模块; Chisel-20表示输入为30位小数的32位定点数,20周期延迟Chisel实现的CORDIC模块。
我们一共测试了92组数据(数据由Python随机函数产生),在同样的延迟周期和同样的定点范围下得到和Vivado IP的误差对比(下图表示VIVADOC IP 以及Chisel-20 输出值与实际的误差):
下述为各个模块的均方误差值
MSE of VIVADO IP:4.177e-07
MSE of chisel-16:4.004e-05
MSE of chisel-20:2.872e-08此时的Chisel-20模块误差已经和Vivado CORDIC IP的误差为一个量级。从均方误差方面分析,Chisel-20的精确度是最具有优势的。
4.3.2 资源对比测试
通过Vivado进行FPGA评估,我们选定FPGA元件为v7xc7vx485tffg1761-2,工作频率为200MHz,通过综合工具和实现工具,对三种不同IP进行资源评估和功耗分析。
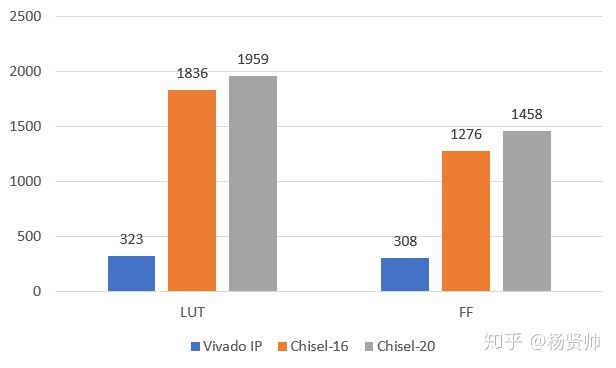
三种方式的资源消耗关键数值对比如下所示:
对比分析得知,相对于Chisel-16、Chisel-20模块,Vivado IP的LUT、FF资源消耗少,LUTRAM、IO资源占用高。
分析Chisel-16和Chisel-20模块可知,随着Chisel-20模块精度提升,其LUT、FF资源消耗也相应增加。
总的来说基于Chisel设计的CORDIC模块需要更多LUT和FIFO资源,更少的IO资源。
4.3.3 总结分析
通过数据对比分析,在同样的延迟周期和同样的定点范围条件下,我们设计的CORDIC模块和Vivado提供的IP核区别如下:
| Chisel-16 CORDIC | Vivado CORDIC IP | Chisel-20 CORDIC | |
|---|---|---|---|
| 延迟周期 | 16 | 20 (字串行) | 20 |
| 是否需要预处理 | 否 | 是 | 否 |
| 求值范围ln(K) | K∈(0 , 32768] | K∈(0 , 1] | K∈(0 , 1] |
| 总功耗(200MHz) | 0.531W | 0.381W | 0.565W |
| 精度 | 低 | 高 | 高 |
| WNS | 2.408ns | 1.781ns | 1.191ns |
| WHS | 0.054ns | 0.145ns | 0.093ns |
| WPWS | 1.100ns | 1.100ns | 1.100ns |
总的来说三种方式设计的CORDIC模块在200MHz的工作频率下,S/H时序都满足要求,总功耗为Chisel-20 CORDIC模块最大, Vivado CORDIC IP core 与 Chisel-20 CORDIC精度相近。
4.3.4 注意事项
进行FPGA评估需要通过修改Vivado的tcl脚本fft.tcl中的参数,具体设置以及流程可以看此文档中的说明,主要修改tcl中的路径以及top文件名。同时要注意的是,引用Verilog文件中的顶层的模块时,需要添加时钟模块来驱动clock,主要代码参考如下:
wire clock;
clk_wiz_0 clk_wiz_0_inst0(
.clk_out1(clock),
.clk_in1_p(clk_in1_p),
.clk_in1_n(clk_in1_n)
);
五、结语
本文简单介绍了CORDIC算法的应用实现,通过数十行Chisel代码实现了对数函数的电路设计。同时,笔者尝试编写了一份实现相同功能的Verilog代码,发现Chisel在代码量上以及效率上是具有极大优势的,使用Chisel设计结构重复性硬件大大简化了电路的设计过程。
六、参考文献
-[1]Mopuri, S., Acharyya, A. Configurable Rotation Matrix of Hyperbolic CORDIC for Any Logarithm and Its Inverse computation.
-[2]CORDIC v6.0 Document