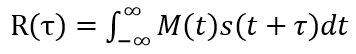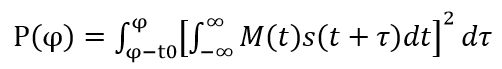目标反射回波检测算法及其FPGA实现之一:算法概述
前段时间,接触了一个声呐目标反射回波检测的项目。声呐接收机要实现的核心功能是在含有大量噪声的反射回波中,识别出发射机发出的激励信号的回波。我会分几篇文章分享这个基于FPGA的回波识别算法的开发过程和原码,欢迎大家不吝赐教。以下原创内容欢迎网友转载,但请注明出处: https://www.cnblogs.com/helesheng。本文首先简要介绍基于FPGA的互相关反射回波检测算法的主要设计思路。
声呐测距的原理非常简单,如下图所示,抹香鲸在水下发射特定的声波信号,并监听感兴趣的对象(乌贼)反射的该声波的回波。抹香鲸就可以根据回波的时间、幅度和相位的信息,“推算出”乌贼的方位、距离、速度和体表硬度等基本物理信息。
图1 声呐基本原理示意图
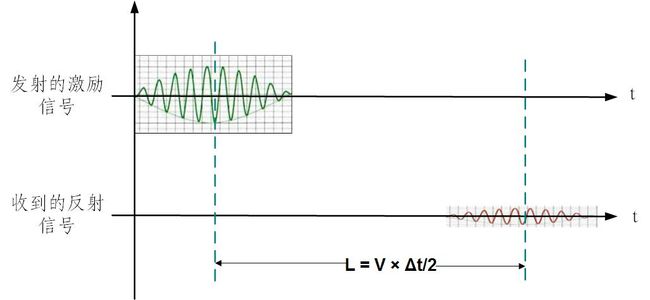
这里我们只讨论最简单的物理信息——距离。抹香鲸可以根据反射波到达的时间“计算”出和猎物之间的距离:L=V×Δt/2
图2 声呐测距示意图
由上图可知,声呐测距的问题可以被简化为:如何在接收到的信号中准确的定位出发射信号的反射回波。造成反射信号定位困难的原因有二:反射信号经过目标反射和长距离传播后信号强度大大降低;大量的噪声进一步降低了接收信号的信噪比。
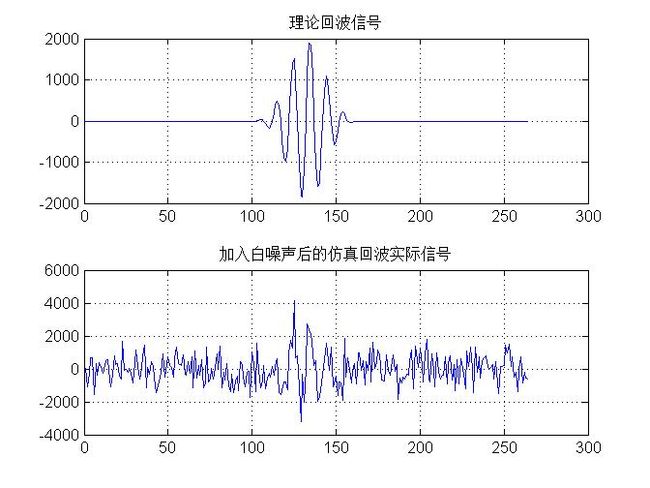
下图上方是对一段长度为64个采样点的正弦信号(约6个周期)加blackman窗后得到的理想回波信号。下图下方则是用matlab产生的仿真回波信号,其中加入了标准差为800白噪声。可以看出,想不经过任何算法就得到反射回波的位置不是一件容易的事。
图3 理论回波信号和加入了噪声后的仿真回波信号
一种最直接的思路是对信号求短时傅里叶变换(short-time FFT)。在Matlab中仿真这一过程的MATLAB代码如下。
%%这个脚本用于验证短时傅里叶变换检测回波的算法
i=1:60;
s=2000*sin(2*pi*i*6/60);%加了blackman窗的信号模板
s=[0,0,s,0,0];
s=s.*(blackman(64))';
sl=[zeros(1,100),s,zeros(1,100)];%两边扩展后的信号
figure;
subplot(2,1,1);
plot(sl);grid;
title('理论回波信号')
n=randn(1,264)*800;%方差为800的噪声信号
slp=sl+n;%加入噪声后的扩展信号
subplot(2,1,2);
plot(slp);grid;
title('加入白噪声后的仿真回波实际信号')
[S,F,T,P]=spectrogram(slp,64,63,64,50E3);%slp为信号,64为加窗的长度,60为每次傅里叶变换交叠部分的长度,64为傅里叶变换的长度,50E3是采样率。
figure;
surf(abs(S));
xlabel('时间')
ylabel('频率')
zlabel('信号强度')
title('短时傅里叶变换得到的时频图')
得到仿真回波信号的时频图如下所示。从图中可以发现短时短时傅里叶算法能够成功的检出回波出现的时间。 
图4 短时傅里叶变换得到的时频图
但采用短时傅里叶变换搜索反射回波的办法有以下缺点:
1、FFT算法的乘加计算的计算量为N*Log(N),例如,当窗口长度为64时,进行的乘加运算次数为64*6=384次MAC(乘加)运算。为了获得最够高的时域分辨率和目标定位精度,需要足够高的短时傅里叶窗口交叠率(overlap rate)。例如,为了获得固定采样率下的最高定位精度,每次采样后都应该进行一次FFT,每个A/D采样间隔要执行的计算量是384次MAC。
2、短时傅里叶变换需要对信号加窗截断为较短的长度分别进行FFT,以提高结果在时域的分辨率,而加窗会在截断边界处产生能量泄露效应。而这一点在上图中就有所体现,在时频图的边界处产生较大的干扰,影响算法对回波位置的判断。
3、短时傅里叶变换只在激励信号为正/余弦信号时才有效。如果激励信号在频域不是一根唯一的谱线(也就是非正/余弦信号),则反射回波中也会含有其他频率分量,对其实施FFT就很难判断哪些是激励哪些是噪声了。
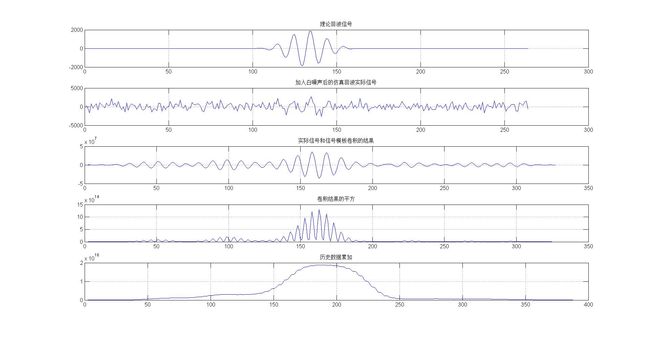
一种更优的算法使通过计算激励信号M(t)和反射回波s(t)的互相关:
来搜索反射回波在时间轴上的位置。其物理解释是:在回波信号中搜索和激励信号M(t)“最相似”的地方,从而定位哪里最像回波信号。下图是对没有添加噪声的理论回波信号相关的结果。
图5 理论回波信号和激励的互相关
显然,由于激励信号具有一定的周期性,导致互相关结果具有更加复杂的周期性结构。如果直接采用式(1)的结果来计算回波位置是不明智的,需要进一步通过积分环节来降低结果中的高频周期拨动。当然,由于互相关结果R(τ)的直流分量为0,直接对其积分也不行。可以先对其求平方,以产生与R(τ)的功率成正比,且只有正值的信号,才能用于积分计算。我设计了如下所示的目标函数来表征回波信号与激励信号的相似程度。
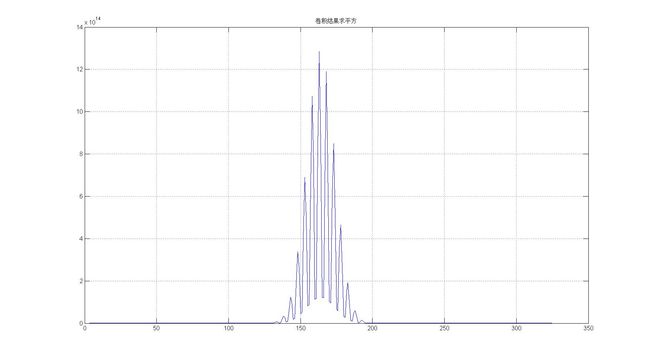
其中t0是最后一步积分求和窗口的长度,如果也取激励信号的长度,即64,则得到如下图所示的理想信号仿真结果。
图6 对互相关结果求平方的仿真
图7 对平方结果截断积分的结果
采用和上述短时傅里叶变换同样严格的加性噪声参数验证这一算法的Matlab仿真代码如下所示。
%这个脚本用于验证回波卷积算法
i=1:60;
s=2000*sin(2*pi*i*6/60);%加了blackman窗的信号模板
s=[0,0,s,0,0];
s=s.*(blackman(64))';
plot(s);grid;
title('5K信号的64个点@50KSPS')
sl=[zeros(1,100),s,zeros(1,100)];%两边扩展后的信号
figure;
subplot(5,1,1);
plot(sl);grid;
title('理论回波信号')
n=randn(1,264)*800;%方差为800的噪声信号
slp=sl+n;%加入噪声后的扩展信号
subplot(5,1,2);
plot(slp);grid;
title('加入白噪声后的仿真回波实际信号')
tp=conv(slp,s);%加入噪声后的仿真实际信号和模板卷积(由于激励信号左右对称,这里采用卷积函数conv()计算互相关)
subplot(5,1,3);
plot(tp);grid;
title('实际信号和信号模板卷积的结果')
tp1=tp.^2;%计算卷积结果的平方(能量)
subplot(5,1,4);
plot(tp1);grid;
title('卷积结果的平方')
w=ones(1,64);%矩形窗,用于通过卷积对历史数据求和
tp2=conv(w,tp1);%历史数据累加
subplot(5,1,5);
plot(tp2);grid;
title('历史数据累加')
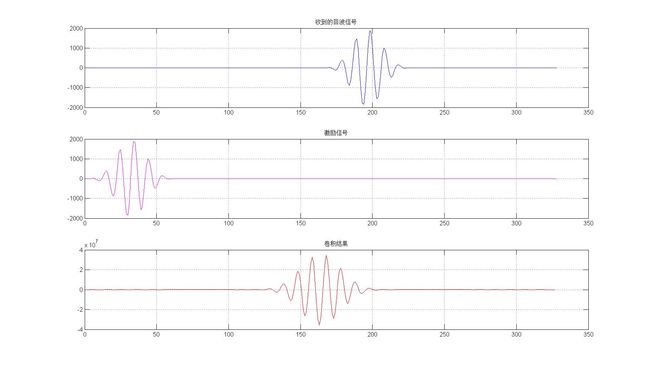
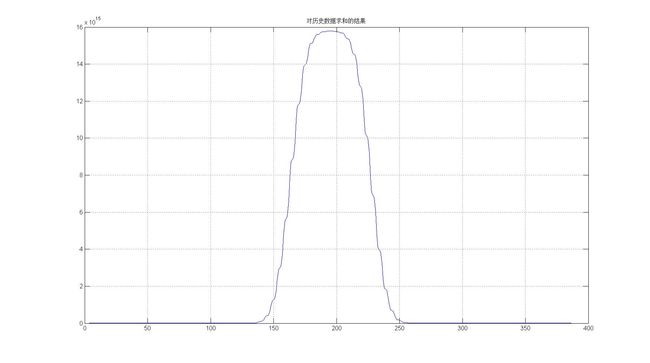
其运行结果如下图所示。
图8 对加入噪声的回波信号采用互相关算法的仿真结果
可以看出最后一行的积分结果具有相当高的信噪比,能够容易的分辨出加入噪声(方差也是800)的回波信号中回波的位置。
另外,这种算法非常好的解决了短时傅里叶变换中出现的问题:
1、相关算法的乘加计算量为N,大大小于FFT的计算量N*log(N),当激励信号长度为64个采样点时,一个采样周期中的计算量仅为64次MAC。当激励信号为左右对称的信号时,计算量可以进一步减少为N/2次乘加运算。
2、对激励加窗函数后在计算相关可以有效的避免加窗带来的泄露效应,从上图的仿真结果中可以看出(2)式积分结果两端不存在干扰。
3、可对任何形式的激励信号(如方波或锯齿波)实时相关计算,其频谱中即使存在多条谱线或连续谱也不会影响(2)式积分结果。
细心的读者会发现所谓“短时傅里叶方法”和这里提出的“互相关搜索法”具有相通之处,用通俗的语言解释:
傅里叶变换的实质就是让信号和不同频率的正弦信号相关,以计算信号和它们的“相似度”,从而得到信号在不同频率下的“功率密度”,并进一步得到频谱的。而我们直接采用互相关法的优势就在于,不在需要计算奈奎斯特频率以内其他频率正弦信号和信号的相关了。当然,由于我们搜索的就是回波中和激励信号频率相同的信号所在的位置,这种“互相关搜索法”自然能够省去“短时傅里叶方法”中大部分的计算量。
关于上述算法在FPGA中的实际实现,请关注后续博文“目标反射回波检测算法及其FPGA实现之二:互相关/卷积/FIR电路的实现”。
关于A/D和D/A转换即实验平台搭建的过程,请参看本系列的上一篇博文“目标反射回波检测算法及其FPGA实现(准备篇) —— 用Verilog-HDL状态机控制硬件接口” 。