非常适合新手入门系列-神经网络part1

这个是“非常适合新手入门系列”，这个系列专门写给大学内部分困难的课程的基础入门，帮助新手大学生解决入门时被数学公式，晦涩原理等阻挡的问题。大部分内容不涉及非常底层的原理，只是把最浅显的内容呈现出来。

想要入门最基础的神经网络之前，不能在最开始搬上来“梯度下降”，“目标损失函数”，“交叉损失函数”，“sigmoid函数”等公式，必须掌握一点基础知识：单变量线性回归，多变量线性回归，逻辑回归等。在讲解的时候我会逐渐将神经网络的相关概念展现出来。相信看完这篇文章，你在脑海中会形成神经网络的雏形。

• 现在抛出来一个问题，想要预测一个地方的房价，怎么预测？

我们从最简单的开始，假如房价只和面积有关，那我们怎么解决呢？

现在收集到三个样本：50平米的房间为50万，100平米的房间为110万，120平米的房间121万，那可以预测一下145平米的房价为多少吗？很简单，我们可以大概拟合出一条直线，x代表面积，y代表房价，这条直线基本穿过这三个样本，那么x为145时，y的值就是我们想要的结果。 这就引出了我们的part1，线性回归

单变量线性回归

• 现在抛出一个问题，现在有三个采集到的样本点，想要用最佳的一条直线去拟合出x与y之间的关系，怎么拟合最好呢？
  如果拟合的结果很好，应该直线正好穿过样本点，也就是相同x下，直线的y值与样本点的y值差距为0.
  

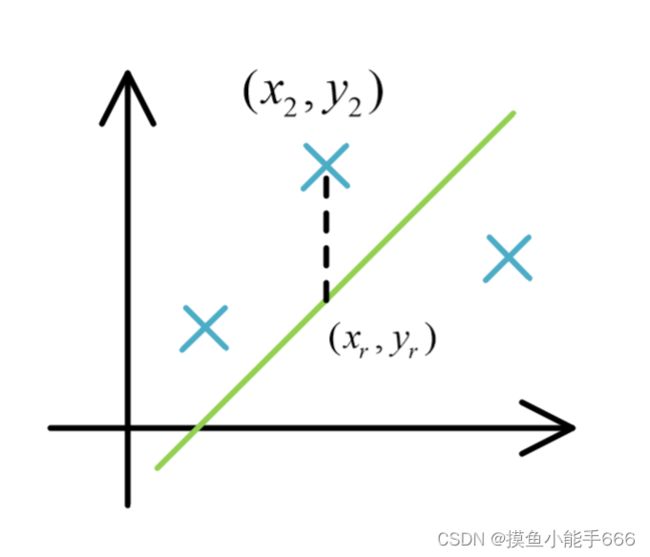
假如我以一条绿色的直线拟合，我们不妨用同样的X下，样本点的y值与直线的y值之间的距离来表示拟合的结果与预期结果的差距，我们用J来表示，第二个点与拟合曲线的距离为

$J=\left|y_2-y_r\right|$

这只是第二个点与直线的距离，如果现在有m个点，总的误差应该是各个点的求和，我们将第 i 个样本表示为$(x^{(i)},y^{(i)})$,拟合的直线上的值使用$h_{\theta }={\theta }_0+{\theta }_1{x}^{(i)}$来表示，那么误差J可以表示为

$J\left({\theta }_0,{\theta }_1\right)=\frac{1}{2m}{\sum }_{i=1}^m{\left({\theta }_0+{\theta }_1{x}^{(i)}-y^{(i)}\right)}^2$

为什么绝对值变成了平方？这是因为绝对值在计算时非常麻烦，将他变成平方可以有效的减少计算时带来的麻烦。为什么前面乘上了1/2m？这个是为了方便求导，平方的求导正好有一个2，和1/2抵消，m是样本个数，除以m是因为有m个求和相加，方便计算。

需要注意的一点是$x^{(i)}和y^{(i)}$为常数，他是我们一个个真实观测到的样本，不是变量。这个式子里面的未知数是${\theta }_0,{\theta }_1$，我们目的是为了求这两个变量，寻找一条最合适的直线来拟合，也就是求误差$J(\theta )$最小，我们称$J(\theta )$为损失函数

下面是求这两个变量的方法

目前这个式子还是有点复杂，我们先假设拟合直线为$h_{\theta }={\theta }_1{x}^{(i)}$

此时

$J\left({\theta }_1\right)=min(\frac{1}{2m}{\sum }_{i=1}^m{\left({\theta }_1{x}^{(i)}-y^{(i)}\right)}^2)$

一般，我们求函数最小值的方法是求导，算出极值点，我们顺着这个一般的思路，先把这个平方项展开，方便求导，他可以化简为

$J\left({\theta }_1\right)=a{\theta }_1^2+b{\theta }_1+c$

这里面的a，b，c等都是未知量，他里面包含着$x^{(i)}和y^{(i)}$等常数。可以看到，损失函数是一个抛物线函数，求他的最低点我们可以通过求导解决，但是这里我们使用一个全新的求最低点的方法：梯度下降，这是一位大佬想出来的方法，他的表达式如下：

${\theta }_1={\theta }_1-\alpha \frac{\partial J(\theta )}{\partial {\theta }_1}$

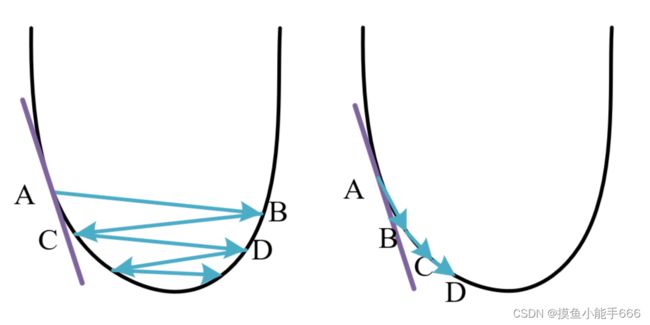
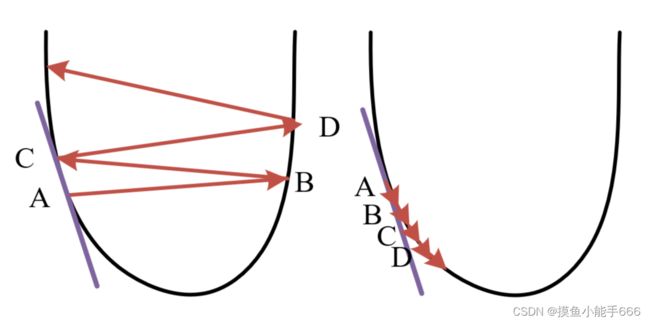
我们想求的${\theta }_1$可以通过等号右边的${\theta }_1$，也就是他自己减去$\alpha$乘以$J(\theta )$的求导，在一个凸函数中，函数的求导代表该点的斜率，假设初始的${\theta }_1$位于点A位置，减去该点的斜率乘以学习率$\alpha$（$\alpha$的大小设置比较小时），可能会落在左图的B点，随着越来越靠近最低点，斜率慢慢减小，移动的距离会慢慢变小，${\theta }_1$会逐渐移动到C，D···直至逼近最低点。如果$\alpha$有点大，那么他就会像右图一样移动，左右震荡慢慢趋近最小值。

仔细观察一下这个梯度下降公式，最低点右边的点的导数，也就是那个点的切线斜率，右边点的切线斜率都过一三象限，所以是正数，减去正数就是自己再往左边靠近了。同理，取到了最低点左边的点，说明取小了，也可以根据这个公式往右边靠近。

可以看到这个方法需要学习率$\alpha$设置比较合适，当它太大时，他会不停的左右震荡，当他过小时，他会收敛的很慢

他是一个非常适合计算机去使用的求最小值的方法，因为计算机可以很快速的完成这样一遍遍的操作，我们只需要设定一个前一轮与后一轮的差值大小为结束标志即可。

刚才我们把拟合简化成$h_{\theta }={\theta }_1{x}^{(i)}$了，现在我们把它还原$h_{\theta }={\theta }_0+{\theta }_1{x}^{(i)}$，看一看一条直线的梯度下降公式是什么样子的。

损失函数：

$J\left({\theta }_1\right)=min(\frac{1}{2m}{\sum }_{i=1}^m{\left({\theta }_0+{\theta }_1{x}^{(i)}-y^{(i)}\right)}^2)$

懒得看计算过程版：经过一系列的计算，我们可以得到${\theta }_0$和${\theta }_1$的梯度下降公式

$\begin{array}{l}{\theta }_0={\theta }_0-\alpha \frac{1}{m}{\sum }_{i=1}^m(h_{\theta }\left(x^{(i)}\right)-y^{(i)})\\ \\ {\theta }_1={\theta }_1-\alpha \frac{1}{m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\cdot x^{(i)}\end{array}$

怎么能不看计算过程呢？你不好奇吗？

梯度下降公式里面需要计算的就是损失函数的求导，我们来分别求导一下

我们将损失函数对${\theta }_0$求导，计算它的梯度下降公式:

$$\begin{gathered} J\left({\theta }_0,{\theta }_1\right)=\frac{1}{2m}{\sum }_{i=1}^m{\left({\theta }_0+{\theta }_1{x}^{(i)}-y^{(i)}\right)}^2 \\ \Rightarrow \frac{\partial J(\theta )}{\partial {\theta }_0}=\frac{1}{m}{\sum }_{i=1}^m\left({\theta }_0+{\theta }_1{x}^{(i)}-y^{(i)}\right) \\ \Rightarrow \frac{\partial J(\theta )}{\partial {\theta }_0}=\frac{1}{m}{\sum }_{i=1}^m\left(h_{\theta }(x^{(i)})-y^{(i)}\right) \end{gathered}$$

带入梯度下降公式即可

我们将损失函数对${\theta }_1$求导，计算它的梯度下降公式:

$$\begin{gathered} J\left({\theta }_0,{\theta }_1\right)=\frac{1}{2m}{\sum }_{i=1}^m{\left({\theta }_0+{\theta }_1{x}^{(i)}-y^{(i)}\right)}^2 \\ \Rightarrow \frac{\partial J(\theta )}{\partial {\theta }_1}=\frac{1}{m}{\sum }_{i=1}^m\left({\theta }_0+{\theta }_1{x}^{(i)}-y^{(i)}\right)x(i) \\ \Rightarrow \frac{\partial J(\theta )}{\partial {\theta }_1}=\frac{1}{m}{\sum }_{i=1}^m\left(h_{\theta }(x^{(i)})-y^{(i)}\right)x(i) \end{gathered}$$

带入梯度下降公式即可。

ok，上面已经说完了单变量线性回归，我们已经学会了损失函数，梯度下降。可是目前我们只能解决单变量线性的回归问题，可是现实生活中，变量并不只一个，例如在预测房价时，变量会出现面积，地区，采光等等，他们都共同影响着预测结果，因此，我们需要多变量线性回归的问题。

多变量线性回归

不妨来挑战一下，写出多变量线性回归的损失函数和梯度下降公式。我们写出直线的表达式：

$h_{\theta }(X)={\theta }_0+{\theta }_1{X}_1+{\theta }_2{X}_2+{\theta }_3{X}_3\cdot \cdot \cdot +{\theta }_n{X}_n$

那么他的损失函数为

$J\left({\theta }_1\cdots {\theta }_n\right)=\frac{1}{2m}{\left({\sum }_{i=1}^n{h}_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)}^2$

我们来计算他的损失函数，先求损失函数的偏导

$\frac{\partial J}{\partial {\theta }_0}=\frac{1}{m}{\sum }_{i=1}^m\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)$

$\frac{\partial J}{\partial {\theta }_1}=\frac{1}{m}{\sum }_{i=1}^m\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)x_1^{(i)}$

这两个求导公式如果在上文认真看过一遍的话是十分简单就算出来的。接着我们算0，1以后的求导

$\frac{\partial J}{\partial {\theta }_j}=\frac{1}{m}{\sum }_{i=1}^m\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)x_j^{(i)}$

他们的表达式都是一样的，我们不在${\theta }_0$后面乘上$X_0$，这个$X_0$的值为1

此时拟合式子的函数表达式为

$h_{\theta }(X)={\theta }_0{X}_0+{\theta }_1{X}_1+{\theta }_2{X}_2+{\theta }_3{X}_3\cdot \cdot \cdot +{\theta }_n{X}_n$

那么

$\frac{\partial J}{\partial {\theta }_0}=\frac{1}{m}{\sum }_{i=1}^m\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)X_0$

这样子所有的偏导式子都一样了，我们用一个式子表达

$\frac{\partial J}{\partial {\theta }_j}=\frac{1}{m}{\sum }_{i=1}^m\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)x_j^{(i)})其中j=0\cdots n$

则梯度下降公式为

${\theta }_j={\theta }_j-\alpha \frac{1}{m}{\sum }_{i=1}^m\left(\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)x_j^{(i)}\right)其中j=0\cdots n$

这个就是多变量线性回归的梯度下降公式，注意下 i 和 j 分别代表什么？i 代表样本个数，共有 m 个样本， j 代表变量 ，共有 n 个变量

至此，我们已经学会了线性回归，梯度下降，损失函数的概念。

在接下来的部分中，我们将会学习逻辑回归，sigmoid函数，交叉熵损失函数，均方误差函数的概念。学完第二个part，我们就可以开始理解BP神经网络了。(期待下一期吧！！)