概率校准及其实现方式

1、什么是概率校准？为什么需要概率校准？

众所周知，对于一个分类模型而言，其主要的任务预测未知样本属于哪个预定义的类别。但在某些场景中，我们不仅希望得到样本的类别标签，也希望知道这样分类的把握有多大。例如，银行在对客户进行评分时，并不满足于识别出该用户是否存在信用风险，更希望能够确定客户存在信用风险的概率，以便计算客户违约带来的期望损失，使得银行能够准备充足的资本以应对风险。¹

我们知道，有一些模型本身的输出可以代表概率，如逻辑回归和朴素贝叶斯模型；但一些复杂的非线性机器学习算法是无法直接进行概率预测的。因此，有必要对分类结果进行再学习以得到概率，这就是通常意义上说的概率校准。

事实上，概率校准不仅能够将非概率分类模型的输出转化为概率，而且也能够对概率分类模型的结果进行进一步修正。例如，在经过概率校准的逻辑回归模型输出的所有概率为0.8的样本中，大约有80%的样本实际上确实属于正例——在校准之前，可能结果并不是这样。

2、如何对模型的输出概率进行评估？

上文说到，概率校准可以对模型输出的概率进行修正。那么首先需要解决的问题是，如何判断一个模型是否需要修正？进一步地，如何对输出概率进行评估以及比较不同的模型之间概率输出的优劣？

一个易于理解的例子是，如果有两个分类器$C_1$和$C_2$，它们分别预测并得到了100个概率为0.8的样本，经过实际验证发现，$C_1$对应的100个样本中真正例共有60个，而$C_2$对应的有70个。直观上，$C_2$更好一些。这是因为从$C_2$的预测结果来看，其真实的预测概率为0.7，相较于$C_1$的0.6而言，更接近理论最优分类器的预测（0.8）。

当理论最优分类器有80%的把握将$n$样本为正类时，那么当$n$足够大时，其中真正例的数量就会是$n\ast 0.8$。

基于上述朴素的想法，在样本充足的情况下，对于任何一个概率值$p$，我们可以得到足够的、属于正例的可能性为$p$的样本，进一步可以知道它们正确的类别标签并算出真正例的占比$T_p$。可以想见，如果收集到足够的$(p,T_p)$数据，那么就可以绘制一条线，这条线就被称为该分类器的校准曲线。

不难想到，理论最优分类器的校准曲线将穿过原点且斜率为1。

校准曲线（Calibration Curves），也被称为可靠性图（Reliability Diagrams），用于直观地表示二分类器做出概率预测时偏离理论最优分类器预测的程度。

由于概率在$[0,1]$区间内的值是连续的，因此，在实际绘制校准曲线图时，往往先进行“分箱”，例如，将其分为10等份。以第一个区间$[0,0.1)$为例，假设一共有$m$个样本被目标分类器以概率$p$（$p\in [0,0.1)$）预测为正例，经过实际验证其中为真正例的数量为$n$，那么，可以得到$T_p=\frac{n}{m}$；分类器对$m$个样本一共输出$m$个概率值，可以求出它们的平均值，记为$\overline{p}$。采用相同的方法，对每个分箱（bin）都求出上述两个值，就可以绘制出该分类器的校准曲线。

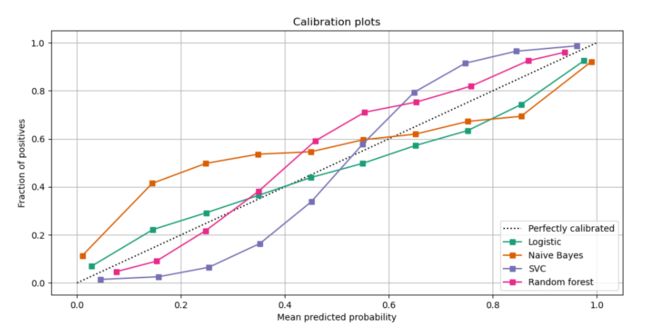
可以将多个分类器的校准曲线绘制在一起，以便于比较它们之间的差异²：

在上图中，中间的虚线是理论最优分类器的曲线，其他分类器的曲线越接近虚线，说明它们的预测结果越好。

如果曲线在虚线上方，说明对当前分类器而言，预测的相对“不自信”（例如，以0.2的概率预测为正类，但实际的结果中正类的比例超过20%）；如果曲线在虚线下方，说明对当前分类器而言，预测的相对“过于自信”（例如，以0.2的概率预测为正类，但实际的结果中正类的比例不足20%）。

3、如何进行概率校准³

在明确了概率校准的概念以及如何评价校准效果后，接下来的任务就是如何进行概率校准。

3.1 概率校准的基本任务

对于那些不直接输出概率或者输出值不能很好地代表概率的分类器而言，在校准之前首先就需要将它们的输出结果进行概率化。我们可以通过一个校准器（calibrator，实际上就是一个回归模型）来完成这项工作，它实际上就是将原始分类器的输出映射成$[0,1]$区间上的一个概率值。假设给定一个样本时原始分类器的输出为$f_i$，那么校准器的工作就是来预测$p(y_i=1|f_i)$。⁴

另外需要注意的是，用来拟合校准器的数据应该与用来训练分类器的数据不同，否则会导致结果偏差。其原因在于：原始分类器在训练集上肯定有比较好的分类效果，这时如果再用相同的数据来拟合校准器，那么其输出概率总是会比预期的更加接近0或1——在了解了下面介绍的校准器的工作原理后，你会知道为什么是这样。

3.2 概率校准的方法

3.2.1 Sigmoid回归

我们知道，sigmoid函数的输出可以很好地代表概率值，因此，可以用它来进行概率校准，这就是所谓的Platt Scaling⁵：

$$p(y_i=1|f_i)=\frac{1}{1+exp(A{f}_i+B)}$$

由此可以看出，校准器的训练过程实际上就是确定参数$A$和$B$的过程，因此，这种方法也被称为参数方法。参数的是通过极大似然估计得到的，具体推导过程这里不再叙述，感兴趣的同学可以参考附录1和附录4。

有的同学可能会疑惑，为啥经过这样的转换之后就实现了概率校准？如何证明校准之后的预测效果按照第2部分给出的评估方法确实要比校准前要好呢？对于这个疑问，Platt给出的解释：这种转换确实可以实现校准，因为他在各种基准数据集上利用SVM分类器（使用常见的核函数）测试过。也就是说，这个结论并不是被严格证明的，而是一个经验结论。

此外，有研究表明，在校准误差是对称的情况下，这种校准方法可以取得非常好的效果，因为这种情况实际上暗示了二分类器的每个输出都以相同的方差呈正态分布⁶。由此也同样可知，如果样本类别高度不平衡，那么这种校准很可能起不到什么作用。

总结来说，当原始分类器的输出属于“相对不自信”的情况，且校准误差在高概率侧和低概率侧相似时，这种方法被证实是有效的。

3.2.2 Isotonic回归

Isotonic回归以原始分类器输出的每个样本的概率为自变量，以该样本的真实标签为因变量，来拟合一个单调递增的函数。它的拟合是通过最小化平方误差实现的：

$$\sum _{i=1}^m(y_i-\widehat{f_i}{)}^2$$

其限制条件为：当$f_i\le f_j$时，总有$\widehat{f_i}\le \widehat{f_j}$。

其中，$y_i$为样本$i$的真实标签，$\widehat{f_i}$是校准后样本$i$的输出概率。

实际上，Sigmoid方法是Isotonic方法的一个特例——Isotonic方法仅要求函数是单调递增的，而并没有限制具体的形式。因此，Isotonic方法也更加强大（对原始预测结果分布的要求上更为宽松），但前提是具有足够的数据，否则它很容易陷入过拟合。

3.2.3 总结

总结来说，在数据量充足的情况下（至少大于1000），Isotonic方法会取得比Sigmoid方法更好（或者至少和其一样好）的结果；否则，为了降低过拟合的风险，还是使用Sigmoid方法。

---

1. 浅谈分类问题中的概率校准 ↩︎

2. Comparison of Calibration of Classifiers ↩︎

3. Probability calibration ↩︎

4. Calibrating a classifier ↩︎

5. Probabilistic Outputs for Support Vector Machines and Comparisons to Regularized Likelihood Methods ↩︎

6. How to obtain well-calibrated probabilities from binary classifiers with beta calibration ↩︎