R语言回归中的Hosmer-Lemeshow以及calibration curve校正曲线
Hosmer-Lemeshow test
详细的Hosmer-Lemeshow test使用方法的介绍请参考:看这里
calibration curve是评价模型的一个重要指标,不信的话请看文章1,文章2,总之很重要的!!!
最近需要画校正曲线,但网上的相关资料实在是太少了,花了点时间研究了一下,跟大家分享一下如何使用Hosmer-Lemeshow test来绘制calibration curve,(p.s. 都是个人理解,可能有错,欢迎讨论):
首先,按照方法介绍中的样例,我们生成一下数据:
set.seed(43657)
n <- 100
x <- rnorm(n)
xb <- x
pr <- exp(xb)/(1+exp(xb))
y <- 1*(runif(n) < pr)
这里的x是变量,y相当于标签(0,1),这里做的是二分类的。然后我们放到glm函数中fit一下:
mod <- glm(y~x, family=binomial)
然后,将结果y和模型拟合概率传递给hoslem.test函数,选择g = 10组。在这之前,要记得先安装并加载package,安装方法为install.paskages(‘ResourceSelection’),加载方法为library(ResourceSelection)。
hl <- hoslem.test(mod$y, fitted(mod), g=10)
hl
这里的mod$y和 fitted(mod)分别表示标签和预测概率,可以换成自己的数据。hl输出为:
Hosmer and Lemeshow goodness of fit (GOF) test
data: mod$y, fitted(mod)
X-squared = 7.4866, df = 8, p-value = 0.4851
我们还可以从hl对象中获得一个观察到的与预期的表:
cbind(hl$observed,hl$expected)
输出为
y0 y1 yhat0 yhat1
[0.0868,0.219] 8 2 8.259898 1.740102
(0.219,0.287] 7 3 7.485661 2.514339
(0.287,0.329] 7 3 6.968185 3.031815
(0.329,0.421] 8 2 6.194245 3.805755
(0.421,0.469] 5 5 5.510363 4.489637
(0.469,0.528] 4 6 4.983951 5.016049
(0.528,0.589] 5 5 4.521086 5.478914
(0.589,0.644] 2 8 3.833244 6.166756
(0.644,0.713] 6 4 3.285271 6.714729
(0.713,0.913] 1 9 1.958095 8.041905
其中y0, y1表示观察的结果,yhat0,yhat2表示预期的结果。为了理解这些数字都代表些什么,我们手动计算一下,首先,我们计算模型的预测概率,然后根据预测概率的十分位数对观察结果进行分组(这里其实就是将模型预测的概率进行排序,然后将数据划分成10组):
pihat <- mod$fitted
pihatcat <- cut(pihat, breaks=c(0,quantile(pihat, probs=seq(0.1,0.9,0.1)),1), labels=FALSE)
接下来,我们循环遍历第1组到第10组,计算观察到的0和1的数量,并计算期望的0和1的数量。
这里提一下,上面我们选择了g=10,那么根据模型拟合出来的概率mod$fitted和十分位数,我们将所有数据分为10组,下面是本例中10组的分组情况,可以看到每个数据在哪个组别:
10 10 9 8 2 9 2 1 6 5 2 1 1 10 5 6 4 4 8 3 6 3 9 2 9 3 6 5 4 7 4 9 3 5 8 4 7 4 3 2 2 8 6 1 3 5 7 2 7 2 8 7 6 1 1 4 8 9 10 10 1 5 1 4 6 9 10 6 7 3 8 2 2 9 5 10 7 6 5 4 7 6 9 1 10 3 3 8 10 7 5 7 10 1 8 8 4 9 3 5
为了计算期望的0和1的数量,我们找到每个组中预测概率的平均值,然后将其乘以组大小,这里为10:
meanprobs <- array(0, dim=c(10,2))
expevents <- array(0, dim=c(10,2))
obsevents <- array(0, dim=c(10,2))
stdprobs <- array(0, dim=c(10,2))
obsprobs <- array(0, dim=c(10,2))
for (i in 1:10) {
meanprobs[i,1] <- mean(pihat[pihatcat==i])
stdprobs[i,1] <- sd(pihat[pihatcat==i])
expevents[i,1] <- sum(pihatcat==i)*meanprobs[i,1]
obsevents[i,1] <- sum(y[pihatcat==i])
obsprobs[i,1] <- sum(y[pihatcat==i])/sum(pihatcat==i)
meanprobs[i,2] <- mean(1-pihat[pihatcat==i])
stdprobs[i,2] <- sd(1-pihat[pihatcat==i])
expevents[i,2] <- sum(pihatcat==i)*meanprobs[i,2]
obsevents[i,2] <- sum(1-y[pihatcat==i])
obsprobs[i,2] <- 1-(sum(y[pihatcat==i])/sum(pihatcat==i))
}
这里meanprobs 表示每组的平均概率,expevents 表示期望事件,obsevents 表示观察事件,我加了两个参数,方便绘制calibration curve,其中,stdprobs 表示每组的标准差,obsprobs 表示每组的观察概率。
然后,我们可以通过上面计算得到的表格的10x2单元格中的(观察到的预期)^ 2 /预期的总和来计算Hosmer-Lemeshow检验统计量:
hosmerlemeshow <- sum((obsevents-expevents)^2 / expevents)
hosmerlemeshow
可以看到输出为:
[1] 7.486643
和hoslem.test函数计算出来的一样对吧。
calibration curve
现在,我们有了观察的概率表obsprobs, 和预测的平均概率meanprobs ,以及预测概率的方差stdprobs,可以绘制calibration curves了。
先绘制一个空图,
yy <- meanprobs[,c(1)]
xx <- obsprobs[,c(1)]
plot(xx, yy, type = "n", xlab = "Predicted probability", ylab = "Oberserved probability")
然后,添加数据,
points(xx, yy, type = "p", pch = 19, col = "seagreen", lty = 1)
通过改变type的值可以选择绘制散点图还是折线图,或者是别的类型的图。然后,我们在图上添加误差棒
plot_error <- function(xx, yy, sd, len = 1, col = "black") {
len <- len * 0.05
arrows(x0 = xx, y0 = yy, x1 = xx, y1 = yy - sd, col = col, angle = 90, length = len)
arrows(x0 = xx, y0 = yy, x1 = xx, y1 = yy + sd, col = col, angle = 90, length = len)
}
plot_error(xx, yy, sd = stdprobs[,c(1)], col = "seagreen")
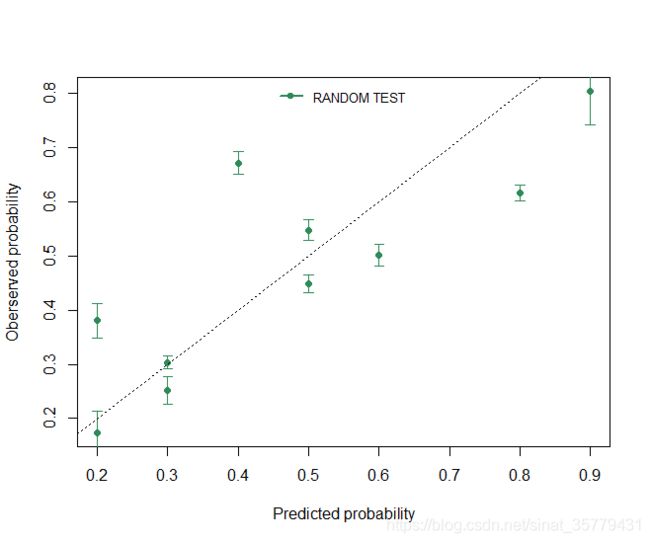
最后,加上对角线和legend,就可以绘制出一张校正曲线图啦。
abline(0,1,lty=3,lwd=1,col=c(rgb(0,0,0,maxColorValue=255)))
labs <- c("RANDOM TEST")
legend("top", legend = labs, cex = 0.8, lty = 1, lwd = 2, pch = 19, col = c("seagreen"), inset = 0.01, horiz = TRUE, box.col = "white")
P.S 这里使用的是简单的glm模型来做模型得到的概率,如果有现成的概率和标签,也是可以直接绘制calibration curve的~