【图像特征提取与匹配】ORB算法详述
ORB算法
ORB(Oriented FAST and Rotated BRIEF)特征是目前看来非常具有代表性的实时图像特征。它改进了 FAST(Features from Accelerated Segment Test) 检测子不具有方向性的问题,并采用速度极快的二进制描述子BRIEF(Binary Robust Independent Elementary Features),使整个图像特征提取的环节大大加速。
ORB 特征亦由关键点和描述子两部分组成。它的关键点称为“Oriented FAST”,是一种改进的 FAST 角点,什么是 FAST 角点我们将在下文介绍。它的描述子称为BRIEF。因此,提取 ORB 特征分为两个步骤:
(1) FAST 角点提取:找出图像中的“角点”。相较于原版的 FAST, ORB 中计算了特征点的主方向,为后续的 BRIEF 描述子增加了旋转不变特性。
(2) BRIEF 描述子:对前一步提取出特征点的周围图像区域进行描述。
1关键点提取(Oriented FAST)
FAST是一种角点,主要检测局部像素灰度变化明显的地方,以速度快著称。它的思想是:如果一个像素与它邻域的像素差别较大(过亮或过暗) , 那它更可能是角点。相比于其他角点检测算法,FAST只需比较像素亮度的大小,十分快捷。检测过程如下。
(1) 在图像中选取像素 p,假设它的亮度为 Ip。
(2) 设置一个阈值 T (比如 Ip 的 20%)。
(3) 以像素 p 为中心, 选取半径为 3 的圆上的 16 个像素点。
(4) 假如选取的圆上,有连续的 N 个点的亮度大于 Ip + T 或小于 Ip − T,那么像素 p可以被认为是特征点 (N 通常取 12,即为 FAST-12。其它常用的 N 取值为 9 和 11,他们分别被称为 FAST-9, FAST-11)。
(5) 循环以上四步,对每一个像素执行相同的操作。
在 FAST-12 算法中,为了更高效,可以添加一项预测试操作,以快速地排除绝大多数不是角点的像素。具体操作为,对于每个像素,直接检测邻域圆上的第 1, 5, 9, 13 个像素的亮度。只有当这四个像素中有三个同时大于 Ip + T 或小于 Ip − T 时,当前像素才有可能是一个角点,否则应该直接排除。这样的预测试操作大大加速了角点检测。此外,原始的 FAST 角点经常出现“扎堆”的现象。所以在第一遍检测之后,还需要用非极大值抑制(Non-maximal suppression),在一定区域内仅保留响应极大值的角点,避免角点集中的问题。
FAST 特征点的计算仅仅是比较像素间亮度的差异,速度非常快,但它也有一些问题。首先, FAST 特征点数量很大且不确定,而我们往往希望对图像提取固定数量的特征。因此,在 ORB 中,对原始的 FAST 算法进行了改进。我们可以指定最终要提取的角点数量N,对原始 FAST 角点分别计算 Harris 响应值,然后选取前 N 个具有最大响应值的角点,作为最终的角点集合。
其次, FAST 角点不具有方向信息。而且,由于它固定取半径为 3 的圆,存在尺度问题:远处看着像是角点的地方,接近后看可能就不是角点了。针对 FAST 角点不具有方向性和尺度的弱点, ORB 添加了尺度和旋转的描述。尺度不变性由构建图像金字塔,并在金字塔的每一层上检测角点来实现。而特征的旋转是由灰度质心法(Intensity Centroid)实现的。
质心是指以图像块灰度值作为权重的中心。其具体操作步骤如下:
(1) 在一个小的图像块 B 中,定义图像块的矩为:
(2) 通过矩可以找到图像块的质心:
(3) 连接图像块的几何中心 O 与质心 C,得到一个方向向量,于是特征点的方向可以定义为:
通过以上方法, FAST 角点便具有了尺度与旋转的描述,大大提升了它们在不同图像之间表述的鲁棒性。所以在 ORB 中,把这种改进后的 FAST 称为 Oriented FAST。BRIEF 描述子
2 BRIEF描述子
BRIEF 是一种二进制描述子,它的描述向量由许多个 0 和 1 组成,这里的 0 和 1 编码了关键点附近两个像素(比如说 p 和 q)的大小关系:如果 p 比 q 大,则取 1,反之就取 0。所有的点对都进行比较,则生成长度为n的二进制串。一般n取128、256或512,opencv默认为256。具体步骤如下。
(1) 以特征点P为中心,取一个S×S大小的Patch邻域;
(2) 在这个邻域内随机取N对点,然后对这2×N点分别做高斯平滑(高斯分布即为正态分布),以防描述符对高频噪点过于敏感。定义τ测试,比较N对像素点的灰度值的大小;
(3) 最后把步骤2得到的N个二进制码串组成一个N维向量即可;
关于做τ测试前,需要对随机点做高斯平滑,由于采用单个的像素灰度值做比较,会对噪声很敏感;采用高斯平滑图像,会降低噪声的影响,使得描述子更加稳定。论文中建议采用9×9的pixels。
论文中对随机取N对点采用了5中不同的方法做测试,论文中建议采用G II的方法:
G I :(X,Y)~(-S/2,S/2)分布,X,Y即均匀分布;
G II: X,Y均服从(0,S平方/25)高斯分布;
G III: X服从(0,S平方/25)高斯分布,Y服从(Xi,S平方/100)高斯分布,先随机取X点,再以X点为中心,取Y点;
G V: X固定在中心,在Patch内,Y在极坐标系中尽可能取所有可能的值;
G V: X固定在中心,在Patch内,Y在极坐标系中尽可能取所有可能的值。
3缩放不变性(图像金字塔)和旋转不变性(BRIEF改进)
3.1缩放不变性(图像金字塔)
图像金字塔是单个图像的多尺度表示法,由一系列原始图像的不同分辨率版本组成。金字塔的每个级别都由上个级别的图像下采样版本组成。下采样是指图像分辨率被降低,比如图像按照 1/2 比例下采样。因此一开始的 4x4 正方形区域现在变成 2x2 正方形。图像的下采样包含更少的像素,并且以 1/2 的比例降低大小。
这是一个包含 5 个级别的图形金字塔示例,在每个级别图像都以 1/2 的比例下采样。到了第四级别图像的分辨率是原始图像的 1/16。ORB 创建好图像金字塔后,它会使用 FAST 算法从每个级别不同大小的图像中快速找到关键点。因为金字塔的每个级别由原始图像的更小版本组成,因此原始图像中的任何对象在金字塔的每个级别也会降低大小。
通过确定每个级别的关键点 ORB 能够有效发现不同尺寸的对象的关键点,这样的话 ORB 实现了部分缩放不变性。这一点很重要,因为对象不太可能在每个图像中的大小都完全一样。
现在 ORB 获得了与这个图像金字塔每个级别相关的关键点。在发现金字塔所有级别中的关键点后,ORB 现在为每个关键点分配一个方向(oFAST),例如朝左或朝右,取决于该关键点周围的强度是如何变化的。
为金字塔级别 0 的图像中的每个关键点分配方向后,ORB 现在为所有其他金字塔级别的图像重复相同流程。需要注意的是,在每个图像金字塔级别,Patch 大小并没有缩减,因此相同 Patch 在每个金字塔级别覆盖的图像区域将更大,导致关键点的大小各不相同。
可以从此处看出这一点。在此图中,圆圈表示每个关键点的大小,更高的金字塔级别中的关键点大小更大。
3.2 Steered BRIEF(旋转不变性改进)
在使用oFast算法计算出的特征点中包括了特征点的方向角度。假设原始的BRIEF算法在特征点SxS(一般S取31)邻域内选取n对点集。
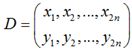
经过旋转角度θ旋转,得到新的点对
![]()
在新的点集位置上比较点对的大小形成二进制串的描述符。
![]()
这里需要注意的是,在使用oFast算法是在不同的尺度上提取的特征点。因此,在使用BRIEF特征描述时,要将图像转换到相应的尺度图像上,然后在尺度图像上的特征点处取SxS邻域,然后选择点对并旋转,得到二进制串描述符。
3.3 rBRIEF-改进特征点描述子的相关性
使用steered BRIEF方法得到的特征描述子具有旋转不变性,但是却在另外一个性质上不如原始的BRIEF算法。是什么性质呢,是描述符的可区分性,或者说是相关性(可区分性越大,相关性越小)。这个性质对特征匹配的好坏影响非常大。描述子是特征点性质的描述。描述子表达了特征点不同于其他特征点的区别。我们计算的描述子要尽量的表达特征点的独特性。如果不同特征点的描述子的可区分性比较差,匹配时不容易找到对应的匹配点,引起误匹配。ORB论文中,作者用不同的方法对100k个特征点计算二进制描述符,对这些描述符进行统计,如下表所示:
我们先不看rBRIEF的分布。对BRIEF和steered BRIEF两种算法的比较可知,BRIEF算法落在0上的特征点数较多,因此BRIEF算法计算的描述符的均值在0.5左右,每个描述符的方差较大,可区分性较强。而steered BRIEF失去了这个特性。至于为什么均值在0.5左右,方差较大,可区分性较强的原因,这里大概分析一下。这里的描述子是二进制串,里面的数值不是0就是1,如果二进制串的均值在0.5左右的话,那么这个串有大约相同数目的0和1,那么方差就较大了。用统计的观点来分析二进制串的区分性,如果两个二进制串的均值都比0.5大很多,那么说明这两个二进制串中都有较多的1时,在这两个串的相同位置同时出现1的概率就会很高。那么这两个特征点的描述子就有很大的相似性。这就增大了描述符之间的相关性,减小之案件的可区分性。
下面我们介绍解决上面这个问题的方法:rBRIEF。
原始的BRIEF算法有5种取点对的方法,原文作者使用了方法G II。为了解决描述子的可区分性和相关性的问题,ORB论文中没有使用5种方法中的任意一种,而是使用统计学习的方法来重新选择点对集合。
首先建立300k个特征点测试集。对于测试集中的每个点,考虑其31x31邻域。这里不同于原始BRIEF算法的地方是,这里在对图像进行高斯平滑之后,使用邻域中的某个点的5x5邻域灰度平均值来代替某个点的灰度值,进而比较点对的大小。这样特征值更加具备抗噪性。另外可以使用积分图像加快求取5x5邻域灰度平均值的速度。
从上面可知,在31x31的邻域内共有(31-5+1)x(31-5+1)=729个这样的子窗口,那么取点对的方法共有M=265356种,我们就要在这M种方法中选取256种取法,选择的原则是这256种取法之间的相关性最小(区别度大)。怎么选取呢?
(1) 在300k特征点的每个31x31邻域内按M种方法取点对,比较点对大小,形成一个300kxM的二进制矩阵Q。矩阵的每一列代表300k个点按某种取法得到的二进制数。
(2) 对Q矩阵的每一列求取平均值,按照平均值到0.5的距离大小重新对Q矩阵的列向量排序,形成矩阵T。
(3) 将T的第一列向量放到R中。
(4) 取T的下一列向量和R中的所有列向量计算相关性,如果相关系数小于设定的阈值,则将T中的该列向量移至R中。
(5) 按照(4)的方式不断进行操作,直到R中的向量数量为256。
总结
ORB算法最大的特点就是计算速度快,计算时间大概只有SIFT的1%,SURF的10%,这主要是因为使用了FAST来加速了特征点的提取。其次是使用BRIEF算法计算描述子,该描述子特有的2进制串的表现形式不仅节约了存储空间,而且大大缩短了匹配的时间。同时具有旋转不变性和一定的尺度不变性,但其尺度变换的应对能力比较低。
代码:
static Ptr<ORB> cv::ORB::create ( int nfeatures = 500,
float scaleFactor = 1.2f,
int nlevels = 8,
int edgeThreshold = 31,
int firstLevel = 0,
int WTA_K = 2,
int scoreType = ORB::HARRIS_SCORE,
int patchSize = 31, //此参数是用来设置特征点领域覆盖的大小
int fastThreshold = 20 )
Ptr<ORB>orb1 = ORB::create(500,1.2f,8,31,0,2,ORB::HARRIS_SCORE,31,20);
orb1->detectAndCompute(img, //提取特征描述符的图片
Mat(), //
img_points, //特征点
orb_descriptors, //输出的特征描述符
false); //是否使用预先设置好的特征点,true代表使用,false代表不使用。
Ptr<DescriptorMatcher> matcher_1 = DescriptorMatcher::create("BruteForce-Hamming");//定义特征匹配器,定位特征匹配方式为暴力汉明法
std::vector<DMatch> orb_matchMap;//定义匹配特征对容器
matcher_1->match(ORB_descriptors_match,ORB_descriptors_map, orb_matchMap, Mat());//进行特征匹配
//注:orb特征描述符进行匹配的时候,输出的是海明距离,海明距离是整数.