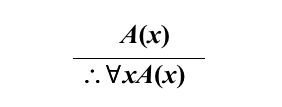06 第五章 一阶逻辑等值演算与推理
离散数学与组合数学汇总
文章目录
- 5.1 一阶逻辑等值式与置换规则
-
- 等值式
- 置换规则、换名规则、代替规则
- 5.2 一阶逻辑前束范式
- 5.3 一阶逻辑的推论理论
-
- 推理定律
- 量词消去引入规则
- 自然推理系统N~L~
主要内容
- 一阶逻辑等值式与基本的等值式
- 置换规则、换名规则、代替规则
- 前束范式
- 自然推理系统NL及其推理规则
5.1 一阶逻辑等值式与置换规则
等值式
定义5.1 设A, B是两个谓词公式, 如果A↔B是永真式, 则称A与B等值, 记作A⇔B, 并称A⇔B是等值式
基本等值式
第一组 命题逻辑中16组基本等值式的代换实例
例如,¬¬∀xF(x)⇔∀xF(x),
∀xF(x)→∃yG(y)⇔¬∀xF(x)∨∃yG(y) 等
第二组
(1) 消去量词等值式
设D ={a1, a2, … , an}
① ∀xA(x) ⇔A(a1)∧A(a2)∧…∧A(an)
② ∃xA(x) ⇔ A(a1)∨A(a2)∨…∨A(an)
(2) 量词否定等值式
① ¬∀xA(x) ⇔ ∃x ¬A(x)
② ¬∃xA(x) ⇔ ∀x ¬A(x)
(3) 量词辖域收缩与扩张等值式.
A(x) 是含 x 自由出现的公式,B 中不含 x 的自由出现
关于全称量词的:
① ∀x(A(x)∨B) ⇔ ∀xA(x)∨B
② ∀x(A(x)∧B) ⇔ ∀xA(x)∧B
③ ∀x(A(x)→B) ⇔ ∃xA(x)→B
④ ∀x(B→A(x)) ⇔ B→∀xA(x)
关于存在量词的:
① ∃x(A(x)∨B) ⇔∃xA(x)∨B
② ∃x(A(x)∧B) ⇔ ∃xA(x)∧B
③ ∃x(A(x)→B) ⇔ ∀xA(x)→B
④ ∃x(B→A(x)) ⇔ B→∃xA(x)
(4) 量词分配等值式
① ∀x(A(x)∧B(x)) ⇔ ∀xA(x)∧∀xB(x)
② ∃x(A(x)∨B(x)) ⇔ ∃xA(x)∨∃xB(x)
注意:∀对∨,∃对∧无分配律
置换规则、换名规则、代替规则
1. 置换规则
设Φ(A)是含A的公式, 那么, 若A⇔B, 则Φ(A)⇔Φ(B).
2. 换名规则
设A为一公式,将A中某量词辖域中个体变项的所有约束
出现及相应的指导变元换成该量词辖域中未曾出现过的个
体变项符号,其余部分不变,设所得公式为A’,则A’⇔A.
3. 代替规则
设A为一公式,将A中某个个体变项的所有自由出现用A中
未曾出现过的个体变项符号代替,其余部分不变,设所得
公式为A’,则A’⇔A.
5.2 一阶逻辑前束范式
定义5.2 设A为一个一阶逻辑公式,若A具有如下形式
Q1x1Q2x2…QkxkB
则称A为前束范式,其中Qi (1<= i <=k)为∀或∃,B为不含量词
的公式.
定理5.1(前束范式存在定理)
一阶逻辑中的任何公式都存在与之等值的前束范式
5.3 一阶逻辑的推论理论
推理的形式结构
- A1∧A2∧…∧Ak →B
若次式是永真式, 则称推理正确, 记作A1∧A2∧…∧Ak =>B - 前提: A1, A2,…, Ak
结论: B
推理定理: 永真式的蕴涵式
推理定律
第一组 命题逻辑推理定理的代换实例
如, ∀xF(x)∧∃yG(y) ⇒ ∀xF(x)
第二组 基本等值式生成的推理定理
如, ∀xF(x) ⇒ ¬¬∀xF(x), ¬¬∀xF(x) ⇒ ∀xF(x)
¬∀xF(x) ⇒ ∃x¬F(x), ∃x¬F(x) ⇒ ¬∀xF(x)
第三组 其他常用推理定律
(1) ∀xA(x)∨ ∀xB(x) ⇒ ∀x(A(x)∨B(x))
(2) ∃x(A(x)∧B(x)) ⇒ ∃xA(x)∧∃xB(x)
(3) ∀x(A(x)→B(x)) ⇒ ∀xA(x)→∀xB(x)
(4) ∃x(A(x)→B(x)) ⇒ ∃xA(x)→∃xB(x)
量词消去引入规则
其中x,y是个体变项符号, c是个体常项符号, 且在A中x不在∀y
和 ∃y的辖域内自由出现.
- 全称量词引入规则(∀+)
其中x是个体变项符号, 且不在前提的任何公式中自由出现
其中x是个体变项符号, 且不在前提的任何公式和B中自由
出现
其中x,y是个体变项符号, c是个体常项符号, 且在A中y和c不在
∀x和∃x的辖域内自由出现.
自然推理系统NL
定义5.3 自然推理系统NL 定义如下:
- 字母表. 同一阶语言L的字母表
- 合式公式. 同L 的合式公式
- 推理规则:
(1) 前提引入规则
(2) 结论引入规则
(3) 置换规则
(4) 假言推理规则
(5) 附加规则
(6) 化简规则
(7) 拒取式规则
(8) 假言三段论规则
(9) 析取三段论规则
(10) 构造性二难推理规则
(11) 合取引入规则
(12) ∀-规则
(13) ∀+规则
(14) ∃-规则
(15) ∃+规则
重要提示
要特别注意使用∀-、∀+、∃-、∃+规则的条件.
反例1. 对A=∀x∃yF(x,y)使用∃-规则, 推得B=∃yF(y,y).

反例2. 前提: P(x)→Q(x), P(x)
结论: ∀xQ(x)

“证明”:
① P(x)→Q(x) 前提引入
② P(x) 前提引入
③ Q(x) ①②假言推理
④ ∀xQ(x) ③∀+
错误原因: 在④使用∀+规则, 而x在前提的公式中自由出现.