np.dot、np.outer、np.matmul、np.multipy、np.inner、np.outer与np.cross几个函数之间的区别
np.dot、np.outer、np.matmul、np.multipy、np.inner、np.outer与np.cross几个函数之间的区别
- 一、数学上关于【内积】、【外积】的定义和计算
-
- 1.1 数学上关于【内积/数量积】的定义和计算
- 1.2 数学上关于【外积/叉积】的定义和计算
- 二、numpy中关于np.dot、np.outer、np.matmul、np.multipy、np.inner、np.outer与np.cross几个函数之间的区别
-
- 2.1、np.dot()函数
- 2.2 numpy.outer()计算两个向量的外积
- 2.3. np.matmul()计算两个矩阵的乘积
- 2.4. np.multiply()计算两数组各对应位置对应元素的乘积
- 2.5. 运算符“*”在numpy中的应用
- 2.5 np.cross()计算两个数组或向量的叉积
一、数学上关于【内积】、【外积】的定义和计算
1.1 数学上关于【内积/数量积】的定义和计算
向量的点乘,也叫做向量的内积、数量积。对两个向量执行点乘运算,就是对着两个向量对应位置一一相乘之后求和的操作,点乘的结果是一个标量。
定义: 两个向量 a a a 与 b b b 的内积为 a ∙ b = ∣ a ∣ ∣ b ∣ c o s ∠ ( a , b ) a\bullet b = |a||b|cos∠(a, b) a∙b=∣a∣∣b∣cos∠(a,b),特别地, 0 ∙ a = a ∙ 0 = 0 0\bullet a =a\bullet 0 = 0 0∙a=a∙0=0;若 a , b a,b a,b是非零向量,则 a a a 与 b b b 正交的充要条件是 a ∙ b = 0 a \bullet b = 0 a∙b=0。
点乘公式
对于向量 a a a 和向量 b b b:
a = [ a 1 , a 2 , . . . , a n ] 和 b = [ b 1 , b 2 , . . . , b n ] a=[a_1,a_2,...,a_n]和b=[b_1,b_2,...,b_n] a=[a1,a2,...,an]和b=[b1,b2,...,bn]
a a a 和 b b b 的点乘公式:
a ∙ b = a T b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + . . . a n b n \mathbf{a}\bullet\mathbf{b}=\mathbf{a}^T\mathbf{b}=\sum_{i=1}^na_ib_i=a_1b_1+a_2b_2+...a_nb_n a∙b=aTb=i=1∑naibi=a1b1+a2b2+...anbn
要求:一维向量 a a a 和向量 b b b 的行列数相同。
点乘的几何意义:
可以用来表征或计算两个向量之间的夹角,以及在b向量在a向量方向上的投影,有公式:
a ∙ b = ∣ a ∣ ∣ b ∣ c o s θ a\bullet b=|a||b|cos\theta a∙b=∣a∣∣b∣cosθ
根据这个公式就可以计算向量a和向量b之间的夹角。从而就可以进一步判断这两个向量是否是同一方向,是否正交(也就是垂直)等方向关系,具体对应关系为:
- a ∙ b > 0 a\bullet b>0 a∙b>0,方向基本相同,夹角在0°到90°之间;
- a ∙ b = 0 a\bullet b=0 a∙b=0,正交,相互垂直;
- a ∙ b < 0 a \bullet b<0 a∙b<0,方向基本相反,夹角在90°到180°之间。
向量点乘的运算特性:
- a 2 ≥ 0 a^2 ≥ 0 a2≥0;当 a 2 = 0 a^2 = 0 a2=0时,必有 a = 0 a = 0 a=0; (正定性)
- a ∙ b = b ∙ a ; a\bullet b = b\bullet a; a∙b=b∙a;(对称性)
- ( λ a + μ b ) ∙ c = λ a ∙ c + μ b ∙ c (λa + μb)\bullet c = λa\bullet c + μb\bullet c (λa+μb)∙c=λa∙c+μb∙c,对任意实数 λ , μ λ, μ λ,μ成立; (线性)
- c o s ∠ ( a , b ) = a ∙ b / ( ∣ a ∣ ∣ b ∣ ) cos∠(a,b) =a\bullet b/(|a||b|) cos∠(a,b)=a∙b/(∣a∣∣b∣);
- ∣ a ⋅ b ∣ ≤ ∣ a ∣ ∣ b ∣ |a·b| ≤ |a||b| ∣a⋅b∣≤∣a∣∣b∣,等号只在 a a a与 b b b共线时成立。
1.2 数学上关于【外积/叉积】的定义和计算
两个向量的叉乘,又叫向量积、外积、叉积,叉乘的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量组成的坐标平面垂直。
定义: 向量 a a a 与 b b b 的外积 a × b a×b a×b 是一个向量,其长度等于 ∣ a × b ∣ = ∣ a ∣ ∣ b ∣ s i n ∠ ( a , b ) |a×b| = |a||b|sin∠(a,b) ∣a×b∣=∣a∣∣b∣sin∠(a,b),其方向正交于 a a a与 b b b。并且,向量 ( a , b , a × b ) (a, b, a×b) (a,b,a×b)构成右手系。
对于向量 a a a 和向量 b b b:
a = ( x 1 , y 1 , z 1 ) a=(x_1,y_1,z_1) a=(x1,y1,z1)
b = ( x 2 , y 2 , z 2 ) b=(x_2,y_2,z_2) b=(x2,y2,z2)
a a a 和 b b b 的叉乘公式:
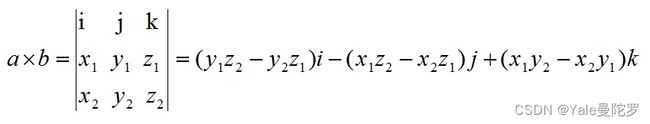
其中, i = ( 1 , 0 , 0 ) , j = ( 0 , 1 , 0 ) , k = ( 0 , 0 , 1 ) i=(1,0,0)\quad, j=(0,1,0)\quad ,k=(0,0,1)\quad i=(1,0,0),j=(0,1,0),k=(0,0,1)
根据 i , j , k i,j,k i,j,k 之间的关系,有:
a × b = ( y 1 z 2 − y 2 z 1 , − ( x 1 z 2 − x 2 z 1 ) , x 1 y 2 − x 2 y 1 ) \mathbf{a}×\mathbf{b}=(y_1z_2-y_2z_1,-(x_1z_2-x_2z_1),x_1y_2-x_2y_1) a×b=(y1z2−y2z1,−(x1z2−x2z1),x1y2−x2y1)
叉乘的几何意义:
- 在三维几何中,向量 a a a 和向量 b b b 的叉乘结果是一个向量,更为熟知的叫法是【法向量】,该向量垂直于 a a a 和 b b b 向量构成的平面。
叉乘的运算特性:
- b × a = − a × b b×a=-a×b b×a=−a×b(反称性)
- 特别地, 0 × a = a × 0 = 0 0×a = a×0 = 0 0×a=a×0=0;此外,对任意向量 a a a, a × a = 0 a×a=0 a×a=0。
- ( λ a + μ b ) × c = λ ( a × c ) + μ ( b × c ) (λa + μb) × c = λ(a ×c) + μ(b ×c) (λa+μb)×c=λ(a×c)+μ(b×c) (线性)。
在3D图像学中,叉乘的概念非常有用,可以通过两个向量的叉乘,生成第三个垂直于a,b的法向量,从而构建X、Y、Z坐标系。如下图所示:
插图参考链接:矩阵外积与内积
-
在二维空间中,叉乘还有另外一个几何意义就是: a × b = a×b= a×b= 由向量 a a a 和向量 b b b 构成的平行四边形的面积。
-
一个行向量乘以一个列向量称作向量的【内积】,又叫做【点积】,结果是一个数;
-
一个列向量乘以一个行向量称作向量的【外积】,结果是一个矩阵;
假设 a T a^T aT 和 b b b 分别是一个行向量和一个列向量,那么内积、外积分别记作 a T ⋅ b a^T·b aT⋅b 和 b ⊗ a T b \otimes a^T b⊗aT ,为了方便讨论,假设每个向量的长度为2。
a T ⋅ b = a 1 b 1 + a 2 b 2 a^T·b=a_1b_1+a_2b_2 aT⋅b=a1b1+a2b2
b ⊗ a T = ( b 1 a 1 b 1 a 2 b 2 a 1 b 2 a 2 ) (2) b \otimes a^T=\left( \begin{matrix} b_1a_1 & b_1a_2\\ b_2a_1 & b_2a_2 \\ \end{matrix} \right) \tag{2} b⊗aT=(b1a1b2a1b1a2b2a2)(2)
二、numpy中关于np.dot、np.outer、np.matmul、np.multipy、np.inner、np.outer与np.cross几个函数之间的区别
2.1、np.dot()函数
numpy.dot(a, b, out=None)两个数组的点积。
np.dot()计算规则:np.dot(a, b, out=None):
- 若 a a a, b b b 为一维(1-D维)数组,则 a ∙ b a\bullet b a∙b = 向量的内积;
- 若 a a a, b b b 为二维(2-D维)数组,则 a ∙ b a\bullet b a∙b = 矩阵的乘法(等效于
矩阵乘法函数matmul(a,b)或者a@b); - 若 a a a 或 b b b 为零维(0-D维)数组(即:标量),则 a ∙ b a\bullet b a∙b = 逐元素的乘法(等效于
两数组对应位的元素相乘multiply(a,b)或者a*b); - 若 a a a 为 n n n 维(n-D维)数组,且 b b b 是 1 1 1 维(1-D维)数组,则 a ∙ b a\bullet b a∙b = a a a 的最后一个轴向与 b b b 的乘积和;
- 若 a a a 为 n n n 维(n-D维)数组,且 b b b 是 M M M 维(M-D维)数组(其中 M > = 2 M>=2 M>=2),则 a ∙ b a\bullet b a∙b = a a a 的最后一个轴向与 b b b 的倒数第二个轴向的乘积和。
备注:在情形⑤中, d o t ( a , b ) dot(a, b) dot(a,b)的结果满足如下公式:
d o t ( a , b ) [ i , j , k , m ] = s u m ( a [ i , j , : ] ∗ b [ k , : , m ] ) dot(a, b)[i,j,k,m] = sum(a[i,j,:] * b[k,:,m]) dot(a,b)[i,j,k,m]=sum(a[i,j,:]∗b[k,:,m])
注意事项: 如果 a a a 的最后一个维度与 b b b 的倒数第二个维度的大小不同,则在计算 d o t ( a , b ) dot(a, b) dot(a,b) 时,将报错ValueError。
一、一维数组
np.dot(3, 4)
>>>
12
np.dot([2, 3], [4, 4])
>>>
20
二、二维数组
a = [[1, 0], [0, 1]]
b = [[4, 1], [2, 2]]
np.dot(a, b)
>>>
array([[4, 1],
[2, 2]])
三、n维数组
a = np.arange(6).reshape(1, 2, 3)
b = np.arange(6).reshape(2, 3, 1)
a
>>>
array([[[0, 1, 2],
[3, 4, 5]]])
b
>>>
array([[[0],
[1],
[2]],
[[3],
[4],
[5]]])
# 计算n维数组数组的点积
np.dot(a, b)
>>>
array([[[[ 5],
[14]],
[[14],
[50]]]])
2.2 numpy.outer()计算两个向量的外积
numpy.outer(a, b, out=None)计算两个向量的外积。
np.outer()表示的是两个向量相乘,拿第一个向量的元素分别与第二个向量所有元素相乘得到结果的一行。
给定两个向量, a = [ a 0 , a 1 , . . . , a M ] a = [a_0, a_1, ..., a_M] a=[a0,a1,...,aM] 和 b = [ b 0 , b 1 , . . . , b N ] b = [b_0, b_1, ..., b_N] b=[b0,b1,...,bN] ,np.outer(a,b)输出:
[[a0*b0 a0*b1 ... a0*bN ]
[a1*b0 .
[ ... .
[aM*b0 aM*bN ]]
参数:
-
a(m,)数组
第一个输入向量。如果输入不是一维的,则将被展平。 -
b(n)
第二输入向量。如果输入不是一维的,则将被展平。 -
out(m,n)ndarray,可选。
np.outer(a,b)输出满足: o u t [ i , j ] = a [ i ] ∗ b [ j ] out[i, j] = a[i] * b[j] out[i,j]=a[i]∗b[j]
典型范例:
import numpy as np
lr = np.outer(np.ones((5,)),np.linspace(-2,2,5))
lr
>>>
array([[-2., -1., 0., 1., 2.],
[-2., -1., 0., 1., 2.],
[-2., -1., 0., 1., 2.],
[-2., -1., 0., 1., 2.],
[-2., -1., 0., 1., 2.]])
其中,
np.ones((5,))
>>>
array([1., 1., 1., 1., 1.])
np.linspace(-2,2,5)
>>>
array([ 2., 1., 0., -1., -2.])
im = np.outer(1j*np.linspace(2,-2,5),np.ones((5,)))
im
>>>
array([[0.+2.j, 0.+2.j, 0.+2.j, 0.+2.j, 0.+2.j],
[0.+1.j, 0.+1.j, 0.+1.j, 0.+1.j, 0.+1.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.-1.j, 0.-1.j, 0.-1.j, 0.-1.j, 0.-1.j],
[0.-2.j, 0.-2.j, 0.-2.j, 0.-2.j, 0.-2.j]])
其中,
1j*np.linspace(2,-2,5) # 可将【1j】看做一个【有系数项的向量】,【*np.linspace(2,-2,5)】相当于改变该向量的【系数项】
>>>
array([ 0.+2.j, 0.+1.j, 0.+0.j, -0.-1.j, -0.-2.j])
grid = lr + im
grid
>>>
array([[-2.+2.j, -1.+2.j, 0.+2.j, 1.+2.j, 2.+2.j],
[-2.+1.j, -1.+1.j, 0.+1.j, 1.+1.j, 2.+1.j],
[-2.+0.j, -1.+0.j, 0.+0.j, 1.+0.j, 2.+0.j],
[-2.-1.j, -1.-1.j, 0.-1.j, 1.-1.j, 2.-1.j],
[-2.-2.j, -1.-2.j, 0.-2.j, 1.-2.j, 2.-2.j]])
# 使用字母”矢量“的示例:
np.outer(np.array(['a','b','c']), [1,2,3])
>>>
x = np.array(['a','b','c'], dtype=object)
x
>>>
array(['a', 'b', 'c'], dtype=object) # 备注:np.array(['a','b','c'])输出:array(['a', 'b', 'c'], dtype='
np.outer(x, [1,2,3])
>>>
array([['a', 'aa', 'aaa'],
['b', 'bb', 'bbb'],
['c', 'cc', 'ccc']], dtype=object)
参考链接:官方教程numpy.outer(a, b, out=None)
2.3. np.matmul()计算两个矩阵的乘积
np.matmul( X 1 , X 2 X_1, X_2 X1,X2, out=None)计算两个数组的矩阵乘积。
给定两个数组, X 1 = ( n , k ) X_1 = (n,k) X1=(n,k) 和 X 2 = ( k , m ) X_2 = (k,m) X2=(k,m) ,np.outer(a,b)输出:
参数:
- X 1 , X 2 X_1,X_2 X1,X2为array_like,是输入数组,不允许使用标量。
- o u t out out为 n − D n-D n−D维数组,可选。
X 1 , X 2 X_1,X_2 X1,X2与 o u t out out的shape必须满足如下关系: ( n , k ) , ( k , m ) → ( n , m ) (n,k),(k,m)→(n,m) (n,k),(k,m)→(n,m);只有当 X 1 , X 2 X_1,X_2 X1,X2都是一维向量时, o u t out out才是一个标量。
备注:执行np.matmul( X 1 , X 2 X_1, X_2 X1,X2)时,如果 X 1 X_1 X1)的最后一个维度与 X 2 X_2 X2 的倒数第二个维度不同,则报错ValueError。
a = np.ones([9, 5, 7, 4])
c = np.ones([9, 5, 4, 3])
np.dot(a, c).shape
>>>
(9, 5, 7, 9, 5, 3)
np.matmul(a, c).shape
>>>
(9, 5, 7, 3)
# n is 7, k is 4, m is 3
2.4. np.multiply()计算两数组各对应位置对应元素的乘积
np.matmul( X 1 , X 2 X_1, X_2 X1,X2, out=None)计算对应元素的乘积。
np.matmul( X 1 , X 2 X_1, X_2 X1,X2) 结果等价于 x 1 ∗ x 2 x1 * x2 x1∗x2 的阵列广播。
参数:
- X 1 , X 2 X_1,X_2 X1,X2为array_like,是要相乘的输入数组;
如果 x1.shape != x2.shape ,它们必须根据广播运算规则扩展至公共形状方可(成为输出的形状)。
- o u t out out为 n − D n-D n−D数组,如果提供,它必须具有输入广播后的形状。如果未提供或没有,则返回新分配的数组。
np.multiply(2.0, 4.0)
>>>
8.0
x1 = np.arange(9.0).reshape((3, 3))
x2 = np.arange(3.0)
np.multiply(x1, x2)
>>>
array([[ 0., 1., 4.],
[ 0., 4., 10.],
[ 0., 7., 16.]])
等价运算
x1 = np.arange(9.0).reshape((3, 3))
x2 = np.arange(3.0)
x1 * x2
>>>
array([[ 0., 1., 4.],
[ 0., 4., 10.],
[ 0., 7., 16.]])
2.5. 运算符“*”在numpy中的应用
运算符*表示对于元素的乘积,必须满足 numpy 的 broadcasting(广播) 的原则 。 当两个矩阵相乘时,其法则为两矩阵的对应的元素相乘,其用法与np.multiply()相同。
备注:关于numpy中广播的计算规则,参考我的另一篇博文——numpy的广播机制的计算原理详解
典型范例:
例1:矩阵 a*b 相乘,其中 a 为 3*4,b 为 1*4;
a = np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12]])
b = np.array([1,2,3,4])
c = a*b
print(c)
>>>
[[ 1 4 9 16]
[ 5 12 21 32]
[ 9 20 33 48]]
例2:矩阵 a,b 相乘,其中 a 为 3*4,b 为 3*1;
import numpy as np
a = np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12]])
d = np.array([[1],[2],[3]])
e = a*d
print(e)
>>>
[[ 1 2 3 4]
[10 12 14 16]
[27 30 33 36]]
2.5 np.cross()计算两个数组或向量的叉积
np.cross(a, b, axisa=- 1, axisb=- 1, axisc=- 1, axis=None)计算两个数组或向量的叉积
几何含义: 数组或向量a 和 b的叉积 np.cross(a,b)表示的是垂直于两向量 a、b所在平面的法向量 。
np.cross(a, b)的结果满足 a a a 和 b b b 的叉乘公式:
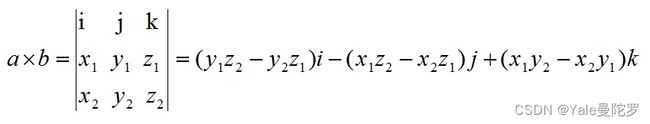
其中, i = ( 1 , 0 , 0 ) , j = ( 0 , 1 , 0 ) , k = ( 0 , 0 , 1 ) i=(1,0,0)\quad, j=(0,1,0)\quad ,k=(0,0,1)\quad i=(1,0,0),j=(0,1,0),k=(0,0,1)
根据 i , j , k i,j,k i,j,k 之间的关系,有:
a × b = ( y 1 z 2 − y 2 z 1 , − ( x 1 z 2 − x 2 z 1 ) , x 1 y 2 − x 2 y 1 ) \mathbf{a}×\mathbf{b}=(y_1z_2-y_2z_1,-(x_1z_2-x_2z_1),x_1y_2-x_2y_1) a×b=(y1z2−y2z1,−(x1z2−x2z1),x1y2−x2y1)
x = [1, 2, 3]
y = [4, 5, 6]
np.cross(x, y)
>>>
array([-3, 6, -3])
参考链接:官方教程numpy.cross
