Python中的优先队列(priority queue)和堆(heap)

目录

• 队列和优先队列（Priority Queue）
• 堆（heap）
• 简介
• 初始化构建堆
• 堆的插入（节点上浮）
• 堆的删除(节点下浮)
• 堆的应用

队列和优先队列（Priority Queue）

队列是一种可以完成插入和删除的数据结构。普通队列是先进先出（FIFO), 即先插入的先被删除。

然而在某些时候我们需要按照任务的优先级顺序来决定出队列的顺序，这个时候就需要用到优先级队列了。优先队列是一种可以完成插入和删除最小元素的数据结构

python中有现成的优先队列类可以调用。

代码示例

from queue import Queue   # 队列，FIFO
from queue import PriorityQueue  #优先级队列，优先级高的先输出
###############队列（Queue）的使用，/python中也可是用列表（list）来实现队列###############
q = Queue(maxsize) 	#构建一个队列对象，maxsize初始化默认为零，此时队列无穷大
q.empty()		#判断队列是否为空(取数据之前要判断一下)
q.full()		#判断队列是否满了
q.put()			#向队列存放数据
q.get()			#从队列取数据
q.qsize()		#获取队列大小，可用于判断是否满/空
###用法示例：
>>> q = Queue(3)
>>> for i in range(3):
>>>	q.put(i)
>>> q.full()
True
>>> while not q.empty():
>>> 	print(q.get())
0
1
2
###############优先队列（PriorityQueue）的使用###############
"""
队列的变体，按优先级顺序（最低优先）检索打开的条目。
条目通常是以下格式的元组：
插入格式：q.put((priority number, data))
特点：priority number 越小，优先级越高
其他的操作和队列相同
"""
>>> q = PriorityQueue()
>>> q.put((2, "Lisa"))
>>> q.put((1, "Lucy"))
>>> q.put((0, "Tom"))
>>> i = 0
>>> while i < q.qsize()：
>>> 	print(q.get())
(0，"Tom")
(1，"Lucy")
(2，"Lisa")
#可见并没有按照输入的顺序输出的，而是按照优先级顺序输出的
#优先独队列的实质是

堆（heap）

看完上面的示例我们也许会有疑惑，优先队列是如何来实现的了？

----------优先队列的实质是每次插入时按照一定的规则插入，删除时直接找到最小的那个元素弹出即可。插入和弹出最坏情况下的时间复杂度都是O(LogN)

下面我们就来介绍实现优先队列的一种数据结构——堆(heap)。

简介

堆的实质是一个完全二叉树(除最底层外，其余层都是满二叉树，且最底层的节点从左往右顺序排列)。 堆主要分为大顶堆和小顶堆两种

1.大顶堆：每个分支的根节点都大于等于其子节点。（ki >= k2i）and (ki >= k2i+1)

2.小顶堆：每个分支的根节点都小于等于其子节点。（ki <= k2i）and (ki <= k2i+1)

所以堆中的第i个元素的父亲是floor(i/2)（向下取整）, 第i个元素的左右孩子分别是2i和2i+1

堆的根节点要从1开始计算，不能从0开始计算。(假如从零开始i=2时其父亲节点为floor(2/2)=1, 显然是错误的)

初始化构建堆

将一个有k个元素的数组构成一个大顶堆或者小顶堆。时间复杂度O(n)$

核心思路：从下往上，从右往左，且每次都从第floor(k/2)个元素开始进行调整依次递减直到根节点

1.从floor(k/2)个元素开始进行调整，调整完毕，则i--；
    #调整节点，每次只调整该根节点以下的子树
    while i <= k
        1.1 找出左右孩子中最大的那个
        1.2 该节点和较大的那个子节点比较，
                如果父节点较大，break
                如果子节点较大，记录子节点的索引，把子节点的值给父节点
        1.3 将上面较大的那个字节点作为新的父节点开始一轮循环
    循环结束后，将父节点的值放到他应该去的子节点的位置上

例如有如下数组

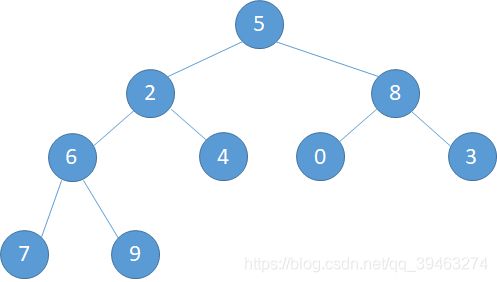
把其转化成完全二叉树的形式就是

该数组一共有9个元素，所以从i = floor(9/2)=4 个元素开始，第4个元素是6, 其右孩子9最大，将6和9交换完成一次调整.

i=3,第三个元素是8,8比左右孩子都大，不用交换

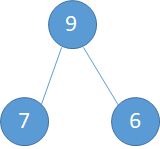
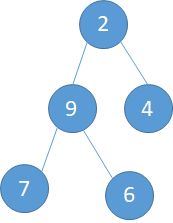
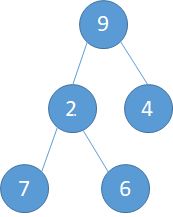
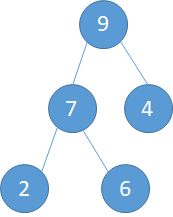
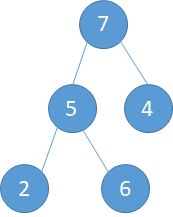
i=2,此时的子树是：第二个元素是2,而此时以2为根节点的子树如下左图。交换过程为: a).2与9交换，此时的根节点就到了2现在的位置 (下中图)。b).2与7交换。 c)交换完成，本次调整完毕

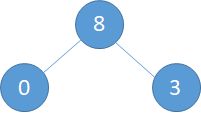
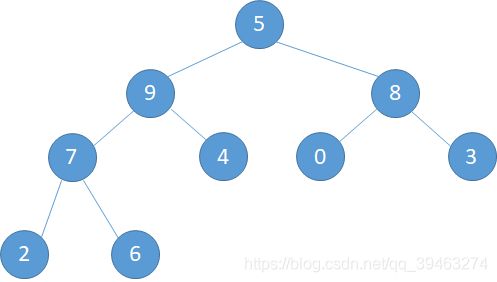
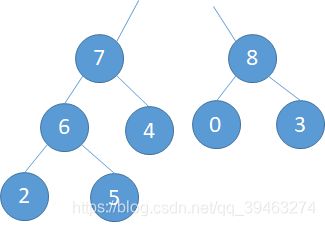
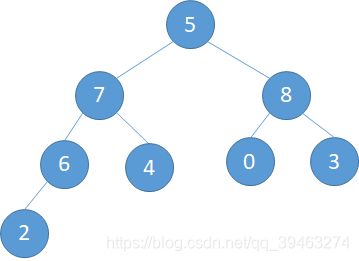
i=1,此时的父节点就是整棵树的根节点,而此时整棵树的状态是下图所示

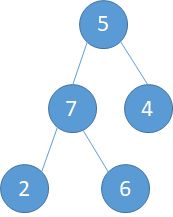
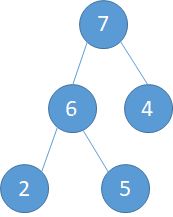
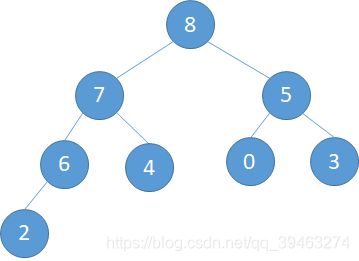
a). 5和9交换，此时5到了9的位置(下左图) b). 5和7交换，5到了7的位置(下中图) c).最后5和6交换，完成调整。

经过以上的floor(k/2)次的调整之后，由一个无序数组初始化构建大顶堆就完成了

堆的插入（节点上浮）

时间复杂度O(log(k+1))

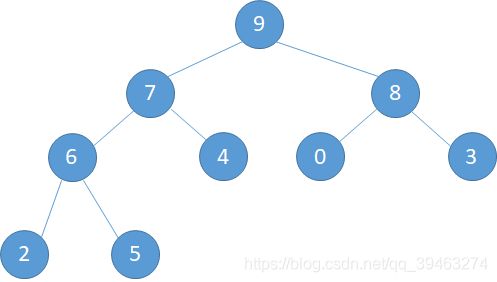
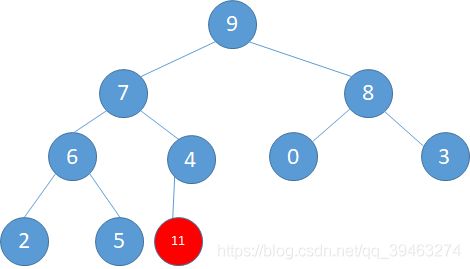
我们之前由一个无序数组构造了一个大顶堆，那么现在我们要插入一个新的元素该怎么办了，如下图，如果直接在最末尾插入，则破坏了堆的结构，所以还需要按进行调整。

调整规则：由于其他子树的顺序都已经调整完毕，所以只需要调整根节点到插入节点所在的子路即可。

如下图所示。(a)将11与4调整，(b)将11与7调整，©再将11与9调整。最后得到调整完毕的结果。

堆的删除(节点下浮)

时间复杂度O(log(k-1))

由于堆是队列结构，只能从堆中删除堆顶的元素。移除堆顶元素之后，之前的完全二叉树就变成来两个子树，次数最方便的做法就是用堆的最后一个节点来填补取走的堆顶元素，并将堆的实际元素个数减1。但是这样做以后又不满足堆的定义了，还是要进行调整。

调整规则：从根节点开始逐层向下调整即可。

（a).将5与8调换，(b)调整完成，删除完毕

堆的应用

之间讲过的利用堆(python中是小顶堆)来实现优先队列

利用堆求Top k：

假如现在有1亿个数据要求其中前十个最小的元素。最笨方法就是对所有数据进行排序，然后找出前十个最小的，即使使用快排，也需要O(NlogN)的时间复杂度。假如利用大顶堆的话–先利用前10个数据构造一个大顶堆，然后顺序遍历数组与大顶堆顶点比较，假如比大于等于顶点直接删除，否则就删除堆顶点并插入新的节点，最后堆里面的元素就是最小的前是个元素。这样求出来的时间复杂度为Nlog(k)

假如要求前十个最大的元素，那就要使用小顶堆来实现

最后放上python手动实现将数组转化为大顶堆和小顶堆的代码

class Heap:
	def __init__(self, _list):
		self._list = _list
		self.k = len(_list)
		
	def _bigHeapAdjuest(self, j):
		temp = self._list[j] #存放当前双亲节点的值,j代表当前节点的位置
		i = 2*j  			 #j的左孩子
		while i <= self.k:
			if i < self.k and self._list[i] < self._list[i+1]:  #i==n时由于只有一个子节点，所以没有比较的必要
				i += 1
			#与双亲比较，如果双亲大则跳过
			#如果双亲小，就把大的给双亲
			if temp >= self._list[i]:
				break                 			#没有必要修整
			self._list[j] = self._list[i]       #元素交换
			j = i                               #j记录着temp应该去的位置,由于这个位置的节点发生了变动，所以需要再次调整
			i *= 2             					#接着找该节点的左孩子
		self._list[j] = temp	
	
    def _smallheapAdjuest(self, j):
        temp = self._list[i] #父节点
        i = 2*j  #左孩子
        while i <= self.k:
            if i < self.k and self._list[i] > self._list[i+1]:    #找最小的那个孩子
                i += 1
            #构建小顶堆，小于父节点的都要上浮
            if self._list[i] >= temp:
                break
            self._list[j] = self._list[i]  #子节点交给父节点
            j= i    #记录父节点应该去的索引位置
            i *= 2
        self._list[j] = temp
	
	def heapSort(self):
		self._list.insert(0, -1) 
		s = self.length // 2  
		#构建大顶堆
		for j in range(s, 0, -1):
			self._bigHeapAdjuest(j) 
		#构建小顶堆
			for j in range(s, 0, -1):
			self._SmallheapAdjuest(j) 
		

以上为个人经验，希望能给大家一个参考，也希望大家多多支持脚本之家。