RL 笔记(2) 从Pollicy Gradient、DDPG到 A3C

RL 笔记(2) 从Pollicy Gradient、DDPG到 A3C

Pollicy Gradient

Policy Gradient不通过误差反向传播，它通过观测信息选出一个行为直接进行反向传播。 通过更新 Policy Network 来直接更新策略的。实际上就是一个神经网络，输入是状态，输出直接就是动作（不是Q值）。而是利用reward奖励直接对选择行为的可能性进行增强和减弱，好的行为会被增加下一次被选中的概率，不好的行为会被减弱下次被选中的概率。一般输出有两种方式：一种是概率的方式，即输出某一个动作的概率；另一种是确定性的方式，即输出具体的某一个动作举例如下图所示：输入当前的状态，输出action的概率分布，选择概率最大的一个action作为要执行的操作

如果要更新 Policy Network 策略网络，或者说要使用梯度下降的方法来更新网络，需要有一个目标函数，对于所有强化学习的任务来说，其实目标都是使所有带衰减 reward 的累加期望最大。
$$L(\theta )=E(r_1+\gamma r_2+{\gamma }^2{r}_3+\dots |\pi (,\theta ))$$
这个损失函数和 Policy Network 策略网络简直没有什么直接联系，reward是环境给出的，跟参数 θ 没有直接运算上的关系。那么该如何能够计算出损失函数关于参数的梯度 ∇θL(θ)?

现在有一个 Policy Network 策略网络，输入状态，输出动作的概率。然后执行完动作之后，我们可以得到reward，或者result。那么这个时候，自然有个非常简单的想法：如果某一个动作得到reward多，那么就使其出现的概率增大，如果某一个动作得到的reward少，那么我们就使其出现的概率减小。

当然，用 reward 来评判动作的好坏是不准确的，甚至用 result 来评判也是不准确的（因为无论是 reward，还是result 都依赖于一连串的动作来达成，不能只将功劳或过错归于当前的动作上。但是这样给了一个新的思路：如果能够构造一个好的动作评判指标，来判断一个动作的好与坏，那么我们就可以通过改变动作的出现概率来优化策略！

假设这个评价指标是 f(s,a), 我们的 Policy Network 输出的 π(a|s,θ)是概率, 那么可以通过极大似然估计的方法来优化这个目标。比如说我们可以构造如下目标函数
$$L(\theta )=\sum log\pi (a|s,\theta )f(s,a)$$
比如说，对于某局游戏，假如最终赢了，那么认为这局游戏中每一步都是好的，如果输了，那么认为都是不好的。好的 f(s,a) 就是1，不好的就是-1，然后极大化上面的目标函数即可。

那么问题就是 f(s,a) 值是对动作好坏最好的评价吗？

显然不是。最理想的状态是对于好的动作 f(s,a) 值为正，对于不好的动作 f(s,a) 值为负。而我们一般 f(s,a) 值并没办法完全达到这种理想状态，会有偏差。实际上，这是Policy Gradient最大的问题，我们很难确定一个最合理的评价指标，也因此，Policy Gradient的 f(s,a) 可以有各种形式：

论文[1]中指出可以使用reward，使用Q，使用A，使用TD来作为动作的评价指标。

那么这些方法中有什么差别呢？归根到底就是variance和bias的问题。

用reward来作为动作的评价是最直接的，采用上图第3种做法reward-baseline是很常见的一种做法。这样做bias比较低，但是variance很大，也就是reward值太不稳定，会导致训练不会。

那么采用Q值会怎样呢？Q值是对reward的期望值，使用Q值variance比较小，bias比较大。一般我们会选择使用A，Advantage。A=Q-V，是一个动作相对当前状态的价值。本质上V可以看做是baseline。对于上图第3种做法，也可以直接用V来作为baseline。但是还是一样的问题，A的variance比较大。为了平衡variance和bias的问题，使用TD会是比较好的做法，既兼顾了实际值reward，又使用了估计值V。在TD中，TD(lambda)平衡不同长度的TD值，会是比较好的做法。也因此，在[1]中提出的general advantage estimation中：
$$A=TD(\lambda )-V$$
那么在实际使用中，需要根据具体的问题选择不同的方法。有的问题reward很容易得到，有的问题reward非常稀疏。reward越稀疏，也就越需要采用估计值。

以上就是Policy Gradient的核心做法。那么要说明的一点是Policy Gradient能够处理不可微的问题。以AlphaGo为例，AlphaGo的policy network输出的是softmax概率，我们只能从中选择一个下法，然后得到一个reward。这种情况下reward和policy network之间是不可微的关系，而使用Policy Gradient则没有这个障碍。也因为Policy Gradient的这个特点，目前的很多传统监督学习的问题因为输出都是softmax的离散形式，都可以改造成Policy Gradient的方法来实现，调节得当效果会在监督学习的基础上进一步提升。

Actor Critic

Actor-Critic 的 Actor 的前生是 Policy Gradients, 这能让它毫不费力地在连续动作中选取合适的动作, 而 Q-learning 做这件事会瘫痪. 那为什么不直接用 Policy Gradients 呢? 原来 Actor Critic 中的 Critic 的前生是 Q-learning 或者其他的 以值为基础的学习法 , 能进行单步更新, 而传统的 Policy Gradients 则是回合更新, 也就是要到一轮结束后才能进行更新。如某盘游戏，假如最后的结果是胜利了，那么可以认为其中的每一步都是好的，反之则认为其中的每一步都是不好的，这降低了学习效率。

要采用单步更新，意味着我们需要为每一步都即时做出评估。Actor-Critic 中的 Critic 负责的就是评估这部分工作，而 Actor 则是负责选择出要执行的动作。这就是 Actor-Critic 的思想。从Actor Critic的命名我们也可以更好的理解Policy Gradient。Actor就是policy network，用来输出动作，而Critic对应value network，就是评价动作用的，通过Critic来引导Actor的更新。从上面论文中提出的各种评价指标可知，看到 Critic 的输出有多种形式，可以采用 Q值、V值 或 TD 等。

因此 Actor-Critic 的思想就是从 Critic 评判模块(采用深度神经网络居多)得到对动作的好坏评价，然后反馈给 Actor(采用深度神经网络居多) 让 Actor 更新自己的策略。从具体的训练细节来说，Actor 和 Critic 分别采用不同的目标函数进行更新， 如可参考这里的代码 Actor-Critic (Tensorflow)，下面要说的 DDPG 也是这么做的。

Deterministic Policy Gradient

还有一类应用神经网络的输出是连续的量，比如机器人控制。那么对于连续控制的问题，我们就无法直接使用policy gradient了，因为aciton不是概率，而是一个具体的向量。这个时候可以使用Deterministic Policy Gradient[2]来实现，基本的思想就是Policy Network的目标就是最大化Q值：
$$loss=-Q$$
就是这么简单。简单之中，这个想法却非常直接。因为我们希望Policy Network越来越好，目标就是希望reward最大化，而reward最大化将会带来Q值最大化。因此，我们让Policy Network的训练目标就是最大化Q值非常合理。那么Q值的计算显然我们还需要构造一个Q Network来实现。这样整个网络就是完全可微的。也就是说Actor是a=A(s)，其中A是Actor网络，s是输入状态，a是输出，Critic是Q=C(s,a)，其中C是Critic网络。那么Actor网络的损失函数loss=-Q=-C(s,a)。所以我们可以发现，Actor网络使用Critic网络作为损失函数。

DDPG

DDPG 相对于 DPG 的核心改进是引入了 Deep Learning，采用深度神经网络作为 DPG 中的策略函数 μμ 和 QQ 函数的模拟，即 Actor 网络和 Critic 网络；然后使用深度学习的方法来训练上述神经网络。两者的关系类似于 DQN 和 Q-learning 的关系。

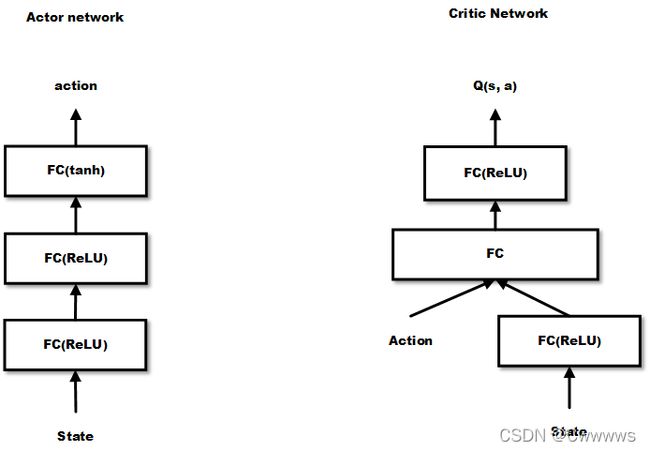
DDPG 的网络结构为 Actor 网络 + Critic 网络，对于状态 s, 先通过 Actor 网络获取 action a, 这里的 a 是一个向量；然后将 a 输入 Critic 网络，输出的是 Q 值，目标函数就是极大化 Q 值，但是更新的方法两者又有一些区别。论文中显示 DDPG 算法流程如下

从算法的流程可知，Actor 网络和 Critic 网络是分开训练的，但是两者的输入输出存在联系，Actor 网络输出的 action 是 Critic 网络的输入，同时 Critic 网络的输出会被用到 Actor 网路进行反向传播。

算法中actor和critic均用DNN表示，分为称为actor network和critic network。它们分别是deterministic policy $\mu$和value-action function $Q$的函数近似，参数分别为${\theta }^Q$ 和${\theta }^{\mu }$ 。在维度比较低时，有下面的结构：

在迭代更新过程中，先积累experience replay buffer直到达到minibatch指定个数，然后根据sample分别更新两个DNN。先更新critic，通过loss函数$L$ 更新参数${\theta }^Q$ 。然后，通过critic得到$Q$ 函数相对于动作$a$ 的梯度，因为在actor的更新公式（也就是DPG定理）中会用到，然后应用actor更新公式更新参数。刚才得到的${\theta }^{\mu }$和${\theta }^Q$ ，对于$\theta$的更新，会按比例（通过参数$\tau$）更新到target network。这个target network会在下一步的训练中用于predict策略和$Q$ 函数值。

A3C

在提出 DDPG 后，DeepMind 在这个基础上提出了效果更好的 Asynchronous Advantage Actor-Critic（A3C）[3]。

传统经验认为，online的RL算法在和DNN简单结合后会不稳定。主要原因是观察数据往往波动很大且前后sample相互关联。像Neural fitted Q iteration和TRPO方法通过将经验数据batch，或者像DQN中通过experience replay memory对之随机采样，这些方法有效解决了前面所说的两个问题，但是也将算法限定在了off-policy方法中。本文提出了另一种思路，即通过创建多个agent，在多个环境实例中并行且异步的执行和学习。于是，通过这种方式，在DNN下，解锁了一大批online/offline的RL算法（如Sarsa, AC, Q-learning）。它还有个潜在的好处是不那么依赖于GPU或大型分布式系统。A3C可以跑在一个多核CPU上。总得来说，这篇论文更多是工程上的设计和优化。另外，将value function的估计作为baseline可以使得PG方法有更低的variance。

这篇文章将one-step Sarsa, one-step Q-learning, n-step Q-learning和advantage AC扩展至多线程异步架构。注意这几种方法特点迥异，AC是on-policy的policy搜索方法，而Q-learning是off-policy value-based方法。这也体现了该框架的通用性。简单地说，每个线程都有agent运行在环境的拷贝中，每一步生成一个参数的梯度，多个线程的这些梯度累加起来，一定步数后一起更新共享参数。

它有几个显著优点：

1）它运行在单个机器的多个CPU线程上，而非使用parameter server的分布式系统，这样就可以避免通信开销和利用lock-free的高效数据同步方法（Hogwild!方法）。

2）多个并行的actor可以有助于exploration。在不同线程上使用不同的探索策略，使得经验数据在时间上的相关性很小。这样不需要DQN中的experience replay也可以起到稳定学习过程的作用，意味着学习过程可以是on-policy的。其它好处包括更少的训练时间，另外因为不需要experience replay所以可以使用on-policy方法（如Sarsa），且能保证稳定。

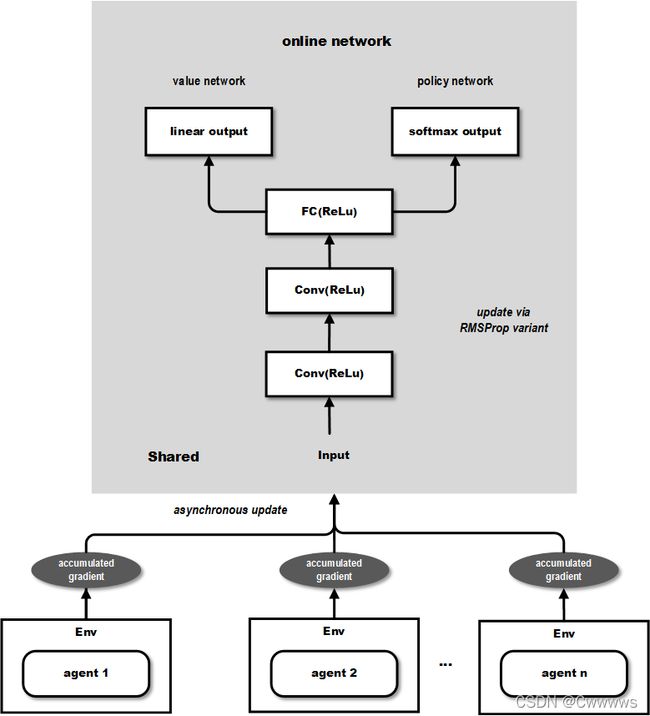
A3C 算法和DDPG类似，通过 DNN 拟合 policy function 和 value function的估计。但是不同点在于：

1. A3C 中有多个 agent 对网络进行 asynchronous update，这样带来了样本间的相关性较低的好处，因此 A3C 中也没有采用 Experience Replay 的机制；这样 A3C 便支持 online 的训练模式了；
2. A3C 有两个输出，其中一个 softmax output 作为 policy $\pi (a_t|s_t;\theta )$，而另一个linear output为 value function $V(s_t;{\theta }_v)$
3. A3C 中的Policy network 的评估指标采用的是上面比较了多种评估指标的论文中提到的 Advantage Function(即A值) 而不是 DDPG 中单纯的 Q 值。

参考

1. 莫烦python
2. DRL之Policy Gradient, Deterministic Policy Gradient与Actor Critic
3. 深度增强学习（DRL）漫谈 - 从AC（Actor-Critic）到A3C（Asynchronous Advantage Actor-Critic）
4. 深度解读：Policy Gradient，PPO及PPG

参考论文：

[1] Schulman, John, et al. “High-dimensional continuous control using generalized advantage estimation.” arXiv preprint arXiv:1506.02438 (2015).

[2] Lillicrap, Timothy P., et al. “Continuous control with deep reinforcement learning.” arXiv preprint arXiv:1509.02971 (2015).

[3] Mnih, Volodymyr, et al. “Asynchronous methods for deep reinforcement learning.” International Conference on Machine Learning. 2016.
P., et al. “Continuous control with deep reinforcement learning.” arXiv preprint arXiv:1509.02971 (2015).

[3] Mnih, Volodymyr, et al. “Asynchronous methods for deep reinforcement learning.” International Conference on Machine Learning. 2016.