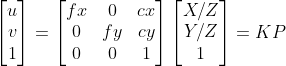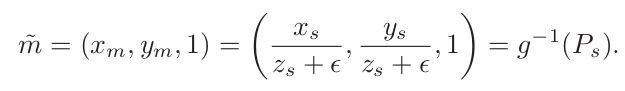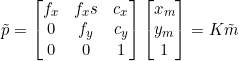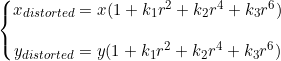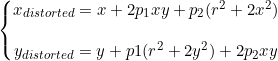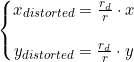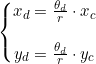hxslam_

相机的成像模型(Pinhole + Omni)和畸变模型(RanTan, FOV, EQUI)

总述

相机将三维世界中的点投影到二维图像平面坐标系的过程可以用几何模型描述，这种模型有很多，相机采用什么模型根据其镜头、相机视野来确定。采用不同的模型其相机也会有不同的称呼如MEI,ANTA相机。这里相机模型主要分为两种——相机成像模型和畸变模型。

【特别说明:本文是通过相关论文、书籍和博客整理而来，文章中的图片和某些语句也是直接翻译引用过来,如果存在侵权行为请联系本人。也是特别感谢这些作者和文献让我能够更快理解到相关知识，另外文中存在表述错误欢迎沟通交流~，若需转载请告知本人】

总述

一、相机成像模型

1.1 针孔模型，参数[fx, fy, cx, cy]

1.2全向模型，参数[, fx, fy, cx, cy]

二、相机畸变模型

2.1、切向径向畸变(RadTan，radial-tangential distortion)

2.2视野畸变(FOV,field of view)

2.3等距畸变(Equidistant,EQUI)

三、特殊的相机名称(MEI, Pinhole,Atan)

参考文献

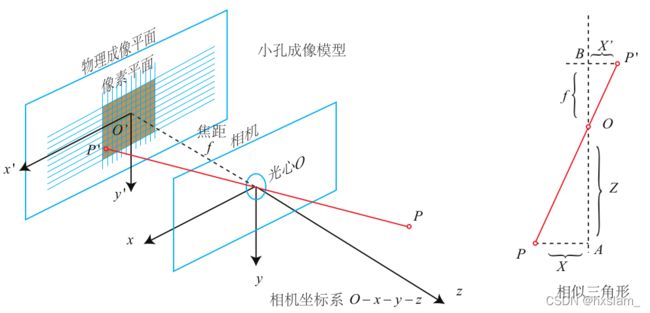
相机成像模型主要包括针孔模型(pinhole model)和全向模型(omnidirectional model)，其中我们熟悉的针孔模型是基于初中物理的小孔成像的原理，即一束光线通过针孔后，会在针孔背面投影成像。大多数商业相机可以使用 pinhole 相机模型来描述，使用一个 perspective projection 来建模。但是存在一些高畸变成像设备如广角相机，建模要考虑透镜反射或者鱼眼镜头折射，它们不能使用传统小孔相机模型来描述。需要使用全向模型进行投影。这里广角相机指的是在一个水平面有360度视野的相机，或视野能覆盖半个球或近似整个球的相机。目前存在几种构建广角相机的方法。如图1所示

1.Dioptric cameras 使用一组 shaped lenses（如鱼眼镜头），可以得到大于180度视野，（稍微多余半球）；

2.Catadioptric cameras 则使用一个标准相机和一个 shaped mirror — such as a parabolic, hyperbolic, or elliptical mirror，其在水平面可以提供360度视野，仰角方向大于100度；这里mirrior type可以通过矫正系数 $\epsilon$ 值来表示，其中矫正系数 $\epsilon$ 的值可以通过透镜圆锥焦点到正焦弦l的距离d这两个参数得到，如表1所示。这个值在后续投影方程中会使用，针孔模型对应Perspective的透镜类型，其矫正系数 $\epsilon$ 值为0。其对应图中红色圆圈所对应的值。

3.polydioptric camera 通过组合多个相机来重叠相机视野[1]。

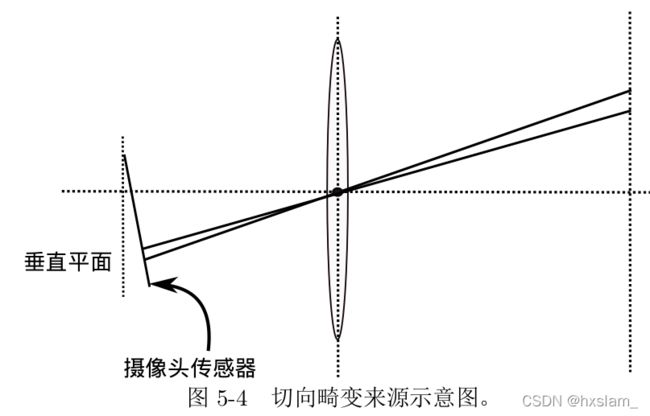
同时为了获得更好的成像效果，我们会在相机前方加了透镜，导致光线投影到成像平面的过程会产生畸变，这一过程需要采用畸变模型去描述，畸变模型主要包括切向径向畸变(RadTan，radial-tangential distortion)、视野畸变(FOV,field of view)和等距畸变(Equidistant,EQUI)等。接下来将分别介绍相机成像模型和畸变模型

一、相机成像模型

1.1 针孔模型，参数[fx, fy, cx, cy]

在相机坐标系o-xyz下有一个空间点P(X,Y,X),通过光心后在物理成像平面上得到成像点，然后通过比例缩放和偏移得到最终的像素平面上的点p(u,v)。其中fx,fy为成像缩放参数 ，cx,cy为成像偏移参数，它们一起组成了相机的内参矩阵 K，也是我们在平时使用相机过程需要去标定的参数。

$\large \begin{bmatrix}u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix} fx &0 &cx \\ 0& fy& cy\\ 0& 0& 1 \end{bmatrix} \begin{bmatrix} X/Z\\ Y/Z\\ 1 \end{bmatrix} = KP$

1.2全向模型，参数[ $\epsilon$ , fx, fy, cx, cy]

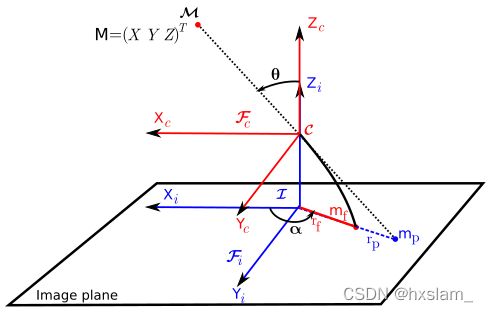
首先将空间点P投影到单位球面上,因此有

$P_{s} = \frac{P}{\left \| P \right \|} = (x_{s}, y_{s},z_{s})$

然后将该点的坐标系变换到一个新的参考坐标系下，新坐标系的中心点为 $\large C_{\epsilon } = (0.0,-\epsilon )$ ，因此有

$\large P_{\epsilon } = (x_{s},y_{s},z_{s}+\epsilon )$

这里透镜矫正系数 $\large \epsilon$ 的变化范围为0(planar mirrior)到1(parabolic mirror)。

接下来将上式中的点进行归一化，得到归一化平面上的点，

这里先不考虑投影过程中的畸变，最后将归一化的点 $\large \tilde{m}$ 通过相机内参矩阵K投影得到相机成像坐标 $\large \tilde{p}$ 。(s表示坐标轴倾斜系数,如果有知道更多关于s的详细意义的，欢迎补充交流 ~)

$\tilde{p} = \begin{bmatrix} f_{x} & f_{x} s &c_x \\ 0& f_{y} & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_{m}\\ y_{m}\\ 1 \end{bmatrix} = K\tilde{m}$

二、相机畸变模型

2.1、切向径向畸变(RadTan，radial-tangential distortion)

畸变参数[k1,k2,k3,p1,p2]

由于透镜形状引起的畸变成为径向畸变，其畸变程度跟离光心距离有关，使得真实环境中的一条直线在图片中变成曲线，往往越靠近图像的边缘，这种现象越明显。由于实际加工的透镜往往是中心对称的，使得不规则的畸变通畅径向堆成。主要分为桶形畸变和枕形畸变。如果向里弯成为桶形畸变，向外弯称为枕形畸变。如下所示，

另外在相机组装过程中由于不能严格使得透镜和成像平面完全平行，这样引起的畸变称为切向畸变，如下所示，

将归一化平面上一点(x,y)用极坐标系表示(r, $\large \theta$ ),径向畸变是跟r相关的，因此采用有关的二次及高项多项式来进行畸变描述,通畅对于畸变较小的图像中心区域主要是k1起作用，对于畸变较大的边缘区域主要是k2起作用，普通摄像头用这两个系数就可以很好的进行径向畸变的矫正。对于畸变很大的相机，比如鱼眼镜头可以加入k3进行畸变矫正。

$\left\{\begin{matrix} x_{distorted} = x(1+k_{1}r^2 + k_{2}r^4 +k_{3}r^6)\\ \\ y_{distorted} = y(1+k_{1}r^2 + k_{2}r^4 +k_{3}r^6) \end{matrix}\right.$

对于径向畸变可以采用另外两个参数p1和p2表示来进行矫正。

$\left\{\begin{matrix} x_{distorted} = x+2p_{1}xy + p_{2}(r^2+2x^2)\\ \\ y_{distorted} = y + p1(r^2+2y^2) + 2p_{2}xy \end{matrix}\right.$

在同时考虑径向畸变和切向畸变，给定归一化坐标，可以求得原始图像上的坐标

$\left\{\begin{matrix} x_{distorted} = x(1+k_{1}r^2 + k_{2}r^4 +k_{3}r^6) + 2p_{1}xy +p_{2}(r^2+2x^2)\\ \\ y_{distorted} = y(1+k_{1}r^2 + k_{2}r^4 +k_{3}r^6) + p_{1}(r^2+2y^2) + 2p^2xy \end{matrix}\right.$

最后将纠正后的点通过内参投影到像素平面，得到该点图像上的正确位置。

$\left\{\begin{matrix} u= f_{x}x_{distorted} + c_{x}\\ \\ v= f_{y}y_{distorted} + c_{y} \end{matrix}\right.$

2.2视野畸变(FOV,field of view)

畸变参数[ $\omega$ ]，表示FOV畸变参数

$\left\{\begin{matrix} x_{distorted} =\frac{r_{d}}{r}\cdot x\\ \\ y_{distorted} =\frac{r_{d}}{r}\cdot y \end{matrix}\right.$

其中有

$r_{d} =\frac{1}{\omega }arctan(2\cdot r\cdot tan(\frac{\omega }{2}))$ $r = \sqrt{(\frac{X}{Z})^2 +(\frac{Y}{Z})^2 } = \sqrt{x^2 + y^2}$

最后将畸变矫正过的点通过内参矩阵投影就可以得到像素平面坐标上的点。

2.3等距畸变(Equidistant,EQUI)

畸变参数为[k1,k2,k3,k4]

$\left\{\begin{matrix} x_{d} = \frac{\theta _{d}}{r}\cdot x_{c}\\ \\ y_{d} = \frac{\theta _{d}}{r}\cdot y_{c} \end{matrix}\right.$

其中r的含义和 FOV畸变模型中r含义一致， $\theta _{d}$ 的求解如下所示

$\theta = atan2(r, \begin{vmatrix} z_{c} \end{vmatrix}) = atan2(r,1) = atan(r) ,$ $\theta _d = \theta (1 +k_{1}\cdot \theta ^2 + k_{2}\cdot \theta ^4 + k_{3}\cdot \theta ^6 +k_{4}\cdot \theta ^8)$

从下左图可知，当入射光线没有发生折射的时候，即入射角等于出射角，对应图中绿色的线，此时

${r}' = f \cdot tan\theta, x_{d} = f \cdot x_c, y_{d} = f \cdot y_{c}$

但实际中会有产生各种不同的折射，因为这些折射导致出射角小于 $\theta$ ，下图中列举了考虑折射影响四种不同的计算方式，这里谈到的等距畸变就是其中之一，对应图中黑色曲线，其投影在图像平面上得到的点到光轴的距离为：

${r}' = f\cdot \theta$

其距离r'和入射角度 $\theta$ 成正比，因此在右图中关系图中黑色直线是一条曲率为1的直线，我想这也是它被称为等距畸变的原因吧。其他几种的对应关系都是等抛物线形状。

成像点的不同计算方式对比入射角度和曲线变化图

在上面畸变投影中 $\theta_{d}$ 直接和r相比乘以xc就得到畸变后的坐标，属实有点难以理解。不过观察这里根据 $\theta _{d}$ 的形式近似等于 $tan\theta$ 的泰勒展开前五项，

$tan\theta\dot{=}\theta(1+ \frac{1}{3} \theta^2 + \frac{2}{15}\theta^4 + \frac{17}{315}\theta^6 + \frac{62}{2835}\theta^8)$

这里各项都能和上面对应上。因此将 $\theta_{d}$ 替换为 $tan\theta_{d}$ 就可以很好的理解，公式可以重新写为，符合实际的关系。

$\left\{\begin{matrix} \frac{x_{d}}{tan{\theta_{d}}} = \frac{x_c}{r} = \frac{x_{c}}{tan\theta}\\ \\ \frac{y_{d}}{tan{\theta_{d}}} = \frac{y_c}{r} = \frac{y_{c}}{tan\theta} \end{matrix}\right.$

三、特殊的相机名称(MEI, Pinhole,Atan)

采用不同的相机成像模型和畸变模型进行建模描述，会有专门的名字来命名。

MEI Camera: Omni + Radtan

Pinhole Camera: Pinhole + Radtan

Atan Camera: Pinhole + FOV

Davide Scaramuzza Camera:这个是ETHZ Davide Scaramuzza的工作，他将畸变和相机内参放在一起了，为了克服针对鱼眼相机参数模型的知识缺乏，使用一个多项式来代替。

因此当以后我们看到这些相机名字的时候，应该能够反应过来他使用的相机成像模型和畸变模型，以及它们相应的内参形式。另外在相应的视觉SLAM算法中往往涉和支持多种相机模型，在opencv中也有相应的相机模型，如下所示

DSO：Pinhole + Equi / Radtan / FOV

VINS：Pinhole / Omni + Radtan

SVO：Pinhole / atan / Scaramuzza

OpenCV：cv: pinhole + Radtan , cv::fisheye: pinhole + Equi , cv::omnidir: Omni + Radtan

参考文献

[1]各相机模型(针孔+鱼眼)综述_CG-SpatialAI-CSDN博客_plumb_bob

[2]SLAM 中常用的相机模型&畸变模型总结_啊啦啦的博客-CSDN博客_fov模型

[3]相机模型--Omnidirectional Camera_AI小作坊的博客-CSDN博客_omnidirectional

[4]高翔，张涛《视觉SLAM十四讲:从理论到实践》电子工业出版社

[5]Scaramuzza D . Omnidirectional Camera. Springer US, 2014.

[6]Mei C , Rives P . Single View Point Omnidirectional Camera Calibration from Planar Grids[C]// 2007 IEEE International Conference on Robotics and Automation, ICRA 2007, 10-14 April 2007, Roma, Italy. IEEE, 2007.

[7]Kneip L , Scaramuzza D , Siegwart R . A novel parametrization of the perspective-three-point problem for a direct computation of absolute camera position and orientation[C]// The 24th IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2011, Colorado Springs, CO, USA, 20-25 June 2011. IEEE, 2011.

导致格式错误的 Lambda 代理响应的原因以及如何修复它 zqhdz米时空汇编
当人们尝试使用AWSAPIGateway和AWSLambda构建无服务器应用程序时，经常出现的一个问题是_由于配置错误而执行失败：Lambda代理响应格式错误。_没有什么比通用错误消息更糟糕的了，它们不会告诉您解决问题所需的任何内容，对吧？AWS并不是以其错误消息设计而闻名，如果甚至可以这样称呼它的话，更不用说为您提供解决问题的方法了。那么如何修复这个Lambda错误以及是什么原因造成的呢？花椒壳
ROS yaml参数文件的使用 Sun Shiteng ROS
举个例子，若在params.yaml文件中定义如下参数LidarImageFusion:points_src:"/hilbert_h/deskew/cloud_info"image_src:"/usb_cam0/image_raw"camera_info_src:"/home/hdj/fusion_slam/Color_SLAM_ws/src/hilbert_h/config/firefly_8s
xwiki html和css,MediaWiki vs. XWiki Ake阿科多语言信息技术编程数据库操作系统
140Afar,Abkhazian,Afrikaans,Amharic,Arabic,Assamese,Aymara,Azerbaijani,Bashkir,Byelorussian,Bulgarian,Bihari,Bislama,Bengali;Bangla,Tibetan,Breton,Catalan,Corsican,Czech,Welsh,Danish,German,Bhutani,Gr
2021-07-07 潇洒二爷
一辆特斯拉“花格子S型”小车，突然起火，电子技术的车门也失灵TeslaModelSPlaidbrokeintofirewithfailureofelctronicdoors一辆“花格子牌”（ModelSPlaid）特斯拉轿车，在6月29日这天，车主正在路上行驶，突然烈焰腾飞，他的代理律师说，他被短时间困在车内，因为几个电动门都打不开。事情在几天前发生于费城外，这名男子拿到这款特斯拉之后，号称是世界
力扣刷题记录（一）剑指Offer（第二版）乘凉~ 求职过程记录 leetcode 链表算法
1、本栏用来记录社招找工作过程中的内容，包括基础知识学习以及面试问题的记录等，以便于后续个人回顾学习；暂时只有2023年3月份，第一次社招找工作的过程；2、个人经历：研究生期间课题是SLAM在无人机上的应用，有接触SLAM、Linux、ROS、C/C++、DJIOSDK等；3、参加工作后（2021-2023年）岗位是嵌入式软件开发，主要是服务器开发，Linux、C/C++、网络编程、docker容
论文笔记—NDT-Transformer: Large-Scale 3D Point Cloud Localization using the Normal Distribution Transfor 入门打工人笔记 slam 定位算法
论文笔记—NDT-Transformer:Large-Scale3DPointCloudLocalizationusingtheNormalDistributionTransformRepresentation文章摘要~~~~~~~在GPS挑战的环境中，自动驾驶对基于3D点云的地点识别有很高的要求，并且是基于激光雷达的SLAM系统的重要组成部分（即闭环检测）。本文提出了一种名为NDT-Transf
深度学习特征提取魔改版太强了！发文香饽饽！深度之眼深度学习干货人工智能干货人工智能深度学习机器学习论文特征提取
要说CV领域经久不衰的研究热点，特征提取可以占一席，毕竟SLAM、三维重建等重要应用的底层都离不开它。再加上近几年深度学习兴起，用深度学习做特征提取逐渐成了主流，比传统算法无论是性能、准确性还是效率都更胜一筹。目前比较常见的深度学习特征提取方法有基于transformer、基于CNN、基于LSTM以及基于GAN，都发展的比较成熟。但为了追求更快速、准确、鲁棒的特征点提取，研究者们开始致力于改进深度
视觉SLAM十四讲学习笔记——第十讲后端优化（2）晒月光12138 视觉SLAM十四讲学习笔记 slam ubuntu
上文提到考虑全局的后端优化计算量非常大，因此在计算增量方程时，借助H矩阵的稀疏性加速运算。但是随着时间的推移，累积的相机位姿和路标数量还是会导致计算量过大，以上一节的示例代码数据为例：16张图像，共提取到22106个特征点，这些特征点共出现了83718次。对于一个20Hz更新速度，上述的数据量甚至还不到1s的内容，因此在求解大规模定位建图问题时，一定要控制BA的规模。这里主要有两种解决思路：（1）
《Java基础知识》Java Lambda表达式 Limingmingaa java java 开发语言蓝桥杯
接触Lambda表达式的时候，第一感觉就是，这个是啥？我居然看不懂，于是开始寻找资料，必须弄懂它。先来看一个案例：@FunctionalInterfacepublicinterfaceMyLamda{voidtest1(Stringy);}importdemo.knowledgepoints.Lambda.inf.MyLamda;publicclassLambdaTest{publicsta
NDT算法 Joeybee SLAM 算法
上一次我们学习了高翔《自动驾驶与机器人中的SLAM技术》中的三维ICP算法，其中包括点对点、点对线、点对面的ICP算法，本次博客学习NDT算法的源码。NDT算法与ICP算法的最大不同之处，在我看来是NDT考虑了均值和方差这两个局部统计量。从最后的求解方法来看，NDT采用了加权最小二乘问题的高斯-牛顿法，和ICP算法的最明显区别是多了权重分布。从高翔书中的测试结果来看，NDT的收敛速度稍弱于点对面I
SLAM中常用的库 wq_151 人工智能 SLAM 计算机视觉人工智能机器学习 slam
SLAM中常用的库关于库关于库Pangolin是一个用于OpenGL显示/交互以及视频输入的一个轻量级、快速开发库，下面是Pangolin的Github网址：githubEigen是一个高层次的C++库，有效支持线性代数，矩阵和矢量运算，数值分析及其相关的算法。pagenanoflann是一个c++11标准库，用于构建具有不同拓扑（R2，R3（点云），SO(2)和SO(3)（2D和3D旋转组））的
【XR】优化SLAM SDK的稳定性大江东去浪淘尽千古风流人物 xr
优化SLAMSDK的稳定性是确保增强现实(AR)和虚拟现实(VR)应用在各种环境和设备上都能稳定运行的关键。以下是一些主要的优化方法：1.传感器融合优化方法:将多个传感器的数据（如摄像头、加速度计、陀螺仪、磁力计）进行融合，以补偿单一传感器可能存在的误差。优势:提高了环境理解的准确性，减少了由于单一传感器误差导致的抖动和漂移现象。实例:ARKit和ARCore都利用了传感器融合技术来增强稳定性。2
ROS2导航SLAM建图探索鱼香ROS ROS2 机器人 SLAM ROS2 导航 SLAM
大家好，我是昨晚熬夜太多脑壳痛的小鱼。今天带大家一起探索一些ROS2+turtlebot3的slam建图。先上最终效果图1.安装ROS2第一步就是要有一个ROS2的环境，这个没有的请打开小鱼的fishros网站，选择一行代码安装ROS2进行安装。2.安装turtlebot3sudoaptinstallros-foxy-turtlebot3*sudoaptinstallros-foxy-cartog
数百倍加速！港科大最新：嵌入式平台上实时运行的NeRF SLAM！计算机视觉工坊 3D视觉从入门到精通学习自动驾驶算法
来源：计算机视觉工坊添加微信：dddvision，备注：NeRF，拉你入群。文末附行业细分群0.笔者个人体会传统的NeRF和NeRFSLAM所需要的计算量非常大，很难在嵌入式设备上跑起来，这也就很大程度上限制了NeRFSLAM的落地。但最近港科大&中山大学提出了一项工作Photo-SLAM，不仅实现了高保真的建图，还可以在嵌入式设备上实时运行，甚至渲染速度提高了数百倍。下面一起来阅读一下这项工作，
自动驾驶-机器人-slam-定位面经和面试知识系列07之C++STL面试题（03） lonely-stone 面试 c++职场和发展
这个博客系列会分为C++STL-面经、常考公式推导和SLAM面经面试题等三个系列进行更新，基本涵盖了自己秋招历程被问过的面试内容（除了实习和学校项目相关的具体细节）。在知乎和牛客也会同步更新，全网同号（lonely-stone或者lonely_stone）。关于高频面试题和C++STL面经，每次我会更新10个问题左右，每次更新过多，害怕大家可能看了就只记住其中几个点。（在个人秋招面试过程中，面试到
激光SLAM--(8) LeGO-LOAM论文笔记 lonely-stone slam 激光SLAM 论文阅读
论文标题：LeGO-LOAM：LightweightandGround-OptimizedLidarOdometryandMappingonVariableTerrain应用在可变地形场景的轻量级的、并利用地面优化的LOAMABSTRACT轻量级的、基于地面优化的LOAM实时进行六自由度位姿估计，应用在地面的车辆上。强调应用在地面车辆上是因为在这里面要求雷达必须水平安装，而像LOAM和LIO-SA
自动驾驶-机器人-slam-定位面经和面试知识系列03之C++STL面试题（01） lonely-stone 面试 c++职场和发展
这两天有点忙耽搁了，抱歉！！！这个博客系列会分为C++STL-面经、常考公式推导和SLAM面经面试题等三个系列进行更新，基本涵盖了自己秋招历程被问过的面试内容（除了实习和学校项目相关的具体细节）。在知乎和牛客也会同步更新，全网同号（lonely-stone或者lonely_stone）。关于高频面试题和C++STL面经，每次我会更新10个问题左右，每次更新过多，害怕大家可能看了就只记住其中几个点。
自动驾驶-机器人-slam-定位面经和面试知识系列04之高频面试题（02） lonely-stone 自动驾驶机器人面试
这个博客系列会分为C++STL-面经、常考公式推导和SLAM面经面试题等三个系列进行更新，基本涵盖了自己秋招历程被问过的面试内容（除了实习和学校项目相关的具体细节）。在知乎和牛客也会同步更新，全网同号（lonely-stone或者lonely_stone）。关于高频面试题和C++STL面经，每次我会更新10个问题左右，每次更新过多，害怕大家可能看了就只记住其中几个点。（在个人秋招面试过程中，面试到
【自动驾驶】自动驾驶地图构建方法与工具小结 CS_Zero 自动驾驶人工智能
自动驾驶地图构建小结概述制作流程主要利用定位与建图算法（组合导航，视觉、激光SLAM等），融合多种传感器数据，构建高精度、高分辨率的三维语义地图，将要素矢量化，构建要素间的关联关系，通过质检确保质量可靠，形成地图引擎（服务、API）以满足自动驾驶系统的需求。底图构建底图构建存在两大类方法，点云建图与视觉建图。点云建图一般面向高精度采集设备，采用高线束激光雷达，硬件成本高。一般使用高精度组合导航进行
Android D8 编译器和 R8 工具，【一篇文章搞懂】安卓开发top Android android java eclipse 移动开发
android.enableIncrementalDesugaring=false.android.enableDesugar=false2.1Lambda表达式Java8中一个重大变更是引入Lambda表达式。publicclassLambda{publicstaticvoidmain(String[]args){logDebug(msg->System.out.println(msg),"He
特斯拉神器TeslaMate一键安装，终于来了 oakley0 car tesla 云服务器腾讯云
之前分享了teslamate的功能和简单安装方法，很多喜欢尝鲜的车友尝试了，但安装过程对不熟悉linux服务器的非码农来说还是有点小艰辛。趁这回双十一腾讯云重磅优惠，我也重新屯了服务器重装了一遍，现在把简化后安装过程、一键安装方法包括加密登录的方式分享一下。目录1.购买服务器2.登录服务器3.安装TeslaMate3.1切换管理员用户3.2一键安装TeslaMate-【简单模式】3.3一键安装Te
特斯拉神器TeslaMate一键安装，来了 oakley04 腾讯云阿里云云计算
之前分享了teslamate的功能和简单安装方法，很多喜欢尝鲜的车友尝试了，但安装过程对不熟悉linux服务器的非码农来说还是有点小艰辛。趁这回双十一腾讯云重磅优惠，我也重新屯了服务器重装了一遍，现在把简化后安装过程或一键安装方法分享一下。1.购买服务器以下三款服务器都可以，其中最推荐中间的2核4G8M带宽的三年198，还没入手请点击下面的入口链接：腾讯云运营活动-腾讯云https://curl.
TeslaMate特斯拉神器本地Docker部署实现无公网远程访问 nagiY てんさい docker 容器运维 sql
文章目录1.Docker部署TeslaMate2.本地访问TeslaMate3.Linux安装Cpolar4.配置TeslaMate公网地址5.远程访问TeslaMate6.固定TeslaMate公网地址7.固定地址访问TeslaMateTeslaMate是一个开源软件，可以通过连接特斯拉账号，记录行驶历史，统计能耗、里程、充电次数等数据。用户可以通过web界面查看车辆状态、行程报告、充电记录等信
Ubuntu环境搭建TeslaMate，特斯拉车友必备，可视化数据仪表！使用极空间Z4虚拟机喵不是白养的 ubuntu linux
能点进来的大概率都是特斯拉车友~~本篇记录一下使用极空间Z4家庭NAS搭建TeslaMate的全过程，使用极空间最近更新的虚拟机功能，在虚拟机中安装Ubuntu部署Docker。当然大家用PC虚拟机搭建也可以啦！至于为什么不用极空间自带的Docker功能，emmm并不好用。要是想要使用自带的docker来搭建，可以参照这个https://post.smzdm.com/p/az59px95/本人自学
使用Docker部署TeslaMate并结合内网穿透软件实现远程访问车辆数据比奥利奥还傲. docker 容器运维服务器 linux
文章目录1.Docker部署TeslaMate2.本地访问TeslaMate3.Linux安装Cpolar4.配置TeslaMate公网地址5.远程访问TeslaMate6.固定TeslaMate公网地址7.固定地址访问TeslaMateTeslaMate是一个开源软件，可以通过连接特斯拉账号，记录行驶历史，统计能耗、里程、充电次数等数据。用户可以通过web界面查看车辆状态、行程报告、充电记录等信
如何在本地服务器部署TeslaMate并远程查看特斯拉汽车数据无需公网ip 日出等日落内网穿透服务器汽车 tcp/ip
文章目录1.Docker部署TeslaMate2.本地访问TeslaMate3.Linux安装Cpolar4.配置TeslaMate公网地址5.远程访问TeslaMate6.固定TeslaMate公网地址7.固定地址访问TeslaMateTeslaMate是一个开源软件，可以通过连接特斯拉账号，记录行驶历史，统计能耗、里程、充电次数等数据。用户可以通过web界面查看车辆状态、行程报告、充电记录等信
伊朗藏红花前五个月出口增长33% 西域竹君斋
Iran’ssaffronexportsincreased33percentduringthefirstfivemonthsofthecurrentIraniancalendaryear(March21-August22)comparedtothesameperiodoftimeinthepastyear,accordingtothelatestdatareleasedbytheIslamicRe
如何实现基于图像与激光雷达的 3d 场景重建? 大势智慧 3d 人工智能计算机视觉三维建模激光点云
智影S100是一款基于图像和激光点云融合建模技术的高精度轻巧手持SLAM三维激光扫描仪。设备机身小巧、手持轻便，可快速采集点云数据；支持实时解算、实时预览点云成果，大幅提高内外业工作效率；同时支持一键生成实景三维Mesh模型，实现城市建筑、堆体、室内空间等场景的高逼真3d重建。以下是智影S100在国家游泳中心“水立方”进行实地采集的点云与模型成果展示：智影S100：水立方立面点云与模型成果分享，实
ROS目标跟随（路径规划、雷达、slam、定位）海风- ROS 小车跟随目标跟随雷达路径规划定位
ROS目标跟随（路径规划、雷达、地图、定位）最终效果展示一、总体launch文件1、打开已有地图2、组合小车的各个部分2.1惯性矩阵设置2.2小车底盘2.3摄像头2.4雷达2.5为机器人模型添加传动装置以及控制器2.6为机器人模型添加雷达配置2.7为机器人模型添加摄像头配置2.8为机器人模型添加kinect摄像头配置3、定位系统（amcl）4、路径规划（move_base）4.1全局路径规划与本地
ROS小车跟随海风- ROS 小车跟随目标跟随雷达
这篇的目的是方便自己复习总体流程1、gazebo仿真世界2、机器人模型3、slam建图4、定位5、路径规划6、小车跟随7、总体launch文件第一篇博客给出了总体代码：https://blog.csdn.net/m0_71523511/article/details/135610191第二篇博客改善了跟随的效果：https://blog.csdn.net/m0_71523511/article/d
Dom 周华华 JavaScript html
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd"> <html xmlns="http://www.w3.org/1999/xhtml&q
【Spark九十六】RDD API之combineByKey bit1129 spark
1. combineByKey函数的运行机制 RDD提供了很多针对元素类型为(K,V)的API，这些API封装在PairRDDFunctions类中，通过Scala隐式转换使用。这些API实现上是借助于combineByKey实现的。combineByKey函数本身也是RDD开放给Spark开发人员使用的API之一首先看一下combineByKey的方法说明：
msyql设置密码报错：ERROR 1372 (HY000): 解决方法详解 daizj mysql 设置密码
MySql给用户设置权限同时指定访问密码时，会提示如下错误： ERROR 1372 (HY000): Password hash should be a 41-digit hexadecimal number；问题原因：你输入的密码是明文。不允许这么输入。解决办法：用select password('你想输入的密码');查询出你的密码对应的字符串，然后
路漫漫其修远兮吾将上下而求索周凡杨学习思索
王国维在他的《人间词话》中曾经概括了为学的三种境界古今之成大事业、大学问者，罔不经过三种之境界。“昨夜西风凋碧树。独上高楼，望尽天涯路。”此第一境界也。“衣带渐宽终不悔，为伊消得人憔悴。”此第二境界也。“众里寻他千百度，蓦然回首，那人却在灯火阑珊处。”此第三境界也。学习技术，这也是你必须经历的三种境界。第一层境界是说，学习的路是漫漫的，你必须做好充分的思想准备，如果半途而废还不如不要开始。这里，注
Hadoop(二)对话单的操作朱辉辉33 hadoop
Debug： 1、 A = LOAD '/user/hue/task.txt' USING PigStorage(' ') AS (col1,col2,col3); DUMP A; //输出结果前几行示例： (>ggsnPDPRecord(21),,) (-->recordType(0),,) (-->networkInitiation(1),,)
web报表工具FineReport常用函数的用法总结（日期和时间函数）老A不折腾 finereport 报表工具 web开发
web报表工具FineReport常用函数的用法总结（日期和时间函数）说明：凡函数中以日期作为参数因子的，其中日期的形式都必须是yy/mm/dd。而且必须用英文环境下双引号(" ")引用。 DATE DATE(year,month,day):返回一个表示某一特定日期的系列数。 Year:代表年，可为一到四位数。 Month:代表月份。
c++ 宏定义中的##操作符墙头上一根草 C++
#与##在宏定义中的--宏展开 #include <stdio.h> #define f(a,b) a##b #define g(a) #a #define h(a) g(a) int main() { &nbs
分析Spring源代码之，DI的实现 aijuans spring DI 现源代码
(转) 分析Spring源代码之，DI的实现 2012/1/3 by tony 接着上次的讲，以下这个sample [java] view plain copy print
for循环的进化 alxw4616 JavaScript
// for循环的进化 // 菜鸟 for (var i = 0; i < Things.length ; i++) { // Things[i] } // 老鸟 for (var i = 0, len = Things.length; i < len; i++) { // Things[i] } // 大师 for (var i = Things.le
网络编程Socket和ServerSocket简单的使用百合不是茶网络编程基础 IP地址端口
网络编程;TCP/IP协议网络:实现计算机之间的信息共享,数据资源的交换协议:数据交换需要遵守的一种协议,按照约定的数据格式等写出去端口:用于计算机之间的通信每运行一个程序，系统会分配一个编号给该程序，作为和外界交换数据的唯一标识 0~65535 查看被使用的
JDK1.5 生产消费者 bijian1013 java thread 生产消费者 java多线程
ArrayBlockingQueue：一个由数组支持的有界阻塞队列。此队列按 FIFO（先进先出）原则对元素进行排序。队列的头部是在队列中存在时间最长的元素。队列的尾部是在队列中存在时间最短的元素。新元素插入到队列的尾部，队列检索操作则是从队列头部开始获得元素。 ArrayBlockingQueue的常用方法：
JAVA版身份证获取性别、出生日期及年龄 bijian1013 java 性别出生日期年龄
工作中需要根据身份证获取性别、出生日期及年龄，且要还要支持15位长度的身份证号码，网上搜索了一下，经过测试好像多少存在点问题，干脆自已写一个。 CertificateNo.java package com.bijian.study; import java.util.Calendar; import
【Java范型六】范型与枚举 bit1129 java
首先，枚举类型的定义不能带有类型参数，所以，不能把枚举类型定义为范型枚举类，例如下面的枚举类定义是有编译错的 public enum EnumGenerics<T> { //编译错，提示枚举不能带有范型参数 OK, ERROR; public <T> T get(T type) { return null;
【Nginx五】Nginx常用日志格式含义 bit1129 nginx
1. log_format 1.1 log_format指令用于指定日志的格式，格式： log_format name(格式名称) type(格式样式) 1.2 如下是一个常用的Nginx日志格式： log_format main '[$time_local]|$request_time|$status|$body_bytes
Lua 语言 15 分钟快速入门 ronin47 lua 基础
- - 单行注释 - - [[ [多行注释] - - ]] - - - - - - - - - - - 1. 变量 & 控制流 - - - - - - - - - - num = 23 - - 数字都是双精度 str = 'aspythonstring'
java-35.求一个矩阵中最大的二维矩阵 ( 元素和最大 ) bylijinnan java
the idea is from: http://blog.csdn.net/zhanxinhang/article/details/6731134 public class MaxSubMatrix { /**see http://blog.csdn.net/zhanxinhang/article/details/6731134 * Q35 求一个矩阵中最大的二维
mongoDB文档型数据库特点开窍的石头 mongoDB文档型数据库特点
MongoDD: 文档型数据库存储的是Bson文档-->json的二进制特点：内部是执行引擎是js解释器，把文档转成Bson结构，在查询时转换成js对象。 mongoDB传统型数据库对比传统类型数据库：结构化数据，定好了表结构后每一个内容符合表结构的。也就是说每一行每一列的数据都是一样的文档型数据库：不用定好数据结构，
[毕业季节]欢迎广大毕业生加入JAVA程序员的行列 comsci java
一年一度的毕业季来临了。。。。。。。。正在投简历的学弟学妹们。。。如果觉得学校推荐的单位和公司不适合自己的兴趣和专业，可以考虑来我们软件行业，做一名职业程序员。。。软件行业的开发工具中，对初学者最友好的就是JAVA语言了，网络上不仅仅有大量的
PHP操作Excel – PHPExcel 基本用法详解 cuiyadll PHP Excel
导出excel属性设置//Include classrequire_once('Classes/PHPExcel.php');require_once('Classes/PHPExcel/Writer/Excel2007.php');$objPHPExcel = new PHPExcel();//Set properties 设置文件属性$objPHPExcel->getProperties
IBM Webshpere MQ Client User Issue (MCAUSER) darrenzhu IBM jms user MQ MCAUSER
IBM MQ JMS Client去连接远端MQ Server的时候，需要提供User和Password吗？答案是根据情况而定，取决于所定义的Channel里面的属性Message channel agent user identifier (MCAUSER)的设置。 http://stackoverflow.com/questions/20209429/how-mca-user-i
网线的接法 dcj3sjt126com
一、PC连HUB (直连线)A端：（标准568B）：白橙，橙，白绿，蓝，白蓝，绿，白棕，棕。 B端：（标准568B）：白橙，橙，白绿，蓝，白蓝，绿，白棕，棕。二、PC连PC （交叉线）A端：(568A)：白绿，绿，白橙，蓝，白蓝，橙，白棕，棕； B端：（标准568B）：白橙，橙，白绿，蓝，白蓝，绿，白棕，棕。三、HUB连HUB&nb
Vimium插件让键盘党像操作Vim一样操作Chrome dcj3sjt126com chrome vim
什么是键盘党？键盘党是指尽可能将所有电脑操作用键盘来完成，而不去动鼠标的人。鼠标应该说是新手们的最爱，很直观，指哪点哪，很听话！不过常常使用电脑的人，如果一直使用鼠标的话，手会发酸，因为操作鼠标的时候，手臂不是在一个自然的状态，臂肌会处于绷紧状态。而使用键盘则双手是放松状态，只有手指在动。而且尽量少的从鼠标移动到键盘来回操作，也省不少事。在chrome里安装 vimium 插件
MongoDB查询（2）——数组查询[六] eksliang mongodb MongoDB查询数组
MongoDB查询数组转载请出自出处：http://eksliang.iteye.com/blog/2177292 一、概述 MongoDB查询数组与查询标量值是一样的，例如，有一个水果列表，如下所示： > db.food.find() { "_id" : "001", "fruits" : [ "苹
cordova读写文件（1） gundumw100 JavaScript Cordova
使用cordova可以很方便的在手机sdcard中读写文件。首先需要安装cordova插件：file 命令为： cordova plugin add org.apache.cordova.file 然后就可以读写文件了，这里我先是写入一个文件，具体的JS代码为： var datas=null;//datas need write var directory=&
HTML5 FormData 进行文件jquery ajax 上传到又拍云 ileson jquery Ajax html5 FormData
html5 新东西：FormData 可以提交二进制数据。页面test.html <!DOCTYPE> <html> <head> <title> formdata file jquery ajax upload</title> </head> <body> <
swift appearanceWhenContainedIn:(version1.2 xcode6.4) 啸笑天 version
swift1.2中没有oc中对应的方法： + (instancetype)appearanceWhenContainedIn:(Class <UIAppearanceContainer>)ContainerClass, ... NS_REQUIRES_NIL_TERMINATION; 解决方法：在swift项目中新建oc类如下： #import &
java实现SMTP邮件服务器 macroli java 编程
电子邮件传递可以由多种协议来实现。目前，在Internet 网上最流行的三种电子邮件协议是SMTP、POP3 和 IMAP，下面分别简单介绍。　　◆ SMTP 协议　　简单邮件传输协议(Simple Mail Transfer Protocol,SMTP)是一个运行在TCP/IP之上的协议，用它发送和接收电子邮件。SMTP 服务器在默认端口25上监听。SMTP客户使用一组简单的、基于文本的
mongodb group by having where 查询sql qiaolevip 每天进步一点点学习永无止境 mongo 纵观千象
SELECT cust_id, SUM(price) as total FROM orders WHERE status = 'A' GROUP BY cust_id HAVING total > 250 db.orders.aggregate( [ { $match: { status: 'A' } }, { $group: {
Struts2 Pojo（六） Luob. POJO strust2
注意：附件中有完整案例 1.采用POJO对象的方法进行赋值和传值 2.web配置 <?xml version="1.0" encoding="UTF-8"?> <web-app version="2.5" xmlns="http://java.sun.com/xml/ns/javaee&q
struts2步骤 wuai struts
1、添加jar包 2、在web.xml中配置过滤器 <filter> <filter-name>struts2</filter-name> <filter-class>org.apache.st

相机的成像模型(Pinhole + Omni)和畸变模型(RanTan, FOV, EQUI)

总述

一、相机成像模型

1.1 针孔模型，参数[fx, fy, cx, cy]

1.2全向模型，参数[, fx, fy, cx, cy]

二、相机畸变模型

2.1、切向径向畸变(RadTan，radial-tangential distortion)

2.2视野畸变(FOV,field of view)

2.3等距畸变(Equidistant,EQUI)

三、特殊的相机名称(MEI, Pinhole,Atan)

参考文献

你可能感兴趣的:(slam)

1.2全向模型，参数[ $\epsilon$ , fx, fy, cx, cy]