【AM】Glow-TTS: A Generative Flow for Text-to-Speech via Monotonic Alignment Search
文章目录
-
-
- 1. Related Work
-
- 1.1. Alignment Estimation between Text and Speech
- 1.2. Text-to-Speech Models
- 1.3. Flow-based Generative Models
- 2. GLOW-TTS
-
- 2.1. Training and Inference Procedures
- 2.2. Monotonic Alignment Search
-
Glow-TTS: A Generative Flow for Text-to-Speech via Monotonic Alignment Search
来源:NeurIPS 2020
单位:Kakao Enterprise
最近TTS的模型如fastspeech或ParaNet,都是以并行方式产生mel谱。尽管可以并行,但是这些模型在训练时需要一个额外的TTS模型产生对齐(或者采用识别的强制对齐)。本文利用了flow和动态规划,提出了Glow-TTS, 能够自己产生文本和mel谱之间的单调的对齐,不需要借助额外的模型产生对齐。本文采用的强制单调对齐的方法增强了TTS的鲁棒性,由于是基于flow的方法提升了合成的速度。与自回归的模型Tacotron2相比,Glow-TTS实现了一个数量级的加速,并且合成效果与Tacotron2相当。
开源代码链接:glow-tts
1. Related Work
1.1. Alignment Estimation between Text and Speech
首先是文本和语音的对齐问题。传统的方法通过HMM估计文本和语音的对齐。在语音识别中,也可以通过CTC得到文本和语音之间的对齐。这两种方法都可以通过前向后向算法(用到了动态规划)得到文本和语音之间的对齐。本文也引入了一个相似的动态规划的方法得到文本域语音之间的对齐,与CTC不同的是本文的对齐方法是生成性的方法(CTC是区分性的),与HMM不同的是,本文的方法可以并行地对序列采样,并且没有观察之间的条件独立假设。
1.2. Text-to-Speech Models
最近,一些工作尝试并行地生成MEL谱,如Fastspeech、ParaNet,显著地加速了自回归的TTS模型。然而这些并行化的TTS model都需要用事先训好的自回归模型提取语音和文本之间的对齐。本文的方法不需要这样一个额外模型去做预对齐。
1.3. Flow-based Generative Models
Flow-based Generative Model是生成模型的一种flow-based geneative model。和本文工作同期的TTS模型还有AlignTTS, Flowtron , and Flow-TTS,其中AlignTTS和Flow-TTS不需要额外的对齐模型,Flowtron是一个flow based的模型,AlignTTS不是Flow-based模型(是基于Transformer encoder的结构,也可以并行产生MEL谱,不需要自回归的过程),Flowtron和FlowTTS使用了soft attention(不能保证单调性),本文提出的方法既利用了hard monotonic alignment有利用了generativate flow,分别结合了二者在鲁棒性和可控性的优势。
2. GLOW-TTS
2.1. Training and Inference Procedures
x x x表示MEL谱, c c c表示文本序列,Glow-TTS对 P X ( x ∣ c ) P_{X}(x \mid c) PX(x∣c)建模,首先将条件先验分布 P Z ( z ∣ c ) P_{Z}(z \mid c) PZ(z∣c)通过flow-based的decoder建模 f dec : z → x f_{\text {dec}}: z \rightarrow x fdec:z→x,可以计算Glow-based的生成模型的log-likelihood为:
E q u a t i o n 1 : log P X ( x ∣ c ) = log P Z ( z ∣ c ) + log ∣ det ∂ f d e c − 1 ( x ) ∂ x ∣ Equation\ 1:\log P_{X}(x \mid c)=\log P_{Z}(z \mid c)+\log \left|\operatorname{det} \frac{\partial f_{d e c}^{-1}(x)}{\partial x}\right| Equation 1:logPX(x∣c)=logPZ(z∣c)+log∣∣∣∣det∂x∂fdec−1(x)∣∣∣∣
右项是一个与模型参数相关的量,现在看左项。
假设网络的分布由参数 θ \theta θ刻画,对齐函数 A \textbf{A} A, P Z P_{Z} PZ是isotropic multivariate Gaussian distribution,刻画分布的 μ \mu μ and σ \sigma σ由encoder f enc f_{\text {enc}} fenc得到。Encoder将text c = c 1 : T t e x t c=c_{1: T_{t e x t}} c=c1:Ttext映射到统计量 μ = μ 1 : T text \mu=\mu_{1: T_{\text {text}}} μ=μ1:Ttext, σ = σ 1 : T text \sigma=\sigma_{1: T_{\text {text}}} σ=σ1:Ttext, T text T_{\text {text}} Ttext表示文本的长度。对齐矩阵 A \textbf{A} A中的元素 A ( j ) = i A(j)=i A(j)=i if z j ∼ N ( z j ; μ i , σ i ) z_{j} \sim N\left(z_{j} ; \mu_{i}, \sigma_{i}\right) zj∼N(zj;μi,σi),表示第 j j j帧MEL谱对齐到了第 i i i个文本上。那么左项还可以写为:
E q u a t i o n 2 : log P Z ( z ∣ c ; θ , A ) = ∑ j = 1 T m e l log N ( z j ; μ A ( j ) , σ A ( j ) ) Equation\ 2:\log P_{Z}(z \mid c ; \theta, A)=\sum_{j=1}^{T_{m e l}} \log \mathcal{N}\left(z_{j} ; \mu_{A(j)}, \sigma_{A(j)}\right) Equation 2:logPZ(z∣c;θ,A)=j=1∑TmellogN(zj;μA(j),σA(j))
T m e l T_{m e l} Tmel表示MEL谱的长度。我们的学习目标是找到参数 θ \theta θ和对齐 A \textbf{A} A, 使得log-likelihood最大。将这个复杂的问题分成两步:1)根据现有的参数 θ \theta θ搜索最可能的单调的对齐 A ∗ A^{*} A∗,如下公式4。2)通过最大化 log p X ( x ∣ c ; θ , A ∗ ) \log p_{X}\left(x \mid c ; \theta, A^{*}\right) logpX(x∣c;θ,A∗)更新参数 θ \theta θ,如下公式3,这两个步骤迭代进行(本质上是一个EM过程)。在每个训练步,首先推断出 A ∗ A^{*} A∗,然后通过梯度下降法更新 θ \theta θ。计算对齐的过程中,采用了Viterbi算法,找到最可能的对齐的最大log-likelihood。这样的过程虽然不能保证得到下式的全局最优解,但是可以不断优化log-likelihood的下界。
E q u a t i o n 3 : max θ , A L ( θ , A ) = max θ , A log P X ( x ∣ c ; A , θ ) Equation\ 3:\max _{\theta, A} L(\theta, A)=\max _{\theta, A} \log P_{X}(x \mid c ; A, \theta) Equation 3:θ,AmaxL(θ,A)=θ,AmaxlogPX(x∣c;A,θ)
E q u a t i o n 4 : A ∗ = arg max A log P X ( x ∣ c ; A , θ ) = arg max A ∑ j = 1 T mel log N ( z j ; μ A ( j ) , σ A ( j ) ) Equation\ 4:A^{*}=\underset{A}{\arg \max } \log P_{X}(x \mid c ; A, \theta)=\underset{A}{\arg \max } \sum_{j=1}^{T_{\text {mel}}} \log \mathcal{N}\left(z_{j} ; \mu_{A(j)}, \sigma_{A(j)}\right) Equation 4:A∗=AargmaxlogPX(x∣c;A,θ)=Aargmaxj=1∑TmellogN(zj;μA(j),σA(j))
在inference阶段,也同fastspeech一样引入了一个Duration预测模型,这个Duration预测模型接在encoder的顶层,训练时采用MSE loss,为了防止Duration预测的梯度影响log likelihood的计算,禁止Duartion预测部分的梯度传到encoder,如公式5、6所示。
E q u a t i o n 5 : d i = ∑ j = 1 T m e l 1 A ∗ ( j ) = i , i = 1 , … , T t e x t Equation\ 5:d_{i}=\sum_{j=1}^{T_{m e l}} 1_{A^{*}(j)=i}, i=1, \ldots, T_{t e x t} Equation 5:di=j=1∑Tmel1A∗(j)=i,i=1,…,Ttext
E q u a t i o n 6 : L d u r = M S E ( f d u r ( s g [ f e n c ( c ) ] ) , d ) Equation\ 6:L_{d u r}=M S E\left(f_{d u r}\left(s g\left[f_{e n c}(c)\right]\right), d\right) Equation 6:Ldur=MSE(fdur(sg[fenc(c)]),d)
其训练过程的流程图如下图所示,现根据目前网络的参数估计一个 A ∗ A^* A∗,根据这个 A ∗ A^* A∗得到 z \textbf{z} z,并得到decoder 的输出,根据 Log-likelihood最大原则,更新decoder部分的参数,并更新了 z \textbf{z} z,反推A*,更新 μ \mu μ, σ \sigma σ,从而梯度可以传到encoder部分。
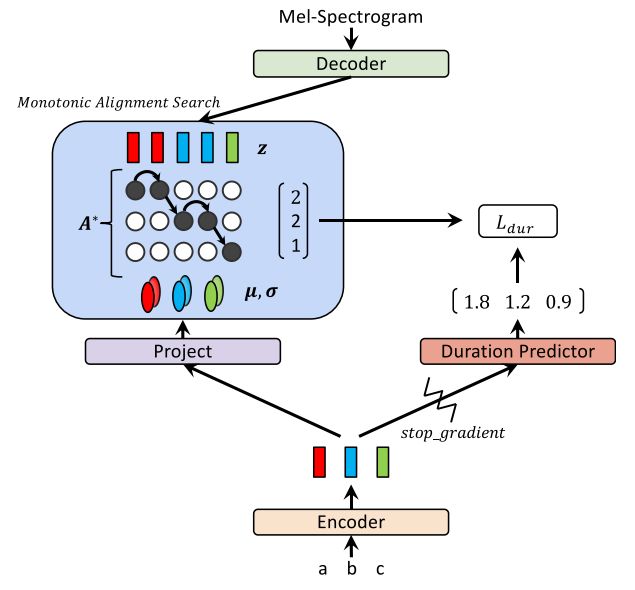
其 inference 时的流程图,如下图所示,通过 Duration 模块对时长的预测,将 encoder 的输出进行扩展,扩展为 z \textbf{z} z,然后通过 glow-based 生成模型,生成 MEL 谱。
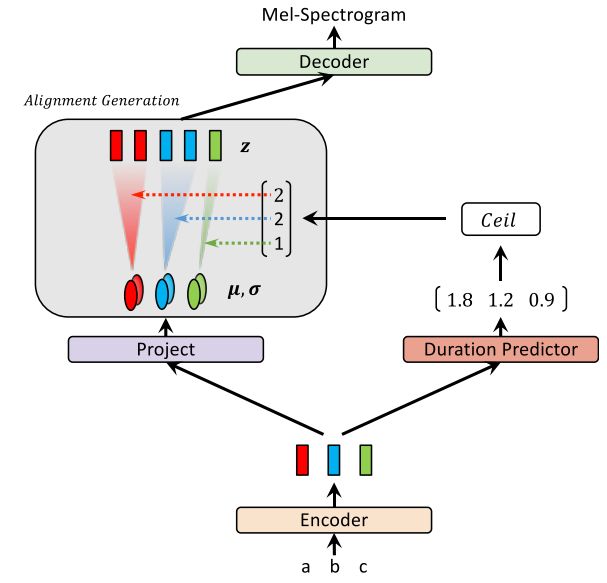
2.2. Monotonic Alignment Search
单向的对齐如图所示,即隐式表达 z j z_j zj对齐文本 c i c_i ci,那么 z j + 1 z_{j+1} zj+1只能对齐到 c i c_i ci或者 c i + 1 c_{i+1} ci+1(不会对齐到 < i − 1
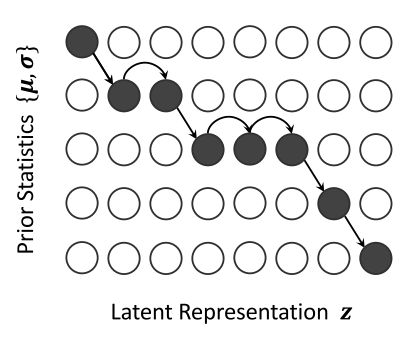
那么单向的对齐 A ∗ \textbf{A}^* A∗如何计算呢?这里借助了 Q \textbf{Q} Q矩阵。 Q i j Q_{ij} Qij表示隐式表达 z j z_j zj对齐文本 c i c_i ci的最大似然概率。由于其单调性和不允许skip的特性, Q i j Q_ij Qij可以通过其 Q i − 1 , j − 1 Q_{i-1,j-1} Qi−1,j−1、 Q i , j − 1 Q_{i,j-1} Qi,j−1以及 z j z_j zj, { μ i − 1 , σ i − 1 } \left\{\mu_{i-1}, \sigma_{i-1}\right\} {μi−1,σi−1}计算得到。计算过程如公示7所示。
E q u a t i o n 7 : Q i , j = max A ∑ k = 1 j log N ( z k ; μ A ( k ) , σ A ( k ) ) = max ( Q i − 1 , j − 1 , Q i , j − 1 ) + log N ( z j ; μ i , σ i ) Equation\ 7:Q_{i, j}=\max _{A} \sum_{k=1}^{j} \log \mathcal{N}\left(z_{k} ; \mu_{A(k)}, \sigma_{A(k)}\right)=\max \left(Q_{i-1, j-1}, Q_{i, j-1}\right)+\log \mathcal{N}\left(z_{j} ; \mu_{i}, \sigma_{i}\right) Equation 7:Qi,j=Amaxk=1∑jlogN(zk;μA(k),σA(k))=max(Qi−1,j−1,Qi,j−1)+logN(zj;μi,σi)
Q \textbf{Q} Q矩阵计算过程就是一个动态规划的过程,如下图所示。
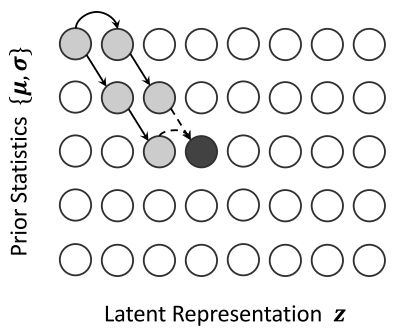
计算完 Q \textbf{Q} Q之后,回溯得到最大Log-likelihood的路径,即得到对齐 A ∗ \textbf{A}^* A∗。