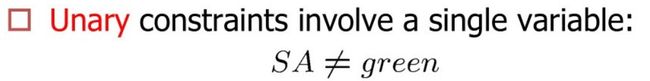人工智能：一种现代方法学习笔记（第六章）——约束满足问题
定义
每一次赋值都会影响下一次的选择范围
约束满足问题指的是针对给定的一组变量及其需要满足的一些限制或一些约束条件，找出符合这些满足这些约束关系的一个解、全部解或是最优解。
CSP可分为两个子领域也就是 表示（Representation）与推理（Reasoning）。表示可分为通用的及应用特点的方法；推理分为搜索与推断。
推断方法，指的是基于约束传播 (Constraint Propagation) 的一种特殊推理方法——在推理过程中，使用约束来减少一个变量的合法取值范围，并将这种影响通过 CSP 网络施加给与之存在约束关系的变量上。
而搜索指的是，从变量的所有可能取值中，选取服从约束的取值。
约束传播与搜索可以交替进行，或者，也可以将约束传播作为搜索前的预处理步骤，此时，约束传播可以消除不满足约束的子空间（压缩）。在搜索过程中，使用约束传播，可以避免对不满足约束的子空间或子树进行搜索，从而大大提高了搜索效率。
约束传播（constraint propagation）VS 局部搜索
约束传播：
- partial assignment(部分赋值)
- 初始状态赋空值
- 在剩余的没有被选择的变量选一个进行操作给其赋值，操作满足对应约束条件
局部搜素：
- full assignment( 一次性将所有变量全部赋值)
- 每次选择一个变量修改值
CSP问题形式化
csp形式化实例
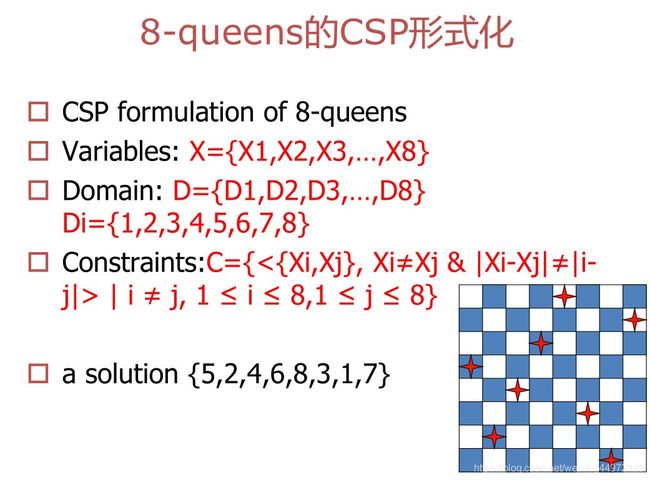
八皇后问题
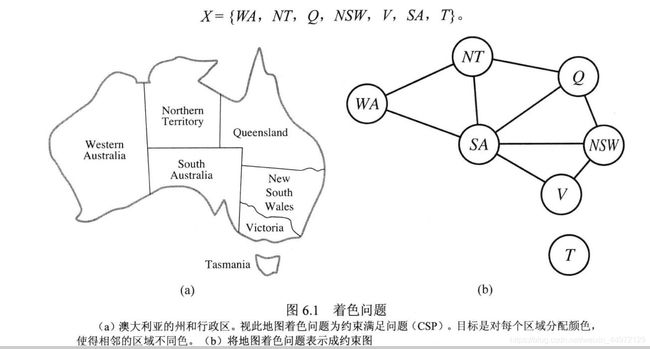
地图着色问题
那个定义域里 WA,NT之类的是他那个地名代表的缩写
约束的类型
绝对约束
- 一元约束：只限制单个变量的取指
- 二元约束：限制多个变量的取指
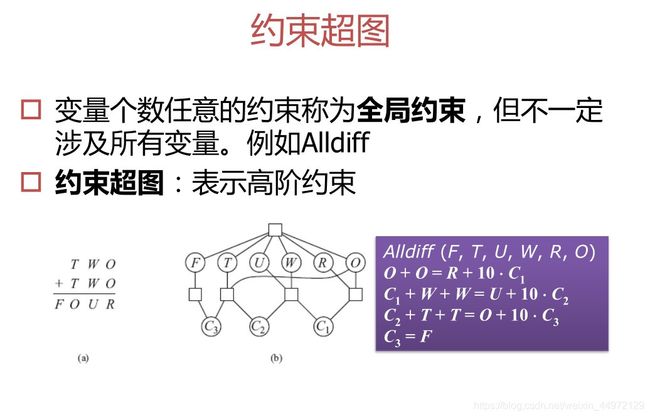
- 高阶约束（也叫作全局约束）：多个变量的约束（n≥2）
偏好约束（约束优化问题，COP）
定理：任何有限值域的约束都可以通过加入条件转化为二元约束
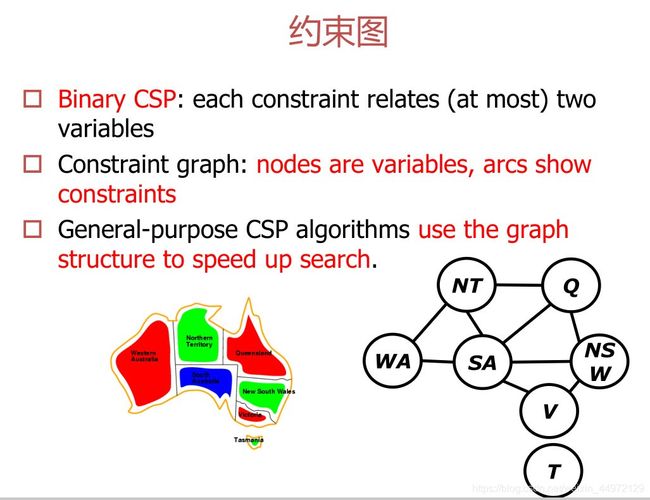
约束图和约束超图
约束传播
概念
约束传播的基本思想是，将一个 CSP 转换为等价的、更简单且易于求解的CSP。其主要技术手段是，消去变量中无效冗余的取值，并将这种变化通过约束变量进行传播，从而也消去那些变量中的无效冗余取值。约束传播可以在不同的粒度上执行，从而形成了不同的约束传播方法。
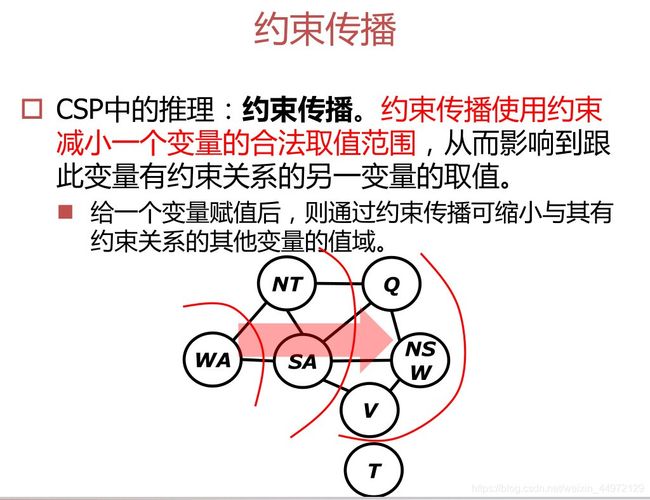
当对问题中变量的赋值满足所有约束时，该赋值是相容的
结点相容
上图例子中的那个约束条件：
弧相容
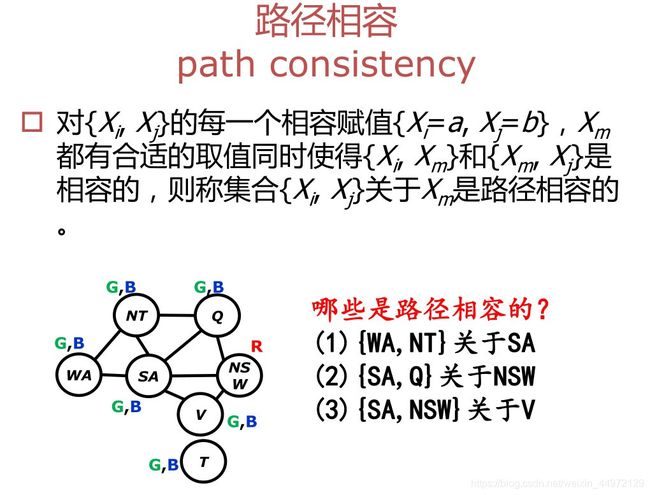
路径相容
K相容
全局约束相容性检查
CSP回溯搜索
形式化一个标准搜索
初始状态：空赋值
转移模型： 选择一个变量赋值
目标测试： 所有变量是否都约束满足条件
路径代价
行动
回溯搜索
提高回溯搜素的效率
变量次序
-
最少剩余值变量优先
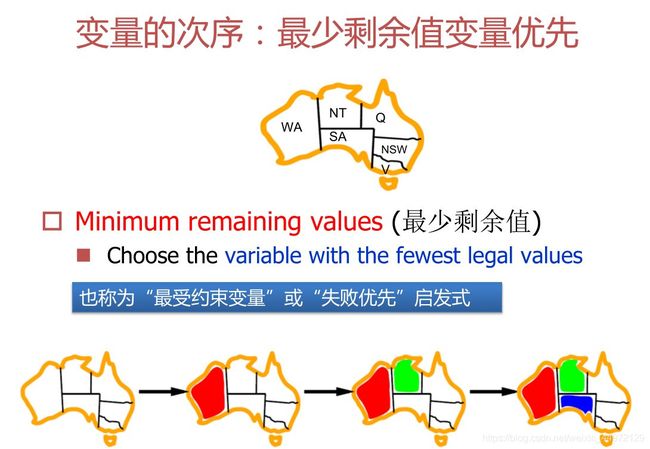
选择那个可以符合约束条件赋值的数量最少的那个变量来进行赋值
但是，如果几个变量有相同的赋值数量剩余值，那么就选择会影响其他变量数最多的那个变量进行赋值（即：最大度变量优先），这样可以有效的减少之后的分支因子 -
最大度变量优先
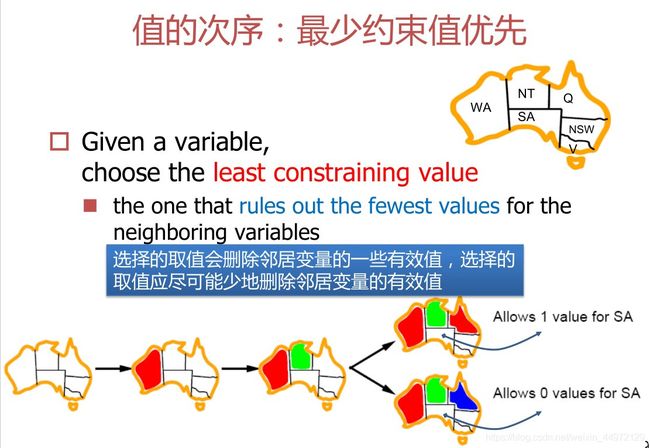
值的次序
变量优先选择哪一个值（推理），从选择值的角度来看，要尽可能的使得剩余变量他们可以选择的值最多（即：最少约束值优先）
推理算法
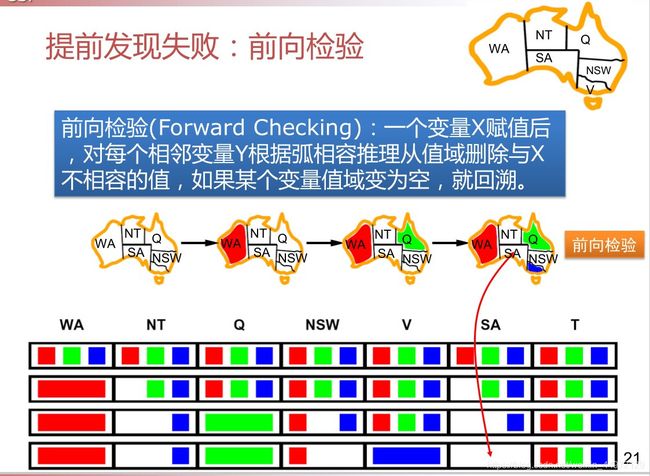
提前发现失败：前向检验
比如上图：第四步的时候，SA可以选择的值域变为空，进行回溯
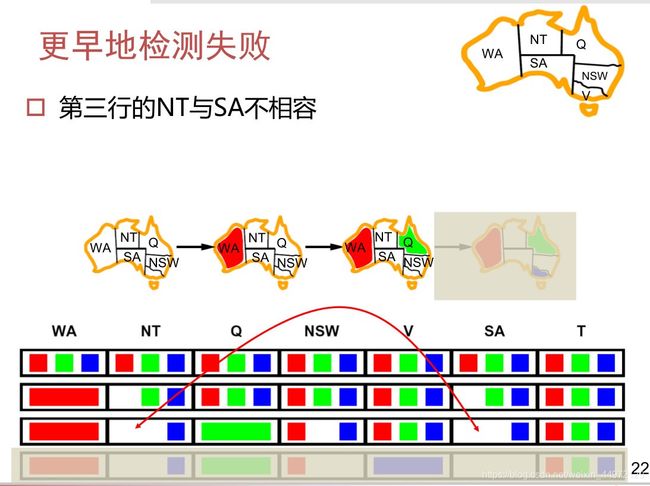
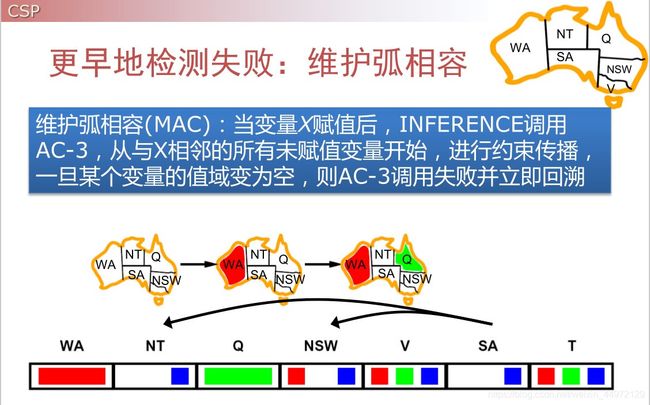
更早的发现失败：维护弧相容
CSP局部搜索
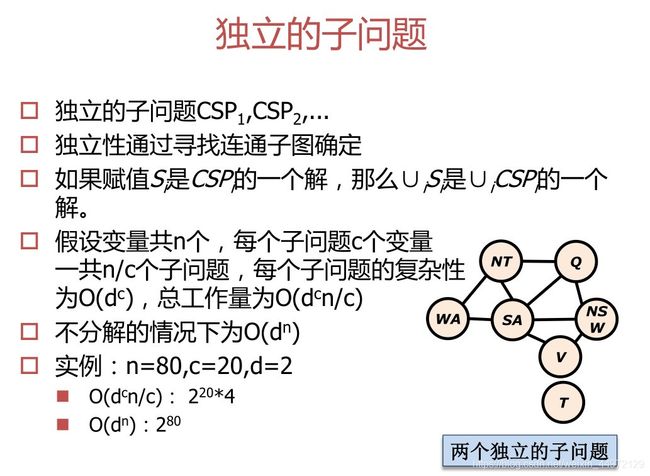
CSP的问题结构
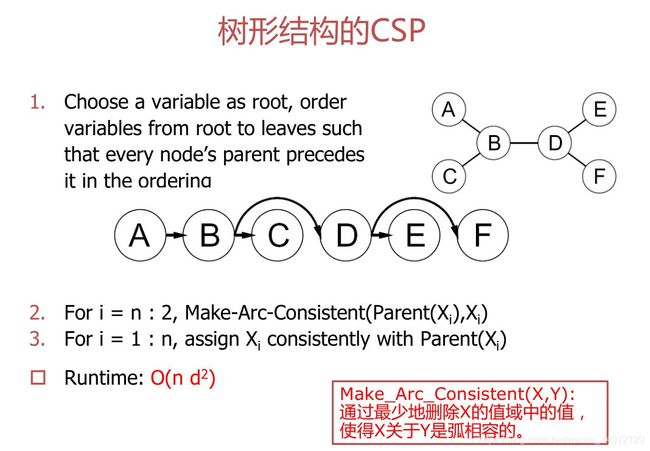
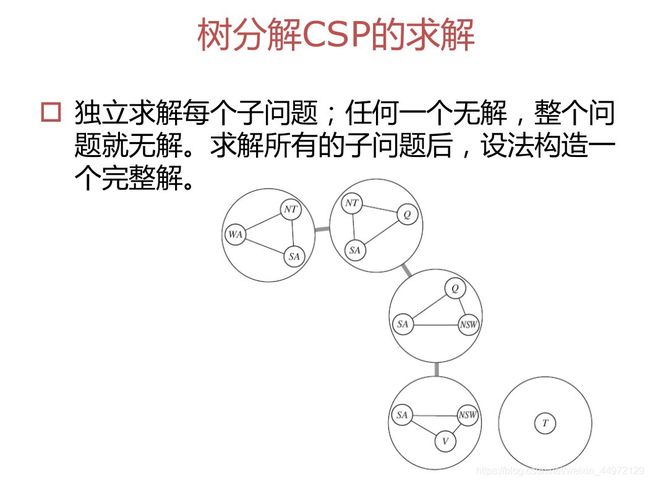
树形结构的CSP
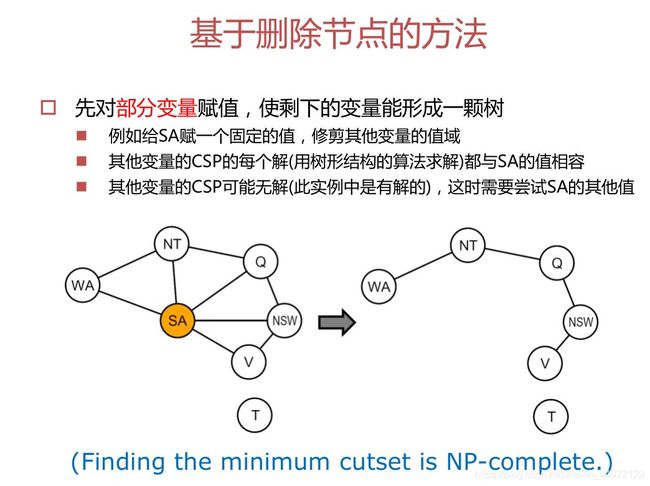
构造树形结构：基于删除结点的办法
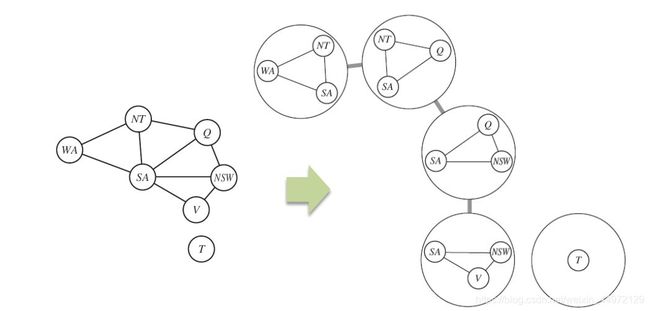
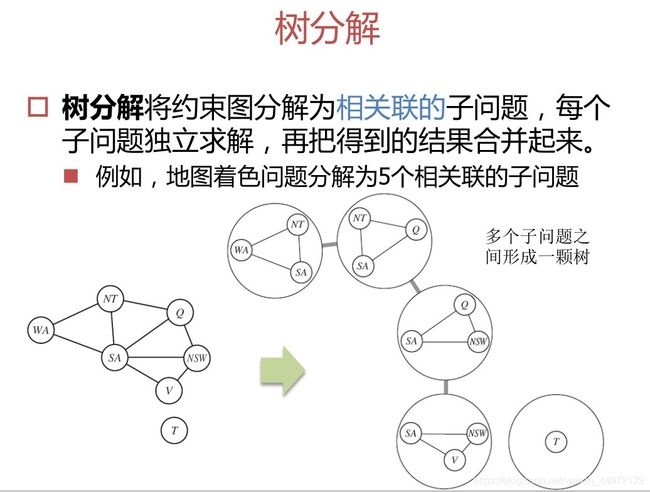
构造树形结构：基于合并结点办法
总结
约束满足问题：
环境：单agent、延续、静态、完全可观察
一种特殊的搜索问题
约束满足问题 vs. 经典搜索问题：
状态s：一组变量(彼此之间有约束)的部分或全部赋值{x1,x2,…,xn}
动作：给每个变量赋不同的值 assignment(xi,v)
状态转移：Result(s, assignment(xi, v))=s’, s’中xi=v, 其它变量赋值与s一致
目标：所有变量都被赋值，且满足约束
当对问题中变量的赋值满足所有约束时，该赋值是相容的
CSP问题的解是所有变量的相容的、完整的赋值
约束满足问题的特性
可交换性 : 对变量赋值的顺序不影响最终结果
约束传播：一个变量的赋值将改变其它变量的值域
约束满足问题的描述
需要描述状态、后继函数、目标测试
最重要的是描述约束
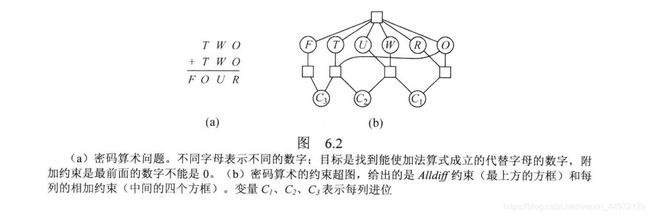
任何CSP都可以转变为只含二元约束的CSP
高阶约束变为二元约束：引进新变量表示变量对的值，引进约束如“X是Y中第一个元素”
改变变量值域消除一元约束
标准搜索过程：
状态为到目前为止的赋值
初始状态: 空赋值, { }
后继函数: 对一个未赋值的变量赋一个可能值
目标检测: 完整的满足所有约束的赋值
与经典搜索的不同之处
Idea 1: 一次只考虑一个变量
Idea 2: 扩展节点时，只考虑当前变量的合法赋值
考虑以上两点的深度优先搜索称为回溯搜索
约束满足问题如何求解
CSP的关键特性: 可交换性和约束传播
下一次选择哪个变量来赋值?
选择值域最小的约束变元
策略1：最小剩余值(Minimum remaining values,MRV)
试图缩小分支因子
策略2：度启发式
选择最受约束的变量先赋值
减少后续变量的分支
在变量的值域中尝试的顺序是什么?
最少约束值（Least constraining value）
选择当前变量的所有可能值中对未赋值变量的值域约束最小的值
我们能否早些检测到失败?
向前检测
跟踪未赋值变量值域变化
当某个变量值域为空时，算法结束
弧相容
X —> Y 是相容的 当且仅当 x的每一个取值y都有可选的值
可以在每次赋值之前做一次弧相容检测
弧相容能够比前向检查更早地检测到失败