（深度学习快速入门）第三章第三节3：深度学习必备组件之优化器和优化算法
文章目录
- 一：优化算法
-
- （1）优化算法概述
- （2）梯度下降法
- 二：优化器
一：优化算法
（1）优化算法概述
优化算法：对于深度学习问题，我们通常会先定义损失函数。一旦我们有了损失函数，我们就可以使用优化算法来尝试最小化损失。在优化中，损失函数通常被称为优化问题的目标函数。优化算法对于深度学习⾮常重要。一方面，训练复杂的深度学习模型可能需要数小时、几天甚至数周。优化算法的性能直接影响模型的训练效率。另一方面，了解不同优化算法的原则及其超参数的作用将使我们能够以有针对性的方式调整超参数，以提高深度学习模型的性能。深度学习中，常见的优化算法有
- 梯度下降算法
- 指数加权平均算法
- 动量梯度下降
- RMSprop算法
- Adam优化算法
这里我们以梯度下降为例介绍一下其优化算法思想。更多关于优化算法的内容详见专栏最优化理论与方法
（2）梯度下降法
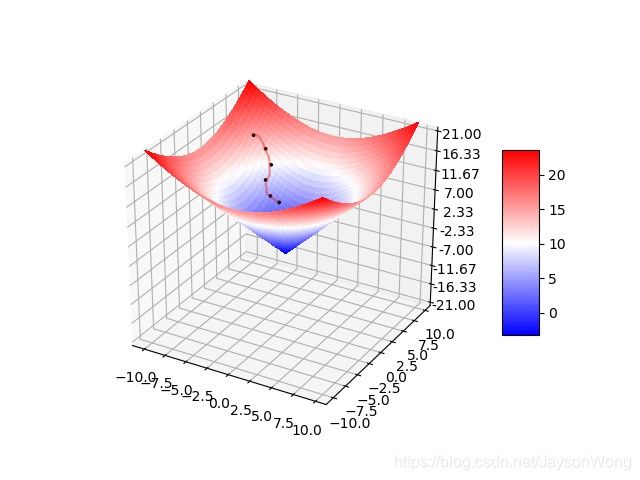
梯度下降法（Gradient descent，GD）：使用梯度下降法寻找函数极小值时，会沿着当前点对应梯度（或近似梯度）的反方向 d d d所规定的步长 α \alpha α内进行迭代搜索。当然如果沿着梯度正方向搜索，就会接近函数的局部最大值，此时对应梯度上升法
我们经常会用下山这个例子来理解梯度下降法：现在你可以想象自己站在一座高山上的某一位置，需要下山，那么此时最快的下山策略就是环顾四周、哪里最陡峭就沿着哪个方向下山，每到一个新的地方后再次执行这个策略
- 在机器学习中，上面的初始位置就相当于损失函数的初始值，山体的陡峭程度则是梯度，对应于损失函数的导数后偏导数
可以看出梯度下降有时得到的是局部最优解，如果损失函数是凸函数，梯度下降法得到的解就是全局最优解
因此，梯度下降法公式为
θ i = θ i − α ∂ J ( θ 0 , θ 1 , … , θ n ) ∂ θ i \theta_{i} = \theta_{i} - \alpha \frac{ \partial J(\theta_{0},\theta_{1},\dots,\theta_{n}) }{ \partial \theta_{i} } θi=θi−α∂θi∂J(θ0,θ1,…,θn)
具体在使用时，我们会使用其变种版本，即小批量梯度下降算法：小批量梯度下降算法是FGD和SGD的折中方案，在一定程度上兼顾了以上两种方法的优点。每次从训练样本集上随机抽取一个小样本集，在抽出来的小样本集上采用FGD迭代更新权重。被抽出的小样本集所含样本点的个数称为batch_size，通常设置为2的幂次方，更有利于GPU加速处理
batch_size=1，则变成了SGDbatch_size=n，则变成了FGD
θ = θ − η ⋅ ∇ θ J ( θ ; x ( i : i + n ) ; y i : i + n ) \theta = \theta - \eta \cdot \nabla_{\theta}J(\theta;x^{(i:i +n)};y^{i: i+n}) θ=θ−η⋅∇θJ(θ;x(i:i+n);yi:i+n)
二：优化器
具体见：PyTorch学习之 torch.optim 的6种优化器及优化算法介绍
Pytorch中优化器主要分为如下两类
- 随机梯度下降系列：SGD、SGD+Momentum；适用于稠密数据
- 自适应学习率系列：AdaGrad、RMSProp、Adam；适用于稀疏数据
好的优化器主要就在于要加快收敛且抑制震荡
