论文笔记 On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima

准奏。

On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima

https://arxiv.org/abs/1609.04836

Overview of the paper

Large batch: worse generalization

Large-batch training makes better use of parallel computing. However, in practice, large-batch training has worse generalization, namely higher error on test dataset. This paper conducts experiments to provide some numerical evidence for the reason why LB works worse than SB.

1. Main observation

• Large-batch methods tend to converge to sharp minimizers
• Small-batch methods converge to flat minimizers

Sharp minimizers are characterized by a significant number of large positive eigenvalues in ${\nabla }^{2}f(x)$, and flat minimizers are characterized by numerous small eigenvalues of ${\nabla }^{2}f(x)$.

The minimum description length theory(MDL) explains how generalization ability is negatively impacted by the training function at a sharp minimizer.

Therefore, the observation gives the reason why large batch methods have worse generalization.

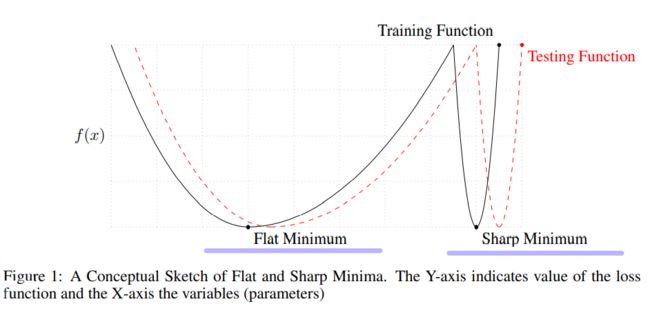
2. Experiments

• Network configurations

Experiments are conducted on different types of networks. Architectures include Alexnet
and VGG.

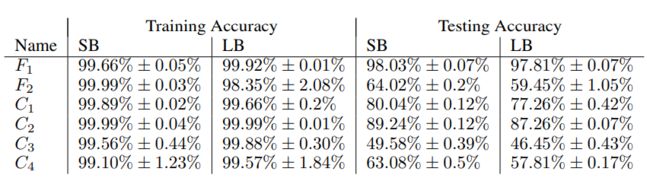
• Performance of LB and SB

In experiment,

• small batch(SB) size : 256 data points
• large batch(LB) size: 10% the size of the dataset

Obviously, the result shows that testing accuracy decreases under large batch methods, though training accuracy increases.

Parametric Plot of $f(\alpha x_l^{\ast }+(1-\alpha )x_s^{\ast })$. Here $f$ is the cross entropy loss.

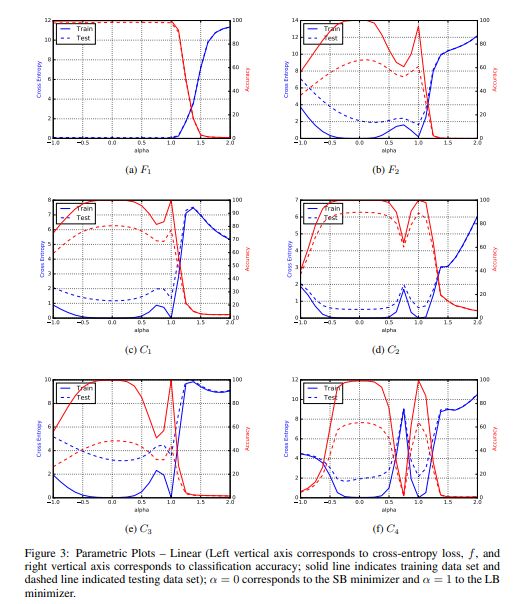
• Sharpness of Minima

1. Sharpness of Minima Measurement

Sharpness of minima can be characterized with the magnitude of the eigenvalues of ${\nabla }^{2}f(x)$, while this measurement has high computation cost.

2. Develop Computationally Feasible Measurement

This paper develops a computationally feasible measure which

• explores a small neighborhood of a solution
• compute the largest value that the function f can attain in the neighborhood

3. Sharpness Computation Detail

To ensure invariance of sharpness to problem dimension and sparsity, define the constraint set ${\mathcal{C}}_{ϵ}$:

The definition of sharpness of $f$ at $x$:

3. Success of Small Batch Methods

A Threshold in Batch Size

In practice, it is often observed that when increasing the batch size, there exists a threshold after which there is a deterioration in testing accuracy.

Why Small batch methods Work Well

• the noise in the gradient pushes the iterates out of the basin of attraction of sharp minimiziers
• encourages movement towards a flatter minimizer

4. Conclusion

The numerical evidence provides support for the following two causes of why LB works worse than SB in generalization.

• LB methods lack the explorative properties of SB methods and tend to zoom-in on the minimizer closest to the initial point.
• SB and LB converge to qualitatively different minimizers with differing generalization properties.

---

Reference:

Keskar, Nitish Shirish, et al. “On large-batch training for deep learning: Generalization gap and sharp minima.” arXiv preprint arXiv:1609.04836 (2016).