狄立克雷函数傅立叶变换0点_【完全吃透】征服傅里叶变换
如果你对信号处理感兴趣,说一天征服傅里叶有点夸张。当然,没有反覆实践和钻研数学, 您无法在一天里学会傅立叶变换的方方面面。无论如何, 这个在线课程将提供给您怎样进行傅立叶变换运算的基本知识。
能有效和能非常简单地领会的原因是我们使用了一种不太传统的逼近。重要的是你将学习傅立叶变换的要素而完全不用超过加法和乘法的数学计算! 我将设法在不超过以下六节里解释在对音像信号处理中傅立叶变换的实际应用。
步骤 1: 一些简单的前提
在下面,您需要理解以下四件最基本的事情: 加法,乘、除法。什么是正弦,余弦和正弦信号。明显地,我将跳第一二件事和将解释位最后一个。您大概还记得您在学校学过的“ 三角函数”[1] ,它神秘地用于 与角度一起从它们的内角计算它们的边长,反之亦然。我们这里不需要所有这些事,我们只需要知道二个 最重要的三角函数,"正弦" 和"余弦" 的外表特征。这相当简单: 他们看起来象是以峰顶和谷组成的从观察点向左右无限伸展的非常简单的波浪。
(附图一)
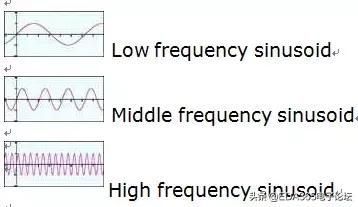
如同你所知道的,这两种波形是周期性的,这意味着在一定的时间、周期之后,它们看起来再次一样。 两种波形看起来也很象,但当正弦波在零点开始时余弦波开始出现在最大值。在实践中,我们如何判定我们在一个给定时间所观测到的波形是开始在它的最大值或在零? 问的好: 我们不能。实践上没有办法区分正弦波和余弦波,因此看起来象正弦或余弦波的我们统称为正弦波,在希腊语中译作"正弦类"。正弦波的一个重要性质是"频率"。它告诉我们在一个给定的时间内有多少个波峰和波谷。高频意味许多波峰和波谷, 低频率意味少量波峰和波谷:
(附图二)
步骤 2: 了解傅立叶定理
Jean-Baptiste Joseph Fourier 是孩子们中让父母感到骄傲和惭愧的的一个,因为他十四岁时就开始对他们说非常复杂的数学用语。他的一生中做了很多重要工作,但最重大的发现可能是解决了材料热传导问题。
他推导出了描述热在某一媒介中如何传导的公式,即用三角函数的无穷级数来解决这个问题(就是我们在上面讨论过的正弦、余弦函数)。主要和我们话题有关的是:傅里叶的发现总结成一般规律就是任意复杂的信号都能由一个个混合在一起的正弦函数的和来表示。
这是一个例子:
(附图三)
在这里你看到的是一个原始的信号,以及如何按某一确定的关系(“ 配方” )混合在一起的正弦函数混合物(我们称它们为分量)所逼近。我们将简略地谈论一下那份配方。如你所知,我们用的正弦函数愈多 其结果就愈精确地接近我们的原始信号波形。在“ 现实” 世界中,在信号连续的地方,即你能以无穷小的间 隔来测量它们,精度仅受你的测试设备限制,你需要无限多的正弦函数才能完美地建立任意一个给定的信 号。幸运地是,和数字信号处理者们一样,我们不是生活在那样的世界。相反,我们将处理仅以有限精度 每隔一定间隔被测量的现实世界的采样信号。因而,我们不需要无限多地正弦函数,我们只需要非常多。 稍后我们也将讨论这个“ 非常多” 是多少。目前重要的一点是你能够想象,任意一个在你计算机上的信号, 都能用简单正弦波按配方组成。
步骤 3: “ 非常多” 是多少
正如我们所知道的,复杂形状的波形能由混合在一起的正弦波所建立。我们也许要问需要多少正弦波来 构造任意一个在计算机上给定的信号。当然,倘若我们知道正在处理的信号是如何组成的,这可能至少是 一个单个正弦波。在许多情况下,我们处理的现实世界的信号可能有非常复杂的结构,以至于我们不能深 入知道实际上有多少“ 分量” 波存在。在这种情况下,即使我们无法知道原始的信号是由多少个正弦波来构 成的,肯定存在一个我们将需要多少正弦波的上限。尽管如此,这实际上没解决有多少的问题。让我们试 着来直观地逼近它: 假设一个信号我们有 1000 个样采,可能存在的最短周期正弦波(即多数波峰波谷在其 中)以交替的波峰波谷分布在每个采样内。因此,最高频率的正弦波将有 500 个波峰和 500 个波谷在我 们的 1000 个采样中,且每隔一个采样是波峰。下图中的黑点表示我们的采样,所以,最高频率的正弦波 以看起来象这样:
The highest frequency sine wave(附图四)
现在让我们来看一下最低频率正弦波可能多么低。如果我们只给一个单独的采样点,我们将如何能测量穿过这点的正弦波的峰顶和谷? 我们做不到,因为有许多不同周期正弦波穿过这点。
(附图五)
所以,一个单独数据点不足以告诉我们关于频率的任何事。现在,如果我们有两个采样,那么穿过这 两点的正弦波的最低频率是什么?在这种情况下它很常简单。只有一个穿过这两点的非常低频率的正弦 波。它看起来向这样:
The lowest frequency sine wave(附图六)
想象最左面的两个点是二个钉子和一个跨越它们之间的弦(图六描述三个数据点是因为正弦波的周期性,但我们实际上只需要最左面的两点说明它的频率)。我们能领会的最低的频率是来回地摆动在二个钉 子之间的弦,象是图六中左边两点之间的正弦波所做的。如果我们有 1000 个采样,那么两个“ 钉子” 相当 于第一个或最后的采样,比如 1 号采样和 1000 号采样。从对乐器的体验我们知道,当长度增加时弦的频 率将下降。所以我们可以想象,当我们将两个钉子向彼此远离的方向移开时,最小正弦波的频率将变得更 低。例如,如果我们选择 2000 个采样,因为我们的“ 钉子” ,在 1 号或 2000 号采样间,所以最低正弦波将 更低。事实上,它将低两倍,因为因为我们的钉子比 1000 个采样时远两倍。这样,如果我们有更多的采 样,我们将能辨别出一个更低频率的正弦波,因为它们的零交叉点(我们的“ 钉子” )将移动得更远。这对 了解下面的解释是非常重要的。
象我们看到的那样,在两个“ 钉子” 之后,我们的波形开始重复上升斜坡(第一个钉子和第三个钉子同样)。这意味着任意两个相邻的钉子准确地包含完整正弦波的一半,换句话说一个峰或一个谷或半个周期。
概括一下我们刚学过的东西,我们知道,一个采样正弦波的上限频率是所有其它有一个波峰和波谷的 采样,并且,低频下限是我们看到的正好匹配采样数的正弦波的周期的一半。但等一下,这难到不意味着, 当上限频率保持固定时,当有很多采样时最低频率可以降低?确实如此! 结果我们将从一个低频开始增加 更多正弦波来组成一个较长的未知内容的信号。
一切都清楚了,但我们仍然不知道我们最终需要多少正弦波。就象我们现在知道任意正弦波分量所能 具的有上下限频率一样,我们能计算出适合这两个极限之间的量是多少。既然我们沿着最左到最右的采样 固定了最低正弦波分量,我们要所有其它正弦波最好也使用这些钉子(为什么我们要不同地对待他们? 所有的正弦波被同等的创建!)。假设正弦波束是系在吉他上二个固定点的弦。它们能只摇摆在二个钉子之间(除非他们断了),就象我们下图的正弦波。这导致如下关系,我们的最低分量(1)以 1/2 周期装配,第二分量(2)以 1 个周期装配,第三分量以 1 1/2 周期装配以此类推直到我们看到的 1000 个采样。形象地, 看起来象这:
(附图七)
在,如果我们算一下要多少正弦波以那种方法装配我们的 1000 个采样,就会发现我们精确地需要1000 个正弦波叠加起来表示 1000 个采样。实际上,我们总是发现我们需要和采样一样多的正弦波。
步骤 4 关于烹饪食谱
在前面的段落我们看到, 任一个给定的在计算机上的信号能被正弦波混合物来构造。 我们考虑了他们的频率,并且考虑了需要多大的最低和最高频率的正弦波来完美地重建任一个我们所分析信号。我们明白 了为确定所需最低的正弦波分量,我们考察的采样的数量是重要,但我们还未论述实际正弦波如何必需被 混合产生某一确定的结果。由叠加正弦波组成任何指定的信号,我们需要测量他们的另外一个方面。实际 上,频率不是我们需要知道的唯一的事。我们还需要知道正弦波的幅度,也就是说每个正弦波幅度有多高 才能混合在一起产生我们需要的输入信号。高度是正弦波的峰顶的高度,意即峰顶和零线之间距离。幅度 赿高,我们听到的声音也就赿大。所以,如果您有一个含有许多低音的信号,无疑可以预期混合体中的低 频率正弦波的分量比例比高频正弦波分量更大。因此一般情况下,低音中的低频正弦波有一个比高频正弦 波更高的幅度。在我们的分析中,我们将需要确定各个分量正弦波的幅度以完成我们的配方。
步骤 5:关于苹果和桔子
如果你一直跟着我,我们几乎完成了通向傅里叶变换的旅程。我们学了需要多少正弦波,它的数量依 赖于我们查看的采样的数量有一个频率上下限界,并且不知道怎么确定单个分量的幅度以完成我们的配 方。我们一直不清楚究竟如何从我们的采样来确定实际的配方。直观上我们可以断定能找到正弦波的幅度, 设法把一个已知频率正弦波和采样作对比,我们测量找出它们有多么接近。如果它们精确地相等,我们知 道该正弦波存在着相同的幅度,如果我们发现我们的信号与参考正弦波一点也不匹配,我们将认为这个不 存在。尽管如此,我们如何高效地把一个已知的正弦波同采样信号进行比较?幸运地是,数字信号处理工 作者早已解决了如何作这些。事实上,这象加法和乘法一样容易-我们取一个已知频率的单位正弦波(这意味着它的振幅是 1,可从我们的计算器或计算机中精确地获得)和我们的信号采样相乘。累加乘积之后, 我们将得到我们正在观测的这个频率上正弦波分量的幅度。
这是个举例,一个简单的完成这些工作的 C 代码片段:
Listing 1.1: The direct realization of the Discrete Sine Transform (DST):
#define M_PI 3.14159265358979323846
long bin,k;
double arg;
for (bin = 0; bin < transformLength; bin++) {
transformData[bin] = 0.;
for (k = 0; k < transformLength; k++) {
arg = (float)bin * M_PI *(float)k / (float)transformLength;
transformData[bin] += inputData[k] * sin(arg);
}
}
这段代码变换存储在 inputData[0...transformLength-1]中我们测量的采样点成为一个正弦波分量的幅度队列 transformData[0...transformLength-1]。根据通用术语,我们称参考正弦波的频率步长为盒(bin),
这意味着它们被认为象是一个我们放置我们估计的任意分量波的幅度的容器。离散正弦变换(DST)是一个普通程序,它假设我们无法想象我们的信号看起来象什么样,否则我们能使用一个更加高效率的方法来确 定正弦波分量的幅度(例如,我们予先知道, 我们的信号是一个已知频率的正弦波。我们能直接地找出它 的高度而不用计算正弦波的整个范围。实现这个有效的逼近是基于傅里叶原理,它能在文献的戈策尔(Goe rtzel)算法条目下找到)。
这些就是你坚持想要的我们为什么用这样的方法计算正弦变换的一个解释:对我们用一个已知频率正弦 波的乘积来作一种非常直观逼近的理由,可以设想,这大致相当于一个固有频率的“ 共振” 在系统内发生时 物理世界发生的事情。sin(arg)项本质上是一个获得由输入信号波形激励的谐振器。如果输入(信号)有在 我们正观测的频率上的分量,它的输出将是参考正弦波谐振的幅度。因为我们的参考波是单位幅度的,输出是一个在那个频率上的分量的实际幅度的一个直接测量。因为谐振器只是简单的滤波器,变换(不可否 认是在稍微宽松条件下)被认为有极窄的带通滤波器组的特征,它位于我们估值的频率中心的周围。这有 助于解释一个事实,为什么傅立叶变换提供了对信号进行过滤的一个高效工具。
只是为了完备性: 当然,上述程序是可逆的,当我们知道它的正弦波分量时,我们的信号(在数字精确度 极限内)能完全被重建,通过简单地把正弦波加起来。这留下给读者做为一个练习。同样程序能改变使用余 弦波做为基本函数工作-我们只需简单地改变 sin(arg)条件到 cos(arg)来获得离散余弦变换的直接实现(DC T)。
现在,就象在这篇文章较前面的段落中我们讨论过的那样,我们在实践中没有办法区分一个被测量的正 弦类函数象是正弦波还是余弦波。做为代替我们总是测量正弦信号,且正弦和余弦变换在实践中没有太大 的用途,除了一些特殊情况(象图象压缩的地方,即毎块图象具有能用一个基本的余弦或正弦函数较好模 拟特性,例如能用余弦基本函数较好表现的相同颜色的大区域)。正弦信号是一个比正弦或余弦波更一般 的片断,因为它可以开始在在它的周期中的一个任意位置。我们记得,当余弦波开始于 1 时,正弦波总开 始在 0。 当我们采取正弦波作为参考,余弦波开始在它的周期的最后 1/4 之处。一般用度或弧度测量它们 的偏移量,这是两个一般与三角函数相关的单位。一个完整的周期等于 360°(代表 "度") 或 2π 个弧度(代表"2π" ,"π" 发音象“pie” 。π 是希腊字表示数 3.14159265358979323846... 在三角学方面有重要意义) 。
余弦波因而有一个 90°或 π/2 的偏移。这偏移叫正弦信号的相位,因此余弦波相对正弦信号有 90°或 π/2 相位。
相位的事情就有这些内容。因为我们一直不能限定信号在 0°或 90°相位开始(因为我们正观测一个我们 可能无法控制的信号),它对同时直接唯一的描述信号的频率、振幅、相位至关重要。以正弦或余弦做变换相位限制在 0°或 90°,一个具有任意相位的正弦信号将引起相邻频率出现假峰(因为它们试图“ 帮助” 分析,强制给被测信号加上一个 0°或 90°的相位作用)。它有些象用一圆石头去填满一个方孔:你需要小一 些的圆石头去填充剩余的空间,并且更小的石头填好依然留出空的空间,等等。我们所需要的是能处理一 般信号的变换,它能处理任意相位正弦波构成的信号。
步骤 6:离散傅叶变换
从正弦变换到傅里叶变换的步骤是简单的,只需用更一般的方法。在正弦变换中对每个频率上的测度 使用正弦波,在傅里叶变换中正弦、余弦波二者都使用。就是说,对任意的当前频率,我们以同一频率的 正弦和余弦波来“ 比较” (或“ 共振” )被测信号。如果我们的信号看起来很象正弦波,变换的正弦部份将有 一个大的幅值。如果它看起来象余弦波,变换的余弦部份将有一个大的幅值。如果看起来象反相的正弦波, 也就是说,它开始于 0 但下降至-1 取代上升至 1,它的正弦部份将有一个大的负幅值。这表明用+、- 符号和正弦、余弦相位能表示任意给定频率的正弦信号[2]。
Listing 1.2: The direct realization of the Discrete Fourier Transform[3]:
#define M_PI 3.14159265358979323846
long bin, k;
double arg, sign = -1.; /* sign = -1 -> FFT, 1 -> iFFT */
for (bin = 0; bin <= transformLength/2; bin++) {
cosPart[bin] = (sinPart[bin] = 0.);
for (k = 0; k < transformLength; k++) {
arg = 2.*(float)bin*M_PI*(float)k/(float)transformLength;
sinPart[bin] += inputData[k] * sign * sin(arg);
cosPart[bin] += inputData[k] * cos(arg);
}
}
我们仍遗留着一个问题,就是如何获得傅里叶变换所缺乏的那些有用的东西。我说过傳里叶变换的优赿性超过正弦和余弦变换是因为用正弦信号工作。但至今我们还未看到任何正弦信号,仍只有正弦和余弦。好,这需要一点附加处理步聚:
#define M_PI 3.14159265358979323846
long bin;
for (bin = 0; bin <= transformLength/2; bin++) {
/* frequency */
frequency[bin] = (float)bin * sampleRate / (float)transformLength;
/* magnitude */
magnitude[bin] = 20. * log10( 2. * sqrt(sinPart[bin]*sinPart[bin] + cosPart[bin]*c
osPart[bin]) / (float)transformLength);
/* phase */
phase[bin] = 180.*atan2(sinPart[bin], cosPart[bin]) / M_PI - 90.;
}
在运行清单 1.3 所示的关于 DFT 输出的代码段之后,我们结束被看作以正弦信号波的和的输入信号表示。
K 序正弦信号是用 frequency[k],magnitude[k]和 phase[k]来描述的。单位是 Hz(Hertz,周/秒),dB(Decibel),和°(Degree)。请注意在经过清单 1.3 的后加工(处理)即把正弦和余弦函数部份转换成一个单一的正弦信 号之后,我们命名 K 序正弦信号的振幅-DFT 存贮为幅度,且它总是取相对值。我们可以说一个-1.0 的振 幅对应于 1.0 的幅度,对应于相位+或-180°。在文献中,做做傅里叶变换的场合,队列 magnitude[] 被称 作被测信号的幅度谱,队列 phase[]被称作被测信号的相位谱。
如用分贝测量存贮幅度的参考,输入波也期望有一个在[-1.0,1.0]之间的采样值,相对于 0dB 幅度满刻 度数字。做为一个 DFT 的有趣应用,比如清单 1.3 就可被用于写一个基于离散傅里叶变换的谱分析。
结论
象我们已知那样,傅里叶变换和其系列的离散正弦和余弦变换,提供了把一个信号分解成一束分波的 便利工具。结果有正弦或余弦之一,或正弦信号(用正弦和余弦波的组合来描述)。在傅里叶变换中同时 使用正弦和余弦波的好处是我们因而能引入相位的概念,它使变换更一般化,因而我们能用它有效清楚地 分析既不是纯正弦也不是纯余弦的正弦信号,当然其它信号也一样。
傅里叶变换与被考察信号无关,因而无论我们正分析的信号是一个正弦信号或是一些其它的更复杂的, 变换需要相同的操作数。这就是为什么傅里叶变换被称做无参数变换的原因,这意味着它对需要的信号“ 智能的” 分析没有直接的帮助(在考察一个我们已知是一个信号是正弦曲线的情况下,我们更喜欢精确地获 得关于相位,频率,幅度的信息以代替一串在一些预定频率上的正弦和余弦波)。
现在我们也知道了我们是在求输入信号在一组固定频率栅格上的值,输入信号实际存在的频率组在这 组栅格上可能不起作用。我们在分析中利用的栅格是人为的,因为我们几乎按照关于它们的频率的尝试来 选择参考正弦、余弦波。说到了这些,马上清楚了一个将要很容易遇到的要点,即被测信号的频率位于变 换栅格的频率之间。因此,有一个频率发生在位于两个频率栅格之间的正弦曲线,在变换中将不好被描述。 包围着与输入信号频率最接近的栅格的相邻的栅格将试图‘改正’ 频率的背离。因而,输入信号的能量将拖 尾至数个相邻的栅格。这也是傅里叶变换不能迅速地分析声音返回它的基波和谐波(并且,这也是为什么 我们称正弦和余弦波为分波而不谐波和泛音)。
简单的说,没有进一步的快速处理,DFT 和一个狭窄的坝一样,细小并行的带通滤波器组(“ 通道” )和每个通道带有附加的相位信息。这对分析信号、做滤波器和运用其它的技巧是有益的(改变一个信号的 音调而不改变它的速度是它们其中之一,说明在 DSPdimension.com 上另一篇不同的文章中),但它需 要对少量普通任务附加快速处理。同样,它能被认为是使用除了正弦和余弦波基本函数的变换系列的一个 特例。在这个方向上展开概念超出了这篇文章的范围。
最后,重要的是要提及一个更高效的 DFT 工具,也就是一个被称做快速傅里叶变换的算法。它最初 是由库利和图克在 1969 年构思的(它的根源仍然要追溯到高斯和其它人的工作)。FFT 只是一个高效的 算法,它比上面给出的以直接逼近计算 DFT 所化的时间少,它是结果完全相同的其它方法。无论如何,F FT 是以库利/图克算法实施的,它需要变换长度是 2 的幂。在实践中,对大多数应用来说这是一个可以接 受的限制。有大量的以不同方法实施 FFT 的可利用的文献,因而,可以说有足够多不同的 FFT 实现,其中一些并不需要经典 FFT 的 2 的幂的限制。
下面清单 1.4 以程序 smbFft()给出了一个 FFT 的实现。
Listing 1.4: The Discrete Fast Fourier Transform (FFT):
#define M_PI 3.14159265358979323846
void smbFft(float *fftBuffer, long fftFrameSize, long sign)
/*
FFT routine, (C)1996 S.M.Bernsee. Sign = -1 is FFT, 1 is iFFT (inverse)
Fills fftBuffer[0...2*fftFrameSize-1] with the Fourier transform of the time domain data in fftBuffer
[0...2*fftFrameSize-1]. The FFT array takes and returns the cosine and sine parts in an interleaved
manner, ie. fftBuffer[0] = cosPart[0], fftBuffer[1] = sinPart[0], asf. fftFrameSize must be a power of
2. It expects a complex input signal (see footnote 2), ie. when working with 'common' audio sig
nals
our input signal
has to be passed as {in[0],0.,in[1],0.,in[2],0.,...} asf. In that case, the transform
of
the frequencies of
interest is in fftBuffer[0...fftFrameSize].
*/
{
float wr, wi, arg, *p1, *p2, temp;
float tr, ti, ur, ui, ur, ui, *p1r, *p1i, *p2r, *p2i;
long i, bitm, j, le, le2, k;
for (i = 2; i < 2*fftFrameSize-2; i += 2) {
for (bitm = 2, j = 0; bitm < 2*fftFrameSize; bitm <<= 1) {
if (i & bitm) j++;
j <<= 1;
}
if (i < j) {
p1 = fftBuffer+i; p2 = fftBuffer+j;
temp = *p1; *(p1++) = *p2;
*(p2++) = temp; temp = *p1;
*p1 = *p2; *p2 = temp;
}
}
for (k = 0, le = 2; k < (long)(log(fftFrameSize)/log(2.)); k++) {
le <<= 1;
le2 = le>>1;
ur = 1.0;
ui = 0.0;
arg = M_PI / (le2>>1);
wr = cos(arg);
wi = sign*sin(arg);
for (j = 0; j < le2; j += 2) {
p1r = fftBuffer+j; p1i = p1r+1;
p2r = p1r+le2; p2i = p2r+1;
for (i = j; i < 2*fftFrameSize; i += le) {
tr = *p2r * ur - *p2i * ui;
ti = *p2r * ui + *p2i * ur;
*p2r = *p1r - tr; *p2i = *p1i - ti;
*p1r += tr; *p1i += ti;
p1r += le; p1i += le;
p2r += le; p2i += le;
}
tr = ur*wr - ui*wi;
ui = ur*wi + ui*wr;
ur = tr;
}
}
}