BZOJ 2658 小蓝的好友
题目链接:http://www.lydsy.com:808/JudgeOnline/problem.php?id=2658
题意:给出一个n*m的格子。某些格子中有障碍。求包含至少一个障碍的矩形有多少个?
思路:我们求空白矩形的个数。
从上到下一行一行计算,每到达一行,计算以该行为底的空白矩形个数。我们只需要知道每列向上延伸的最大距离。
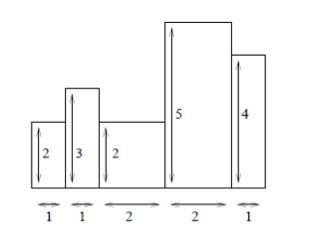
这个可以看做是一棵树
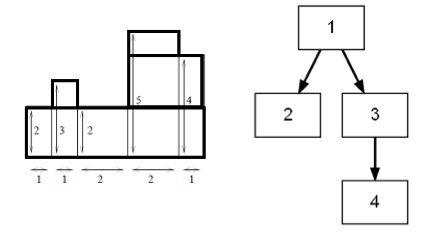
我们只需要记录每个的高度即可。
那么每次增加一行,若整行都没有障碍,则根节点的高度增加1.否则,障碍将树分为若干子树。这个操作可以用fhq treap实现,即通过树的分离和合并实现所有操作。
合并两个子树AB时,要求A的所有元素小于B。或者将A设为B的左孩子,或者将B设为A的右孩子。这个操作比较简单。
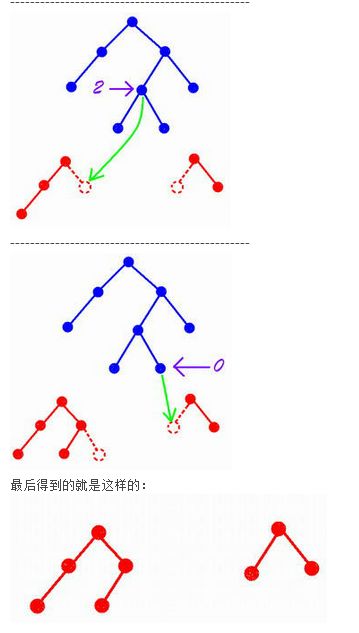
对于分离操作,用split(now,x,y,K)表示,将now为根的子树的前K个孩子分离,分开后的两个子树的根分别是x,y
设K=5

分离红色圈住的5个节点,过程如下:
(这个图来自http://hi.baidu.com/wdxertqdtscnwze/item/7b6a9419be7c68cd756a8498)

const int N=100005;
struct node
{
int c[2],h,det,size;
i64 ans;
void add(int x)
{
h+=x;
det+=x;
}
};
node a[N];
int root;
#define C2(x) ((x)*((x)+1)/2)
void pushUp(int t)
{
if(!t) return;
a[t].size=1;
a[t].ans=0;
for(int i=0;i<2;i++) if(a[t].c[i])
{
int p=a[t].c[i];
a[t].size+=a[p].size;
a[t].ans+=a[p].ans;
a[t].ans+=(i64)(a[p].h-a[t].h)*C2(a[p].size);
}
}
void pushDown(int t)
{
if(!t||!a[t].det) return;
if(a[t].c[0]) a[a[t].c[0]].add(a[t].det);
if(a[t].c[1]) a[a[t].c[1]].add(a[t].det);
a[t].det=0;
}
pair<int,int> split(int u,int k)
{
if(!u) return MP(0,0);
pushDown(u);
if(a[a[u].c[0]].size+1<=k)
{
k-=a[a[u].c[0]].size+1;
pair<int,int> tmp=split(a[u].c[1],k);
a[u].c[1]=tmp.first;
pushUp(u);
return MP(u,tmp.second);
}
else
{
pair<int,int> tmp=split(a[u].c[0],k);
a[u].c[0]=tmp.second;
pushUp(u);
return MP(tmp.first,u);
}
}
int merge(int u,int v)
{
if(!u||!v) return u+v;
pushDown(u);
pushDown(v);
if(a[u].h<a[v].h)
{
a[u].c[1]=merge(a[u].c[1],v);
pushUp(u);
return u;
}
else
{
a[v].c[0]=merge(u,a[v].c[0]);
pushUp(v);
return v;
}
}
pair<int,int> b[N];
int n,m,K;
int main()
{
n=myInt();
m=myInt();
K=myInt();
for(int i=1;i<=K;i++)
{
b[i].first=myInt();
b[i].second=myInt();
}
sort(b+1,b+K+1);
for(int i=1;i<=m;i++)
{
root=merge(root,i);
pushUp(root);
}
int cur=1;
i64 ans=(i64)C2(n)*C2(m);
for(int i=1;i<=n;i++)
{
a[root].add(1);
while(cur<=K&&b[cur].first==i)
{
pair<int,int> tmp1=split(root,b[cur].second-1);
pair<int,int> tmp2=split(tmp1.second,1);
a[tmp2.first].h=0;
root=merge(tmp1.first,tmp2.first);
root=merge(root,tmp2.second);
cur++;
}
ans-=a[root].ans;
ans-=(i64)a[root].h*C2(a[root].size);
}
printf("%lld\n",ans);
}