图解seq2seq+attention机制

seq2seq 是一个Encoder–Decoder 结构的网络，它的输入是一个序列，输出也是一个序列， Encoder 中将一个可变长度的信号序列变为固定长度的向量表达，Decoder 将这个固定长度的向量变成可变长度的目标的信号序列。–简书

一、注意力机制Attention

任务：德文翻译为英文

先讲解Encoder部分的注意力机制

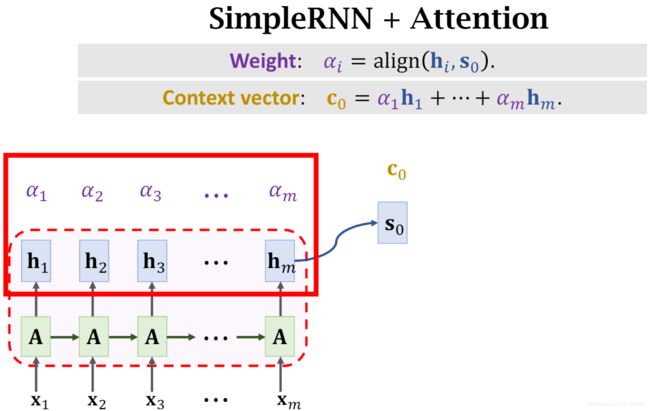
$x_i$：表示输入的每一个德文单词（严谨的说，应该是德文单词的向量表示word_embedding）
A：Encoder，隐藏层，可以是GRU、LSTM、RNN
$h_i$：每个时刻最后一层生成的隐藏层状态
$h_m$：最后一层最后时刻生成的隐藏层状态
$s_0$：数值上=$h_m$，在此记为换个名字
${\alpha }_i$：$s_0$与$h_i$的"相似度"（相关性）的权重表示
Weight: ${\alpha }_i$=align($s_0$,$h_i$)

计算得到 m 个相关性αi之后，将这些值与hi进行加权平均

$c_0={\sum }_{i=1}^m{\alpha }_i{h}_i={\alpha }_1{h}_1+\cdot \cdot \cdot {\alpha }_m{h}_m$

$c_0$称为context vector ，上下文背景变量

• 简单说明一下计算$c_0$的原因：
  对于那些权重比较大的${\alpha }_k$，最终$c_0$中也会有一大部分来自于 ${\alpha }_k$。 $c_0$实际上考虑到了所有时刻的隐藏层变量h，而h又是输入的x的表示。也就是说$c_0$考虑了所有的输入，但对于重要的输入时刻关注得更多，而某些时刻关注的更少，这就是注意力机制。

接下来讲解Decoder部分的注意力机制

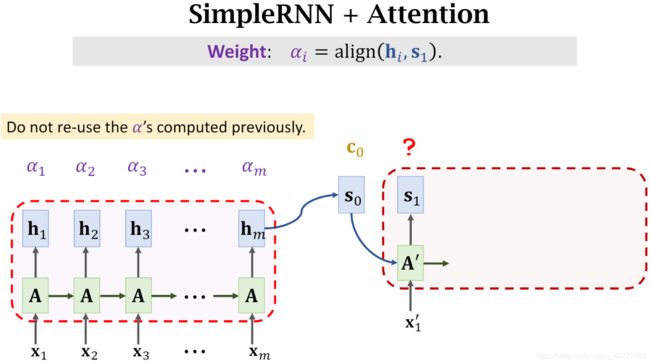
$x_i^{’}$：表示正确的的英文单词翻译输入
$A^{’}$：Decoder隐藏层，也是RNN或RNN的变种
$s_0$：在Encoder部分计算得到的

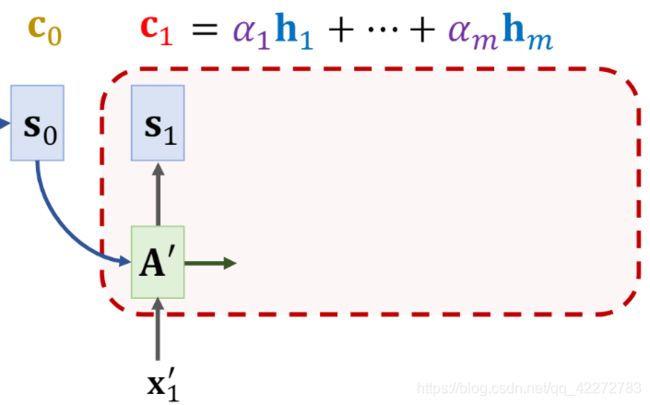
将$s_0,c_0,x_1^{’}$作为$t_0$时刻 Decoder 的输入,计算得到$s_1$,然后再计算$s_1$与所有$h_i(i=1,...,m)$之间新的相关性${\alpha }_i$

同样的，将新计算得到的${\alpha }_i$与$h_i$做加权平均，得到新的 context vector $c_1$

重复上述步骤，直到 Decoder 结束

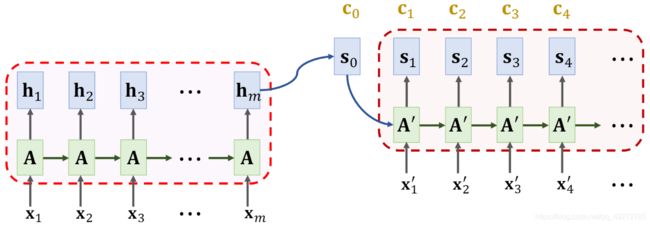
ps:简化版的Decoder也可能没有多次计算context vector ci,而是用c0一以贯之。

二、编码器 — 解码器

编码器和解码器分别对应输入序列和输出序列的两个循环神经网络。我们通常会在输入序列和输出序列后面分别附上一个特殊字符（end of sequence）表示序列的终止。在测试模型时，一旦输出就终止当前的输出序列

二（1）、编码器Encoder

注：context vextor：称背景向量、上下文向量、上下文背景向量

编码器的作用是把一个不定长的输入序列转化成一个定长的背景词向量c。该背景词向量包含了输入序列的信息。常用的编码器是循环神经网络。
假设$x_t$是单个输出在嵌入层的结果，即输入。
隐藏层变量为

${\mathbf{h}}_t=f({\mathbf{x}}_t,{\mathbf{h}}_{t-1})$

编码器的上下文背景向量为

$\mathbf{c}=q({\mathbf{h}}_1,\dots ,{\mathbf{h}}_T)$

一个简单的背景向量可以认为是该网络最终时刻的隐藏层变量 。我们将这里的循环神经网络叫做编码器。
当我们希望编码器的输入既包含正向传递信息又包含反向传递信息时，我们可以使用双向循环神经网络：
如果输入序列是 ，在正向传递中${\mathbf{x}}_1,{\mathbf{x}}_2,...,{\mathbf{x}}_T$，隐藏层变量为：

${\mathbf{h}}_t=f({\mathbf{x}}_t,{\mathbf{h}}_{t-1})$

而反向传递过程中${\mathbf{x}}_T,{\mathbf{x}}_T-1,...,{\mathbf{x}}_1$，隐藏层变量的计算变为:

${\mathbf{h}}_t=f({\mathbf{x}}_t,{\mathbf{h}}_{t-1})$

此时的隐藏层变量为：

${\mathbf{h}}_t=f({\mathbf{h}}_{t-1},{\mathbf{h}}_{t-1})$

二（2）、解码器Decoder

编码器最终输出了一个上下文背景向量c，该背景向量整合了输入序列${\mathbf{x}}_1,{\mathbf{x}}_2,...,{\mathbf{x}}_T$
假设训练数据中的输出序列是${\mathbf{y}}_1,{\mathbf{y}}_2,...,{\mathbf{y}}_{T^{\prime }}$，我们希望表示每个$t^{’}$时刻输出的向量，既取决于之前的输出又取决于背景向量。因为，我们可以最大化输出序列的联合概率

$P({\mathbf{y}}_1,{\mathbf{y}}_2,...,{\mathbf{y}}_{T^{\prime }})={\prod }_{t^{\prime }=1}^{T^{\prime }}P({\mathbf{y}}_{t^{\prime }}\mid {\mathbf{y}}_1,...,{\mathbf{y}}_{t^{\prime }-1},\mathbf{c})$

为此，我们使用另一个循环神经网络作为解码器。解码器使用函数p来表示单个输出${\mathbf{y}}_{t^{\prime }}$的概率

$P({\mathbf{y}}_{t^{\prime }}\mid {\mathbf{y}}_1,...,{\mathbf{y}}_{t^{\prime }-1},\mathbf{c})=p({\mathbf{y}}_{t^{\prime }-1},{\mathbf{s}}_{t^{\prime }},\mathbf{c})$

其中的${\mathbf{s}}_{t^{\prime }}$为${\mathbf{t}}^{\prime }$时刻的解码器的隐藏层变量。该隐藏层变量

${\mathbf{s}}_{t^{\prime }}=g({\mathbf{y}}_{t^{\prime }-1},\mathbf{c},{\mathbf{s}}_{t^{\prime }-1})$

其中函数 g 是循环神经网络单元。

需要注意的是，编码器和解码器通常会使用多层循环神经网络

图解attention