脑机接口实例二：脑电信号CSP处理

---

前言

本文在实例一的基础之上，选用BCI大赛08年数据集，基于CSP的特征提取，运用AdaBoost算法进行集成分类，以期实现运动想象中左、右手动作脑电信号的分类。

---

一、实例说明

1.1 期望目标

• 掌握数据集预处理的方法
• 实际运用CSP算法进行特征提取
• 对提取的特征进行boosting分类（AdaBoost是其中一种）

1.2 数据解读

1. 实验范式

      数据集由9名受试者的脑电图数据组成。BCI范式由四个不同的运动想象任务组成，即左手(类别1)、右手(类别2)、双脚(类别3)和舌头(类别4)的运动想象。范式记录不同日期的两天数据。（每天6圈，每圈48trails）。（共计576个trails，每个任务144trails）
      正式范式之前，记录5分钟估计EOG值，分三块：看屏幕上的十字（2分钟）、闭眼（1分钟）、眼动（1分钟），注：由于技术问题被试A04T的眼动数据较短，仅包含眼动状态。如下图所示：

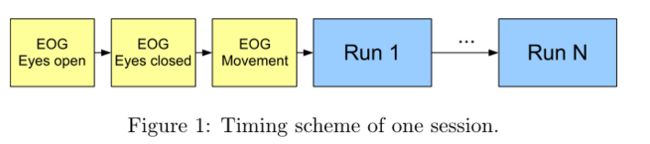
      被试者坐在电脑屏幕前面的舒适的扶手椅上，在试验开始时(t=0s)，黑屏上出现了一个十字。此外，还提出了一种短声告警音。两秒后（t=2s），以箭头的形式指向左、右、下或上（对应于四个类中左手、右手、脚或舌头的一个）的提示，出现在屏幕上1.25秒。这促使受试者完成所需的运动想象任务。不提供任何反馈。被试在t=6s时被要求执行运动想象任务，直到屏幕上的十字消失为止。随后屏幕再次为黑色的短暂中断，流程如下图所示：（有效数据为2-6s，即运动想象任务记录区间，亦为需提取数据的区间）

2. 数据记录

      250Hz采样，并在0.5Hz和100Hz之间进行带通滤波。除了22个脑电图通道，3个单极EOG通道，以250Hz的频率记录和采样(见下图)。它们在0.5Hz和100Hz之间进行带通滤波，放大器的灵敏度设置为1mV。EOG通道是为伪像处理方法的后续应用提供的，不得用于分类。

3. 数据文件描述

      事件类型描述如下 （event type 769/770 对应左右手的动作，以此为基准进行数据提取） ：

二、实例代码及结果分析

2.1 MATLAB代码

主函数(main):

clc;clear;

%% 读取数据并对数据预处理

Subjects = 9;      %被试数
Fs = 250;          %采样率
windowLength = 4;  %单次采样时间
chanSelect = [8,10,12]; %通道选择c3,c4,cz
totalFlt = [4 40]; %总的滤波频段选择

load rawdata1.mat
[Data_train,label_train] = preProccess(Fs,windowLength,EEG,chanSelect,totalFlt); %preProccess执行数据提取、分段、滤波处理

load rawdata2.mat
[Data_test,label_test] = preProccess(Fs,windowLength,EEG,chanSelect,totalFlt);

%% CSP特征提取

EEGSignals.x = Data_train;
EEGSignals.y = label_train;
Y = label_train;

classLabels = unique(EEGSignals.y); 
CSPMatrix = learnCSP(EEGSignals,classLabels);
nbFilterPairs = 1;
X = extractCSP(EEGSignals, CSPMatrix, nbFilterPairs); 

EEGSignals_test.x=Data_test;
EEGSignals_test.y=label_test;
T = extractCSP(EEGSignals_test, CSPMatrix, nbFilterPairs); 

save dataCSP.mat X Y T


color_L = [0 102 255] ./ 255;
color_R = [255, 0, 102] ./ 255;

pos = find(Y==1);
plot(X(pos,1),X(pos,2),'x','Color',color_L,'LineWidth',2);

hold on
pos = find(Y==2);
plot(X(pos,1),X(pos,2),'o','Color',color_R,'LineWidth',2);

legend('Left Hand','Right Hand')
xlabel('C3','fontweight','bold')
ylabel('C4','fontweight','bold')

CSP算法：

function CSPMatrix = learnCSP(EEGSignals,classLabels)
%
%Input:
%EEGSignals: the training EEG signals, composed of 2 classes. These signals
%are a structure such that:
%   EEGSignals.x: the EEG signals as a [Ns * Nc * Nt] Matrix where
%       Ns: number of EEG samples per trial
%       Nc: number of channels (EEG electrodes)
%       nT: number of trials
%   EEGSignals.y: a [1 * Nt] vector containing the class labels for each trial
%   EEGSignals.s: the sampling frequency (in Hz)
%
%Output:
%CSPMatrix: the learnt CSP filters (a [Nc*Nc] matrix with the filters as rows)
%
%See also: extractCSPFeatures

%check and initializations
nbChannels = size(EEGSignals.x,2);
nbTrials = size(EEGSignals.x,3);
nbClasses = length(classLabels);

if nbClasses ~= 2
    disp('ERROR! CSP can only be used for two classes');
    return;
end

covMatrices = cell(nbClasses,1); %the covariance matrices for each class

%% Computing the normalized covariance matrices for each trial
trialCov = zeros(nbChannels,nbChannels,nbTrials);
for t=1:nbTrials
    E = EEGSignals.x(:,:,t)';                       %note the transpose
    EE = E * E';
    trialCov(:,:,t) = EE ./ trace(EE);
end
clear E;
clear EE;

%computing the covariance matrix for each class
for c=1:nbClasses      
    covMatrices{c} = mean(trialCov(:,:,EEGSignals.y == classLabels(c)),3); %EEGSignals.y==classLabels(c) returns the indeces corresponding to the class labels  
end

%the total covariance matrix
covTotal = covMatrices{1} + covMatrices{2};

%whitening transform of total covariance matrix
[Ut Dt] = eig(covTotal); %caution: the eigenvalues are initially in increasing order
eigenvalues = diag(Dt);
[eigenvalues egIndex] = sort(eigenvalues, 'descend');
Ut = Ut(:,egIndex);
P = diag(sqrt(1./eigenvalues)) * Ut';

%transforming covariance matrix of first class using P
transformedCov1 =  P * covMatrices{1} * P';

%EVD of the transformed covariance matrix
[U1 D1] = eig(transformedCov1);
eigenvalues = diag(D1);
[eigenvalues egIndex] = sort(eigenvalues, 'descend');
U1 = U1(:, egIndex);
CSPMatrix = U1' * P;

2.2 运行结果及分析

1. CSP特征提取
   
   

图一，由算法代码进行预处理数据后得到的CSP特征提取结果
图二，由导入eeglab进行预处理数据后得到的CSP特征提取结果

        分析： 由上图，我们可以看出，当前CSP算法对数据进行了一定程度的特征提取，但特征之间并没有达到理想的分离程度，部分数据集中纠缠在一起。产生此结果的可能原因：（1）数据提取、预处理阶段存在不足；（2）该CSP算法自身存在缺陷（如本实例将导联关系限制在C3、C4、CZ三个通道，与其他通道导联的相关性难以体现）。针对可能原因1，我将数据导入eeglab，用eeglab自身的预处理功能，对数据进行预处理操作，再应用CSP算法进行特征提取，但实验结果同样不理想，如图二所示。于是，猜想出现不理想结果可能更多的是原因2造成的，接下来，我将尝试应用不同的方法，对特征进行提取。

2. AdaBoost集成分类
   

        分析： 从CSP提取的特征中，选择144个数据点组成训练集，进行30次迭代集成分类，由图可以看出，随着迭代次数的增加，训练错误率在降低，即分类准确率在提高。尽管如此，分类的错误率仍超过30%，结果并不理想，也在侧面说明，CSP算法存在问题，有进一步改进的空间。

三、问题与反思

• 数据预处理的实际应用能力较弱。例如，在对数据进行分段提取，标签定义，以及应用IIR 滤波，ICA眼电信号去除进行数据预处理的过程中，由于对数组的理解不够准确，时常报错；
• CSP特征提取算法掌握不足，实际应用中，对代码的理解尚浅薄，不能灵活应用和变通；
• 反思：理论知识结合到实际应用中的能力有待加强，接下来，会尝试采用不同的算法实现脑电信号的分类任务，进一步在实践中，加深对算法的理解、掌握。

四、下一阶段计划

• 实例结果的分析表明，当前CSP算法进行特征提取的效果不够理想，有进一步改进的空间，下一阶段计划将围绕这个主题展开。
• 任务一：尝试采用不同的算法，对特征进行提取，以期得到更好的实验结果。
• 任务二：脑机接口理论知识储备不足，尝试系统性学习相关知识。
• 任务三：加强相关算法的学习与应用（分类算法掌握尚浅）。

本文源码：
链接：https://pan.baidu.com/s/1TzEskR1vP4TMx64aTOHRBg （百度网盘）
提取码：muda