小波神经网络整定PID仿真建模
小波（wavelet）神经网络：
由于傅里叶分析是一种时域与频域的全局变换，无法描述信号的局部性质。运用时间-尺度分析方法，小波变换可以多分辨分析和表述信号的局部特征。
若
，即
则可以看作的能量是有限的。
对
，如果
满足如下可容许条件：
，其中为
的傅里叶变换，则可以称是一个基小波或母小波。
一个基小波的选择应满足以下两个条件：
- 是连续的且呈指数衰减(即
,对于某些常量C,M)。 
的积分为零(即
)。
由母小波进行伸缩和平移生成的函数系
，
其中，
，a是尺度参数，b是平移参数。
Morlet小波：
将小波变换应用到神经网络中，可以优化神经网络，从本质上改善其学习功能。虽然使用Sigmoid基函数的神经网络具有较强容错和函数逼近能力，但，Sigmoid函数的能量具有无限性，而待处理函数f为有限的
函数，也不能找到它与f对应的局部特性。而且Sigmoid函数需要无限多权值，网络规模难以确定。
特点：
- 小波基元及网络结构有可靠的理论依据。
- 全局极小解是唯一的。
- 函数学习能力逼近能力较强。
以BP神经网络拓扑结构为拘束，采用
小波函数作为隐层节点的激活函数，信号向前传播的同时误差反向传播。
S函数编写：
function [sys,x0,str,ts,simStateCompliance] = sfun_Wavelet(t,x,u,flag,T,j,xite,alfa)
switch flag,
case 0,
[sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes(T,j);
%初始化函数
case 3,
sys=mdlOutputs(t,x,u,xite,alfa);
%输出函数
case {1,2,4,9},
sys=[];
otherwise
DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes(T,j)
%调用初始化函数，T步长，j隐含层神经元数
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 4;
%定义输出变量，包括控制变量u,三个PID参数：Kp,Ki,Kd
sizes.NumInputs = 7;
%定义输入变量，包括7个参数[e(k);e(k-1);e(k-2);y(k);y(k-1);r(k);1]
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [];
str = [];
ts = [T 0];
global wi_2 wi_1 wo_2 wo_1 a_2 a_1 b_2 b_1 u_1
wi_2 =rand(j,4).*2-1;
%隐含层（k-2)权值系数矩阵，维数j*4，范围【-1，1】
wo_2 = rand(3,j);
%输出层（k-2）权值系数矩阵，维数3*j，范围【0，1】
wi_1 = wi_2;
%隐含层（k-1)权值系数矩阵，维数j*4
wo_1 = wo_2;
%输出层（k-1）权值系数矩阵，维数3*j
a_2=1000*ones(1,j);b_2=100*ones(1,j);
a_1=a_2;b_1=b_2;
%小波参数a,b，维度1*j
u_1=0;
simStateCompliance = 'UnknownSimState';
function sys=mdlOutputs(~,~,u,xite,alfa)
%调用输出函数
M=[2;5;15];
%PID权值
global wi_2 wi_1 wo_2 wo_1 a_2 a_1 b_2 b_1 u_1
xi = [u(6),u(4),u(1),u(7)];
%神经网络的输入xi=[u(6),u(4),u(1),u(7)]=[r(k),y(k),e(k),1] 维数1*4
xx = [u(1)-u(2);u(1);u(1)+u(3)-2*u(2)];
%xx=[u(1)-u(2);u(1);u(1)+u(3)-2*u(2)]=[e(k)-e(k-1);e(k);e(k)+e(k-2)-2*e(k-1)],3*1
I = xi*wi_1';
%计算隐含层的输入，I=神经网络的输入*隐含层权值系数矩阵的转置wi_1' 1*j
I=(I-b_1)./a_1;
Oh = (a_1.^(-1/2)).*cos(1.75*I).*exp(-(I.^2)/2);
%激活函数，计算隐含层的输出,为1*j的矩阵
O = wo_1*Oh';
%计算输出层的输入，维数3*1
K =exp(O)./(exp(O)+exp(-O));
%激活函数,计算输出层的输出K=[Kp,Ki,Kd]，维数为3*1
K=K.*M;
KIL=K(2)*xx(2);
if KIL>30
KIL=30;
end
if KIL<-30
KIL=-30;
end
uu=K(1)*xx(1)+KIL+K(3)*xx(3);
%计算控制变量u(k) 1*1
dyu = sign((u(4)-u(5))./(uu-u_1+0.000001));
%计算输出层加权系数修正公式的sgn
%sign((y(k)-y(k-1))/(u(k)-u(k-1)+0.000001）)近似代表偏导 维数1*1
dO = 2./(exp(O)+exp(-O)).^2;
%激活函数，维数3*1
delta3 = u(1)*dyu*xx.*dO;
wo = wo_1+xite*delta3*Oh+alfa*(wo_1-wo_2);
%输出层加权系数矩阵的修正
dI = (a_1.^(-3/2)).*(-1.75*sin(1.75*I).*exp(-(I.^2)/2)-I.*cos(1.75*I).*exp(-(I.^2)/2));
%激活函数，维数1*j
A=[a_1;a_1;a_1;a_1];
wi = wi_1+xite*(dI.*(delta3'*wo))'*xi./(A')+alfa*(wi_1-wi_2);
%隐含层加权系数修正
a=a_1+xite*dI.*I.*(delta3'*wo)+alfa*(a_1-a_2);
b=b_1+xite*dI.*(delta3'*wo)./a_1+alfa*(b_1-b_2);
%隐含层参数修正
wi_2=wi_1;
wi_1=wi;
wo_2=wo_1;
wo_1=wo;
a_2=a_1;
a_1=a;
b_2=b_1;
b_1=b;
u_1=uu;
%更新
sys = [uu;K(:)];
%输出层输出sys=[uu;Kp;Ki;Kd]在matlab/simulink中建立电机模型：
采用Id=0的控制方式：
WNN模块为：
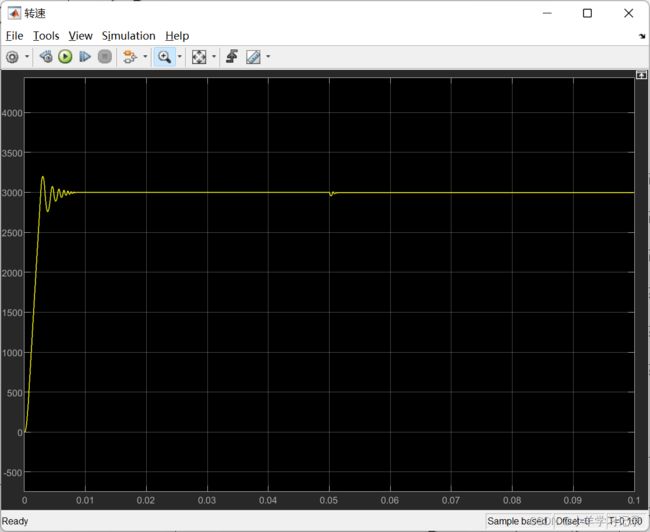
得到的转速图为：
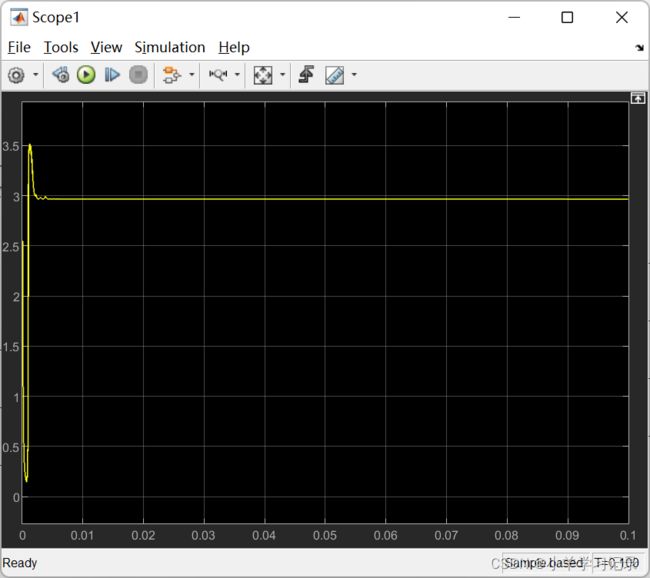
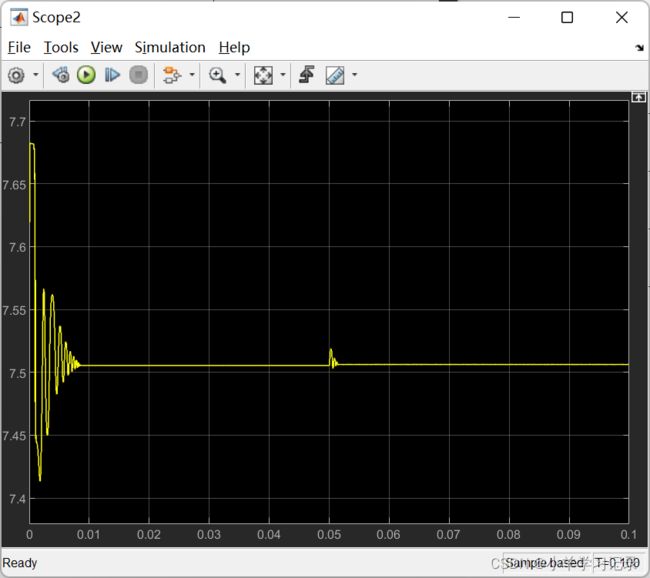
PID三个参数分别为：
其中BP神经网络的建模详见上一篇文章。
参考文献：
[1]霍召晗,许鸣珠.基于小波神经网络PID的永磁同步电机转速控制[J].电机与控制应用,2019,46(11):1-6.
[2]杜雪. 小波神经网络研究及其在PID控制器参数整定中的应用[D].哈尔滨工程大学,2016.
[3]J. Liu, M. Zhao, G. Li and J. Chen, "Multiple Linear Regression Prediction and Wavelet Neural Network Based Intelligent Online Tuning Control Method," in IEEE Access, vol. 8, pp. 160684-160696, 2020, doi: 10.1109/ACCESS.2020.3020980.