【动手学深度学习v2李沐】学习笔记05：多层感知机、详细代码实现

前文回顾：Softmax回归、损失函数、图片分类数据集、详细代码实现

一、感知机

1.1 单层感知机

给定输入$x$，权重$w$和偏移$b$，感知机输出：
$$o=\sigma (⟨w,x⟩+b)\sigma (x)=\{\begin{array}{l}1x>0\\ 0otherwise\end{array}$$

单层感知机实际是个二分类的问题，返回-1或者是1。

1.2 训练感知机

训练感知机的伪代码：

initialize $w=0$ and $b=0$
repeat
\qquad if $y_i[⟨w,x_i⟩+b]\le 0$ then
\qquad $w\leftarrow w+y_i{x}_i$ and $b\leftarrow b+y_i$
\qquad end if
until all classified correctly

上述伪代码中的 $y_i[⟨w,x_i⟩+b]\le 0$ ，是在判断真实值与预测值的乘积是否为正数：若为正数，说明预测正确；若为负数，说明预测错误，需要修改参数。这里实际上是个同或问题。感知机会不断进行这样的判断，并且不断地更新参数，直至对所有的类别均预测正确。
这段伪代码等价于使用批量大小为1的梯度下降，并使用如下的损失函数：
$$l(y,x,w)=max(0,-y⟨w,x⟩)$$

1.3 收敛定理

• 我们假设所有数据都在半径 $r$ 内
• 假设可以用余量 $\rho$ 将所有的数据分类成两类
  $$y(x^{T}w+b)\ge \rho$$对于$||w|{|}^2+b^2\le 1$
• 感知机保证在 $\frac{r^2+1}{{\rho }^2}$ 步后收敛。

1.4 XOR问题

感知机不能拟合XOR函数，它只能产生线性分割面。
由于感知机是一个线性模型，当两个不同类别的数据分布呈现异或的特征时，感知机无法对其进行分类。

1.5 总结

• 感知机是一个二分类问题，是最早的AI模型之一。
• 它的求解算法等价于使用批量大小为1的梯度下降。
• 它不能拟合XOR函数，导致第一次AI寒冬。

二、多层感知机

2.1 解决XOR问题

我们可以通过分多步来解决XOR问题，如下例所示。

• 首先，我们通过对x是否大于0训练绿色的线。
• 之后再通过对y是否大于0来训练红色的线。
• 最后，我们对两次训练的结果进行同或运算。
  

步骤\点	1	2	3	4
绿色线	+	-	+	-
红色线	+	+	-	-
同或	+	-	-	+

有了绿色分类器和红色分类器，我们就可以解决XOR问题了。上例中的分类器可以表示为由绿色分类器、红色分类器和同或分类器构成的多层分类器：

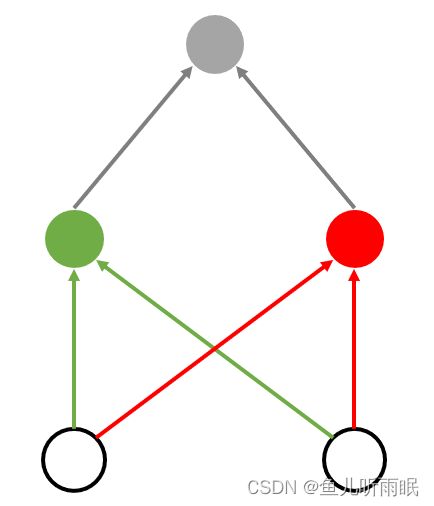
2.2 激活函数

2.2.1 Sigmoid激活函数

Sigmoid函数会将输入投影到 $(0,1)$ 区间之中，它可以看做是软的$\sigma (x)=\{\begin{array}{l}1x>0\\ 0otherwise\end{array}$
$$sigmiod(x)=\frac{1}{1+e^{-x}}$$

2.2.2 Tanh激活函数

这个函数和Sigmoid函数很像，区别是Tanh函数将输入投影到 $(-1,1)$ 区间中：
$$tanh(x)=\frac{1-e^{-2x}}{1+e^{-2x}}$$

2.2.3 ReLU激活函数

ReLU激活函数是个很常用的函数：
$$ReLU(x)=\max (x,0)$$

2.3 单隐藏层

多层感知机相当于加入了一个隐藏层的网络，隐藏层大小是超参数。

2.3.1 单分类问题

对于单分类问题，多层感知机的网络模型如下：

• 输入：$x\in R^n$
• 隐藏层：$W_1\in R^{m\times n},b_1\in R^m$
• 输出层：$w_2\in R^m,b_2\in R$

该模型相当于输入 $x$ 经过线性变换与激活函数 $\sigma ()$ 转变为隐藏层的 $h$。之后，又经过一个线性变换从输出层输出。
$$\begin{gathered} h=\sigma (W_{1}x+b_1) \\ o=w_2^{T}h+b_2 \end{gathered}$$这里，$\sigma$ 是按元素的激活函数。

问题： 为什么需要非线性激活函数？

---

我们假设激活函数为线性函数：$\sigma (x)=x$
网络模型变为：
$$\begin{gathered} h=W_{1}x+b_1 \\ o=w_2^{T}h+b_2 \end{gathered}$$ 则输出将会变为：$o=w_2^T{W}_{1}x+b^{\prime }$
此时，输出 $o$ 仍然为线性函数，模型仍然是个线性模型。该感知机仍然等于单层感知机。

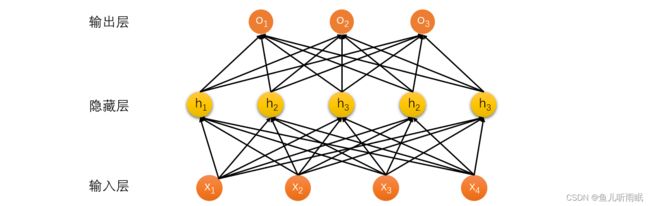
2.3.2 多分类问题

多层感知机解决多类分类问题相当于在Softmax回归的基础上，增加了一层隐藏层。
网络模型如下：

• 输入：$x\in R^n$
• 隐藏层：$W_1\in R^{m\times n},b_1\in R^m$
• 输出层：$W_2\in R^{m\times k},b_2\in R^k$

$$\begin{gathered} h=\sigma (W_{1}x+b_1) \\ o=W_2^{T}h+b_2 \\ y=\mathrm{softmax}(o) \end{gathered}$$

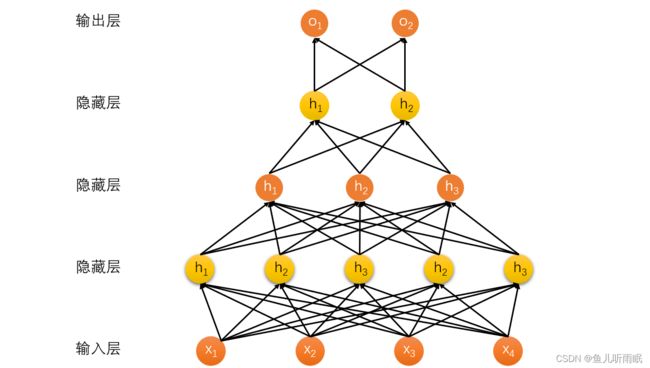
2.4 多隐藏层

我们在单隐藏层模型的基础上可以构造多隐藏层模型。例如：
$$\begin{gathered} h_1=\sigma (W_{1}x+b_1) \\ {h}_2=\sigma (W_2{h}_1+b_2) \\ {h}_3=\sigma (W_3{h}_2+b_3) \\ o=W_4{h}_3+b_4 \end{gathered}$$多隐藏层的每一层都有一个激活函数 $\sigma ()$ 和一个偏移 $b_i$
多隐藏层的超参数有：

• 隐藏层数
• 每层隐藏层的大小

输入数据的复杂度应当和模型的复杂度相匹配。如果输入数据比较复杂，我们有两个选择：

1. 采用单隐藏层，并且设置比较大的隐藏层大小。
2. 采用多隐藏层，采用较小的隐藏层大小以及更深层次的网络。

2.5 总结

• 多层感知机使用隐藏层和激活函数来得到非线性模型。
• 常用激活函数是Sigmoid、Tanh和ReLU。
• 使用Softmax来处理多类分类问题。
• 超参数为隐藏层数和各隐藏层大小。

三、代码实现

3.1 从零开始实现

3.1.1 导入库和加载数据集

import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

3.1.2 单隐藏层多层感知机

我们实现一个具有单隐藏层的多层感知机，它处理的输入数据大小为784，输出为10个类别，包含256个隐藏单元。我们将每一层的权重随机初始化，并将偏移初始化为0。

# 实现一个多层感知机
# 输入 输出 隐藏层
num_inputs, num_outputs, num_hiddens = 784, 10, 256

W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True))
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True))
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))

params = [W1, b1, W2, b2]

3.1.3 激活函数

我们实现ReLU激活函数

# 实现ReLU激活函数
def relu(X):
    a = torch.zeros_like(X)
    return torch.max(X, a)

3.1.4 模型和损失函数

实现我们的模型以及损失函数

# 实现我们的模型
def net(X):
    X = X.reshape((-1, num_inputs))
    H = relu(X @ W1 + b1)   # 这里的@是矩阵乘法，相当于matmul()
    return (H @ W2 + b2)

# 损失函数
loss = nn.CrossEntropyLoss(reduction='none')

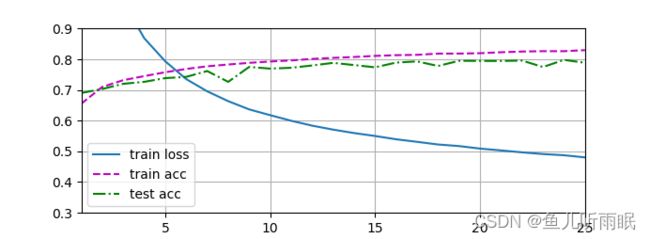
3.1.5 训练

多层感知机的训练过程与softmax回归的训练过程完全相同。

# 训练过程
num_epochs, lr = 25, 0.2
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)

训练结果如下图所示：

3.2 简洁实现

3.2.1 导入库

import torch
from torch import nn
from d2l import torch as d2l

3.2.2 模型

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net = nn.Sequential(nn.Flatten(),
                    nn.Linear(784, 256),
                    nn.ReLU(),
                    nn.Linear(256, 10))
net.apply(init_weights)

3.2.3 训练

# 训练过程
batch_size, lr, nums_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=lr)

train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, nums_epochs, updater=trainer)

训练的结果如下图所示：

下一篇：【动手学深度学习v2李沐】学习笔记06：模型选择、欠拟合和过拟合、代码实现