SLAM传感器篇:深度相机
深度相机,指可获取场景中物体与摄像头之间物理距离的相机。主流深度相机通常由多种镜头、光学传感器组成,根据基本原理可以分为:飞行时间法、结构光法、双目立体视觉法。
相机成像模型
在研究深度相机之前,先来分析一下相机成像的模型:
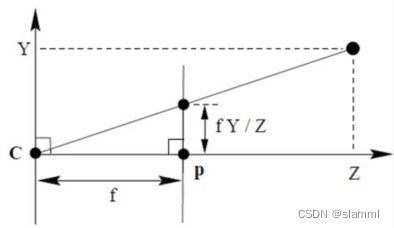
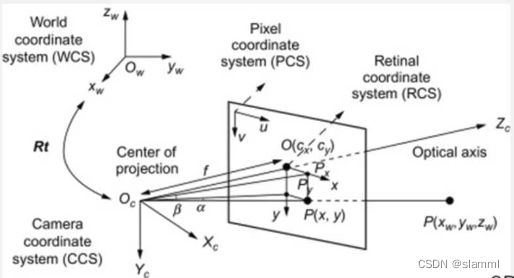
坐标系:世界坐标系( X , Y X,Y X,Y)、相机坐标系( x , y x,y x,y)、归一化平面( z = 1 z=1 z=1)坐标系( x ′ , y ′ x',y' x′,y′)、像素平面坐标系( u , v u,v u,v)。
根据外参坐标变换( R , t R,t R,t),可得:
[ x y z ] = [ 1 0 0 0 0 1 0 0 0 0 1 0 ] ∗ [ X Y Z 1 ] \begin{bmatrix}x \\y \\z\end{bmatrix}=\begin{bmatrix}1 & 0 & 0 & 0 \\0 & 1 & 0 & 0 \\0 & 0 & 1 & 0 \\\end{bmatrix}*\begin{bmatrix}X \\Y \\Z \\1\end{bmatrix} ⎣ ⎡xyz⎦ ⎤=⎣ ⎡100010001000⎦ ⎤∗⎣ ⎡XYZ1⎦ ⎤
根据三角形相似,可得:
y ′ / y = x ′ / x = f / z y'/y=x'/x=f/z y′/y=x′/x=f/z
根据成像关系,可得:
u = s x ∗ x ′ + c x ; v = s y ∗ v + c y ; s x , s y 均为尺度因子 ( p i x / m ) u=s_x*x'+c_x;v=s_y*v+c_y;s_x,s_y均为尺度因子(pix/m) u=sx∗x′+cx;v=sy∗v+cy;sx,sy均为尺度因子(pix/m)
u = ( f x ∗ x ) / z + c x ; v = f y ∗ y / z + c y u=(f_x*x)/z+c_x;v=f_y*y/z+c_y u=(fx∗x)/z+cx;v=fy∗y/z+cy
使用齐次坐标,可得:
z [ u v 1 ] = [ f x 0 c x 0 f y c y 0 0 1 ] ∗ [ 1 0 0 0 0 1 0 0 0 0 1 0 ] ∗ [ X Y Z 1 ] z\begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} * \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} * \begin{bmatrix} X \\ Y \\ Z \\ 1 \end{bmatrix} z⎣ ⎡uv1⎦ ⎤=⎣ ⎡fx000fy0cxcy1⎦ ⎤∗⎣ ⎡100010001000⎦ ⎤∗⎣ ⎡XYZ1⎦ ⎤
到此,通过外参、内参建立起世界到像素的映射关系。
飞行时间法(Time of Flight,TOF)
飞行时间法,测距原理是通过连续发射光脉冲到观测物体,接收从观测物体返回的光脉冲,通过计算光脉冲的飞行(往返)时间获取观测物体与相机之间的距离。
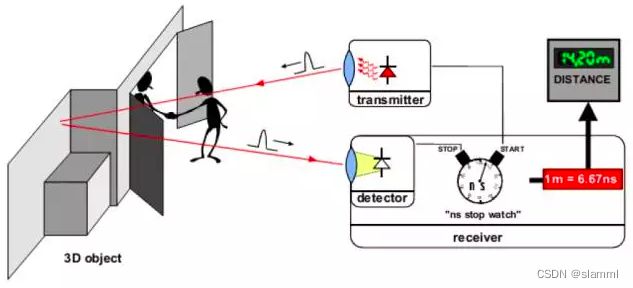
优点:
1.测量误差在测量范围基本固定;
2.抗干扰能力强;
3.测量距离较远时具有明显优势;
缺点:
1.对时间测量精度要求高,采用最高精度电子元器件,也很难达到毫米级精度;
结构光法
结构光法,使用提前设计好的特殊结构图案(比如离散光斑、条纹光、编码结构光等)投影到观测物体表面,使用另一个相机观察图案在物体表面成像的畸变情况,根据已知图案与变形使用算法计算观测物体的三维形状、深度。
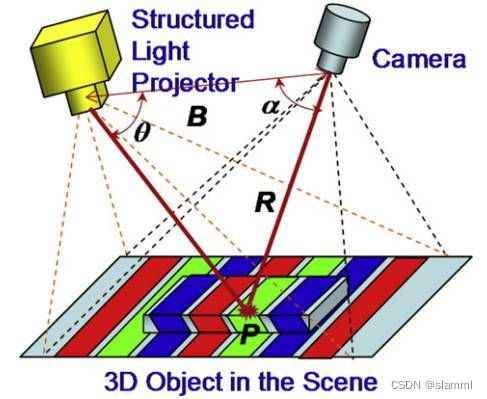
优点:
1.精度高;
2.不依赖光照条件;
缺点:
1.物理器件复杂,体积较大;
2.不适合室外环境,编码光容易被自然光影响;
3.容易导致测量失败的物体:深色(尤其黑色)物体(深色物体对红外光的吸收能力强)、一定光滑程度的物体、透明物体(红外光可以产生透射现象)
4.物体边缘存在视觉盲区(发射端、接收端有一定间距)
双目立体视觉法
双目立体视觉,类比人眼,通过计算同一物体在两个相机成像的视差根据三角关系得到物体与相机之间的距离。

根据相似三角形原理,已知焦距 f f f、基线 b b b,只要求得视差 d = x l − x r d=x_l-x_r d=xl−xr(像素平面),便可以得出深度。那么视差该怎么求解呢?假设两相机共面且光轴平行、参数相同,借助极线约束匹配点在两相机中成像的点,便可以求得视差。那么极线约束又是什么呢?首先定义一下极线,空间中点与两相机中心构成的平面与左右图像平面的交线就是极线;再来看下极线约束,同一空间点成像,已知左图成像点,那么右图成像点一定在相对于左图成像点的极线上,以此缩短匹配范围。
介绍完基于理想假设下的基本原理,再说一下非理想情况该怎么处理。通过图像矫正转换到理想假设,即将不同方向的图像平面重新投影到同一平面且光轴平行,那具体怎么操作呢?可以对两张图片使用相机标定得到的单应矩阵变换得到矫正后的图像,此时相机极线也变成水平了。
在实际操作中,会存在一些问题:
1.保证相机共面且参数一致很难,计算过程中也会存在误差累积,对于左图点在右图中对应的点可能在极线附近,搜索范围应适当放宽;
2.单像素点鲁棒性很差,容易受到光照和视角影响;

目前有两种主流的解决方法,滑动窗口法、能量优化法。滑动窗口法是使用固定尺寸的滑动窗口计算相似度(像素差)进行匹配,但是匹配效果不好且计算效率低;能量优化法是通过设定能量函数进行优化得到,该方法目前使用较多。
深度测量过程:

1.标定双目相机,获得两个相机的内外参、单应矩阵;
2.使用单应矩阵校正图像,使得左右两张图位于同一平面且平行;
3.根据极线约束匹配像素点,得到匹配结果计算像素深度。
优点:
1.硬件要求低,成本低,不需TOF与结构光使用特殊的发射器和接收器;
2.室内外均适用,相比之下,TOF和结构光基本只能在室内使用;
缺点:
1.对光照条件敏感,亮度差异会导致成像差异;
2.不适合纹理缺失的场景;
3.需要逐像素运算,计算复杂度高;
4.基线限制了测量范围;

Stereolabs ZED 是基于RGB双目立体视觉原理的深度相机,室内和室外都能使用,最远深度范围可达20m,深度图分辨率最高达 4416x1242 @ 15FPS,可以根据帧率需要调整,最高帧率1344x376 @ 100FPS,最大覆盖视场角为110°。
下面表格是对上述三种深度相机关键特性的对比:
| 时间飞行法 | 结构光法 | 立体双目视觉法 | |
|---|---|---|---|
| 测量精度 | 厘米级 | 0.01mm-1mm(近距离) | 毫米级 |
| 测量范围 | 100米以内 | 10米以内 | 2米以内(基线10mm) |
| 帧率 | 上百fps | 30fps | - |
| 分辨率 | 低于640x480 | 1080x720 | 2K |
参考资料:
[1]. 深度相机原理揭秘–双目立体视觉
[2]. 聊聊三维重建-双目立体视觉原理
[3]. ZED Stereo Camera Stereolabs