从EM算法到高斯混合模型（GMM）与K-means算法（理论分析+仿真分析）

目录：

• EM算法
• GMM模型
• K-means算法

EM算法

基本问题

  首先介绍一下EM算法要解决的基本问题。EM算法通常解决的是不同分布下的参数估计问题，属于参数估计理论的一种。在另一个角度，EM算法也可以看作是极大似然估计的加强版。

  由于极大似然估计要求采样数据属于同一个分布，因为只能估计同一个分布下的参数。
  举个例子：在学校随机地选取100个男生，可以通过极大似然估计来得到男生的平均身高。倘若随机选取100个未知性别的学生（有男有女），这时，这100个人的平均身高既不代表男生也不代表女生。

  此时，正确地做法应该是先把女生和男生分开，然后分别用极大似然估计，最后分别得到了男生和女生的平均身高。

数学描述

  若样本$X=\{X_1,X_2....X_n\}$，一共有$N$个不同的样本，其中样本$X_i$属于$K(k=1,2...K)$个不同的分布。即$X_i\sim p(x|{\theta }_k)$，$X_i$是从第$k$个分布里面抽取出来的样本。现在的问题是需要得到$p(x|{\theta }_k)$。下面就是EM算法要解决的问题了，做法很简单，思想确实很精巧。

1.极大似然估计

  EM算法还是从极大似然出发的，前面说过，这玩意就是极大似然的加强版本。首先写出样本$X=\{X_1,X_2....X_n\}$的似然函数:

$$L(\theta )=\prod _{i=1}^{N}p(x_i|{\theta }_k)\text{\hspace{1em}(1)}$$
  观察$(1)$式子可以看出似然函数中含有${\theta }_k$,$k$是未知的，所以这里引入一个叫隐变量的东西。首先隐变量有几个特点（个人理解）：

• 隐变量是一个随机变量
• 每个样本$X_i$都对应一个隐变量值$Z_j$，但是不意味隐变量可以取$N$个值，同一分布内（同一类）的样本对应隐变量的值是一样的。
• 隐变量描述的是$X_i$归属于哪个分布的现象。

  主要解释一下后面两点，想想最开始提到的100个学生，其实每个学生我们不仅仅能测量他的身高，我们还应该知道他的性别。所以，完整地描述一个人的身高应该是$(X_i,Z_j)$，前者表示升高，后者表示性别。

  利用隐变量，对$(1)$式进行改写：

$$L(\theta )=\prod _{i=1}^N\sum _{k=1}^{K}p(x_i|{\theta }_k)\text{\hspace{1em}(2)}$$

  这里的解释是既然不知道每个样本$X_i$所对应的分布$p(x|{\theta }_k)$，那么干脆下面主要处理

$$X_i\sim \sum _{k=1}^{K}p(x_i|{\theta }_k)$$

  这个其实是代表这每个分布都对$X_i$有贡献，只是大小不一样，那么就直接求和取最大就好了。

  对$(2)$式取对数，有：

$$log[L(\theta )]=\sum _{i=1}^{N}log\sum _{k=1}^{K}p(x_i|{\theta }_k)\text{\hspace{1em}(3)}$$

  按照极大似然的做法，接下来要对$(3)$式求导了，由于对数内求和再求导，将会无比复杂，所以不能求导。这里需要用到一个不等式。

2.琴声不等式

  对于一个凹函数有以下不等式成立：

$$f(E(x))\ge E(f(x))$$

  如果$x$是离散的随机变量，那么有：

$$f(\sum xp(x))\ge \sum f(x)p(x)$$

  前面提到，每个样本$Z_i$对于一个隐变量的取值$Z_j$,设隐变量$Z_j$对应的概率密度值为$Q(Z_j)$，$(3)$式可写成如下形式：

$$log[L(\theta )]=\sum _{i=1}^{N}log\sum _{k=1}^{K}Q(Z_j)\frac{p(x_i|{\theta }_k)}{Q(Z_j)}\text{\hspace{1em}(4)}$$

对$(4)$应用琴声不等式。

$$f--->log$$

$$x--->\frac{p(x_i|{\theta }_k)}{Q(Z_j)}$$

$$p(x)--->Q(Z_j)$$

  所以有：

$$\sum _{i=1}^{N}log\sum _{k=1}^{K}Q(Z_j)\frac{p(x_i|{\theta }_k)}{Q(Z_j)}\ge \sum _{i=1}^N\sum _{k=1}^{K}log(\frac{p(x_i|{\theta }_k)}{Q(Z_j)})Q(Z_j)=J(Z,\theta )\text{\hspace{1em}(5)}$$

  由$(5)$式可以看出$logL(\theta )\ge J(Z,\theta )$，显然$J(Z,\theta )$是似然函数的下界，只要不断提高$J(Z,\theta )$，就能不断提高$logL(\theta )$。这里有个问题：

• 如何提高$J(Z,\theta )$？？？

$$J(Z,\theta )=\sum _{i=1}^N\sum _{k=1}^{K}log(\frac{p(x_i|{\theta }_k)}{Q(Z_j)})Q(Z_j)$$

  显然需要把$Q(z_j)$先求出来（EM算法的E步），然后求导估计${\theta }_k$(EM算法的M步)。

3.E步

  因为$Z$是隐变量，也是一个随机变量，所以有:

$$\sum _{z}Q(Z_j)=1$$

  当琴声不等式取"="号时，有：

$$\frac{p(x_i|{\theta }_k)}{Q(Z_j)}=c=\frac{{\sum }_{k=1}^{K}p(x_i|{\theta }_k)}{{\sum }_{z}Q(Z_j)}=\sum _{k=1}^{K}p(x_i|{\theta }_k)$$

  所以$$Q(Z_j)=\frac{p(x_i|{\theta }_k)}{{\sum }_{k=1}^{K}p(x_i|{\theta }_k)}$$

  从这里可以看出，如果$p(x_i|{\theta }_k)=p(x_{i+1}|{\theta }_k)$,那么$Q(Z_j)=Q(Z_{j+1})$。即对于同分布的样本，其隐变量取值相同的概率是一样的。

  通过初始化${\theta }_k$，那么就可先估计出$Q(Z_j)$。这是E步。

4.M步

  当$Q(Z_j)$已知，带入$J(Z,\theta )$，令$\frac{dJ(z,\theta )}{d\theta }=0$，估计$\theta$。

  重复E步与M步，直到算法收敛，这就是EM算法啦~

高斯混合模型（GMM）

  高斯混合模型是利用多个高斯分布对任意的分布进行拟合。最大的问题也是参数估计，用的方法也是EM算法。

1.极大似然估计

  设有样本$X=\{X_1,X_2....X_n\}$，对样本$X_i$

$$X_i\sim \sum _{k=1}^K{\pi }_{k}N({\mu }_k,{\Sigma }_k)$$

  即利用$K$个高斯分布进行拟合。
  对于样本$X_i$引入$K$维隐变量$Z_j=\left[\begin{array}{c}{z}_{j1}\\ z_{j2}\\ ⋮\\ z_{jk}\end{array}\right]$，其中${\sum }_{k=1}^K{z}_{jk}=1$，且只有一个分量能等于$1$，代表该高斯分量的概率最大。

  下面要混合高斯分布写成包含隐变量的形式，需要用到概率公式。
  对于$Q(z_{jk})$

$$Q(z_{jk})={\pi }_k,z_{jk}=1$$

$$Q(z_{jk})=1,z_{jk}=0$$

所以$$Q(z_{jk})={\pi }_k^{z_{jk}}\text{\hspace{1em}(6)}$$

对于$p(X_i,Z_j)$有：

$$p(X_i,Z_j)=\prod _{k=1}^{K}p(X_i|z_{jk})Q(z_{jk})\text{\hspace{1em}(7)}$$

$(7)$式用到了全概率公式，且：
$$p(X_i|z_{jk})=N(X_i|{\mu }_k,{\Sigma }_k{)}^{z_{jk}}\text{\hspace{1em}(8)}$$

把$(6)(7)$代入$(8)$,带隐变量的GMM分布为：

$$p(X_i,Z_j)=\prod _{k=1}^{K}N(X_i|{\mu }_k,{\Sigma }_k{)}^{z_{jk}}{\pi }_k^{z_{jk}}\text{\hspace{1em}(9)}$$

带隐变量的似然函数为：

$$L(X,Z,\mu ,\Sigma )=\prod _{i=1}^N\prod _{k=1}^{K}N(X_i|{\mu }_k,{\Sigma }_k{)}^{z_{jk}}{\pi }_k^{z_{jk}}\text{\hspace{1em}(10)}$$

取对数得：
$$ln(L(X,Z,\mu ,\Sigma ))=\sum _{k=1}^K(\sum _{j=1}^N{z}_{jk})ln({\pi }_k)+\sum _{i=1}^N{z}_{jk}ln(N(X_i|{\mu }_k,{\Sigma }_k))\text{\hspace{1em}(11)}$$

2.E步

  估计$Z_j$,根据EM算法的E步有：

$$E(Z_j)=Q(Z_j)Z_j=\frac{{\pi }_{k}N(X_i)}{{\sum }_{k=1}^k{\pi }_{k}N(X_i)}$$

  其中，$E(Z_j)$是一个$K$维的向量。这个式子可以直接根据EM算法导出，也可以根据概率公式进行计算。

2.M步

  有了E步，即知道了$Z_j$，那么可以直接对$(11)$式子求导了，具体的求导运算不写了，直接给结果吧。

$${\mu }_k=\frac{{\sum }_{i=1}^N{z}_{jk}{X}_i}{{\sum }_{i=1}^N{z}_{jk}}$$

$${\Sigma }_k=\frac{{\sum }_{i=1}^N{z}_{jk}(X_i-{\mu }_k{)}^T(X_i-{\mu }_k)}{{\sum }_{i=1}^N{z}_{jk}}$$

$${\pi }_k=\frac{{\sum }_{i=1}^N{z}_{jk}}{N}$$

3.matlab仿真

clear;%%以下用GMM模型进行聚类

%首先产生数据,%%产生了80个数据点，均服从二维高斯分布
X1=normrnd(3,1,[100 2]);
X2=normrnd(6,1.5,[40 2]);
X=[X1',X2'];  

%初始化相应的参数；
N=length(X);
beta=0.001;%正则化因子
% Pai=0.5*ones(2,1);%%这是混合GMM的分量
Pai(1)=0.2;Pai(2)=0.8;

mu_1=rand(1)*ones(2,1);%产生均值矩阵
mu_2=rand(1)*ones(2,1); 

Var_1=rand(1)*eye(2);%产生协方差矩阵
Var_2=rand(1)*eye(2); 

for iter=1:20
    
    
%E步
    for i=1:N
        
    N_x_1=mvnpdf(X(:,i),mu_1,Var_1);%对应概率密度的值
    N_x_2=mvnpdf(X(:,i),mu_2,Var_2);
    
    EZ(1,i)=Pai(1)*N_x_1/(Pai(1)*N_x_1+Pai(2)*N_x_2); %估计隐变量   
    EZ(2,i)=Pai(2)*N_x_2/(Pai(1)*N_x_1+Pai(2)*N_x_2); 
      
    end
   
%M步

%1)更新均值向量    
N_k1=sum(EZ(1,:));
N_k2=sum(EZ(2,:)); %隐变量对于分量的和
m1=0;m2=0;
    for i=1:N  
        m1=m1+EZ(1,i)*X(:,i); 
        
        m2=m2+EZ(2,i)*X(:,i); 
    end   
mu_1=m1/N_k1;
mu_2=m2/N_k2; 

%2)更新协方差矩阵

V1=0;V2=0; %代表临时的方差矩阵

    for i=1:N         
    V1=V1+EZ(1,i)*(X(:,i)-mu_1)*(X(:,i)-mu_1)';
    V2=V2+EZ(2,i)*(X(:,i)-mu_2)*(X(:,i)-mu_2)'; %%更新方差矩阵               
    end
    
    Var_1=V1/N_k1+beta*eye(2);
    Var_2=V2/N_k2+beta*eye(2); 
    
%3)更新pai值
Pai(1)=N_k1/N;
Pai(2)=N_k2/N;

    
    
end
    


%%看看效果
for i=1:N
    if(EZ(1,i)>=EZ(2,i))
        rx1(:,i)=X(:,i);
    else
        rx2(:,i)=X(:,i);
    end
end


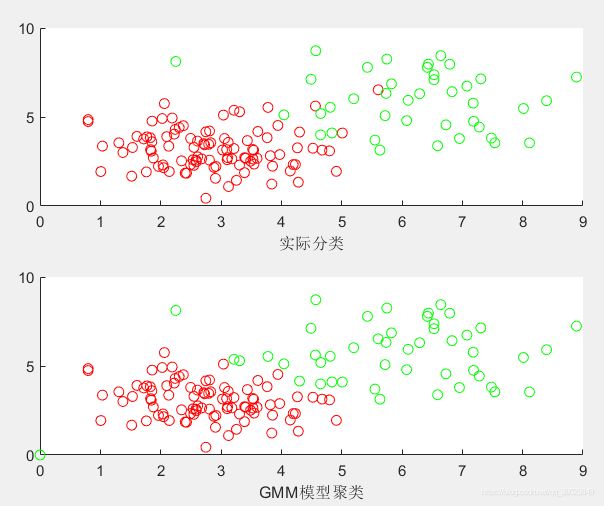
subplot(2,1,1);
scatter(X1(:,1),X1(:,2),'r');
hold on;
scatter(X2(:,1),X2(:,2),'g');
xlabel('实际分类');
hold off;


subplot(2,1,2);
scatter(rx1(1,:),rx1(2,:),'r');
hold on;
scatter(rx2(1,:),rx2(2,:),'g');
xlabel('GMM模型聚类')
hold off;

结果：

K-means算法

  K-means只是GMM模型的退化，弄明白了EM和GMM算法，K-means很容易理解。

1.理论分析

  目标函数如下：

$$J=\sum _{i=1}^N\sum _{k=1}^K||(X_i-{\mu }_k)||$$

  E步，经过初始后，先大概分类：
$$d_k=||X_i-{\mu }_k||$$
  对于$X_i$，$d_k$最大，则划分为第$k$类，这个过程也可以用GMM模型中的隐变量表示。

  M步，估计${\mu }_k$

$${\mu }_k=\frac{{\sum }_{k=1}^{N_k}{X}_k}{N_k}$$
  表达了对所以的$k$类数据求取均值。

2.matlab仿真

clear;%%以下用K-means模型进行聚类

%首先产生数据,%%产生了80个数据点，均服从二维高斯分布
X1=normrnd(3,1,[100 2]);
X2=normrnd(6,1.5,[100 2]);
X=[X1',X2'];  

%初始化相应的参数；
N=length(X);
iter=20;
x1_=[0,2]';
x2_=[3,3]'; %均值（质心的初始值）

for j=1:iter
    %E步
    for i=1:N
    d_1=norm(X(:,i)-x1_);
    d_2=norm(X(:,i)-x2_);
    if(d_1<d_2)
        z(:,i)=[1;0];
    else
        z(:,i)=[0;1];
    end
    
    end


%M步
%分别计算更新后的x1_,x2_
tmp_1=0;tmp_2=0;
N_1=0;N_2=0;
    for(i=1:N)
        if( z(:,i)==[1;0])
            tmp_1=tmp_1+X(:,i);
            N_1=N_1+1;
        else
            tmp_2=tmp_2+X(:,i);
            N_2=N_2+1;
        end

    end
x1_=tmp_1/N_1;
x2_=tmp_2/N_2;

%%看看误差
    e(j)=0;
    for(i=1:N)  
        e(j)=e(j)+norm(X(:,i)-x1_)+norm(X(:,i)-x2_);
    end
    
end

%画图

%%看看效果
for i=1:N
    if(z(:,i)==[1,0]')
        rx1(:,i)=X(:,i);
    else
        rx2(:,i)=X(:,i);
    end
end


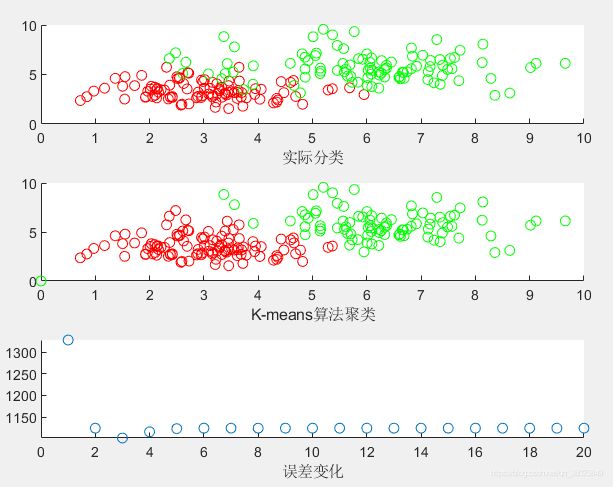
subplot(3,1,1);
scatter(X1(:,1),X1(:,2),'r');
hold on;
scatter(X2(:,1),X2(:,2),'g');
xlabel('实际分类');
hold off;


subplot(3,1,2);
scatter(rx1(1,:),rx1(2,:),'r');
hold on;
scatter(rx2(1,:),rx2(2,:),'g');
xlabel('K-means算法聚类');
hold off;
subplot(3,1,3)
m=1:1:iter;
scatter(m',e);
xlabel('误差变化');

最后要感谢几位大神的博客，受益匪浅！！
参考文献：
[1]https://blog.csdn.net/jinping_shi/article/details/59613054

[2]https://blog.csdn.net/lin_limin/article/details/81048411?utm_medium=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.add_param_isCf&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.add_param_isCf

[3]https://blog.csdn.net/zouxy09/article/details/8537620