神将网络(3)反向传播算法及推导
1.反向传播算法
在前一篇文章中我们介绍了神经网络的前向传播并构建出了损失函数。我们从输入层开始一层一层向前进行计算,一直到最后一层的 h θ ( x ) h_{\theta}(x) hθ(x)。现在为了计算使用梯度下降法就要计算偏导数 ∂ θ i , j ( l ) J ( θ ) \frac{\partial}{\theta^{(l)}_{i,j}}J(\theta) θi,j(l)∂J(θ),我们需要采用一种反向传播的算法,也就是先计算最后一层的误差,然后再一层一层反向求出各层的误差,直到倒数第二层(应为倒数第一层为输入层即x本身,不会存在误差)。
反向传播算法步骤:
1.对神经网络的权值进行随机初始化
2:遍历所有样本
1.运用前向传播算法,得到预测值 a L = h θ ( x ) a^{L}=h_{\theta}(x) aL=hθ(x).
&emps;2.运用反向传播算法,从输出层开始计算每层的误差,以此来求取偏导。输出层的误差即为预测值与真实值之间的差值: δ L = a L − y \delta^{L}=a^{L}-y δL=aL−y,对于隐藏层中的每一层的误差,都通过上一层的误差来计算。得到 δ l = ( θ ( l ) ) T δ l + 1 . ∗ a ( l ) ∗ ( 1 − a ( l ) , a 0 ( l ) = 1 \delta^{l}=(\theta^{(l)})^{T}\delta^{l+1}.*a^{(l)}*(1-a^{(l)},a^{(l)}_{0}=1 δl=(θ(l))Tδl+1.∗a(l)∗(1−a(l),a0(l)=1
依次求解并累加误差。 Δ i , j ( l ) = Δ i , j ( l ) + a j ( l ) δ i l + 1 \Delta^{(l)}_{i,j}=\Delta^{(l)}_{i,j}+a_{j}^{(l)}\delta^{l+1}_{i} Δi,j(l)=Δi,j(l)+aj(l)δil+1,向量化实现: Δ l = ∣ D e l a t a l + δ l + 1 ( a ( l ) ) T \Delta^{l}=|Delata^{l}+\delta^{l+1}(a^{(l)})^{T} Δl=∣Delatal+δl+1(a(l))T
3.遍历完所有样本后,求得偏导为: ∂ ∂ θ i , j ( l ) J ( θ ) = D i , j ( l ) \frac{\partial}{\partial \theta^{(l)}_{i,j}}J(\theta)=D^{(l)}_{i,j} ∂θi,j(l)∂J(θ)=Di,j(l)

2.反向传播算法推导

假设样本只有一个,则:
先令 δ ( l ) = ∂ ∂ z ( l ) J ( θ ) \delta^{(l)}=\frac{\partial}{\partial z^{(l)}}J(\theta) δ(l)=∂z(l)∂J(θ),
故
∂ ∂ θ ( 3 ) J ( θ ) = ∂ J ( θ ) ∂ z ( 4 ) ∂ z ( 4 ) ∂ θ ( 3 ) = δ ( 4 ) ∂ z ( 4 ) ∂ θ ( 3 ) \frac{\partial}{\partial{\theta^{(3)}}}J(\theta)=\frac{\partial{J(\theta)}}{\partial{z^{(4)}}}\frac{\partial{z^{(4)}}}{\partial{\theta^{(3)}}}=\delta^{(4)}\frac{\partial{z^{(4)}}}{\partial{\theta^{(3)}}} ∂θ(3)∂J(θ)=∂z(4)∂J(θ)∂θ(3)∂z(4)=δ(4)∂θ(3)∂z(4)
又因为 z ( 4 ) = θ ( 3 ) a ( 3 ) z^{(4)}=\theta^{(3)}a^{(3)} z(4)=θ(3)a(3),故 ∂ z ( 4 ) ∂ θ ( 3 ) \frac{\partial{z^{(4)}}}{\partial{\theta^{(3)}}} ∂θ(3)∂z(4)= a ( 3 ) a^{(3)} a(3),
故证得 ∂ ∂ θ ( 3 ) J ( θ ) = a ( 3 ) δ ( 4 ) \frac{\partial}{\partial{\theta^{(3)}}}J(\theta)=a^{(3)}\delta^{(4)} ∂θ(3)∂J(θ)=a(3)δ(4)
代价函数无正则项时其:
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) l o g ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) l o g ( 1 − ( h θ ( x ( i ) ) ) ) ] J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log(h_{\theta}(x^{(i)}))+(1-y^{(i)})log(1-(h_{\theta}(x^{(i)})))] J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−(hθ(x(i))))]
h θ ( x ) = a ( L ) = g ( z ( L ) ) h_{\theta}(x)=a^{(L)}=g(z^{(L)}) hθ(x)=a(L)=g(z(L)), g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1,带入到J中(为方便计算m=1)
J ( θ ) = − y l o g ( 1 1 + e − z ) − ( 1 − y ) l o g ( 1 − 1 1 + e − z ) J(\theta)=-ylog(\frac{1}{1+e^{-z}})-(1-y)log(1-\frac{1}{1+e^{-z}}) J(θ)=−ylog(1+e−z1)−(1−y)log(1−1+e−z1)
= y l o g ( 1 + e − z ) − ( 1 − y ) l o g ( e − z 1 + e − z ) =ylog(1+e^{-z})-(1-y)log(\frac{e^{-z}}{1+e^{-z}}) =ylog(1+e−z)−(1−y)log(1+e−ze−z)
= y l o g ( 1 + e − z ) + ( 1 − y ) l o g ( 1 + e z ) =ylog(1+e^{-z})+(1-y)log(1+e^{z}) =ylog(1+e−z)+(1−y)log(1+ez)
δ ( 4 ) = ∂ ∂ z ( 4 ) J ( θ ) = ∂ ∂ z ( 4 ) ( y l o g ( 1 + e − z ( 4 ) ) + ( 1 − y ) l o g ( 1 + e z ( 4 ) ) ) \delta^{(4)}=\frac{\partial}{\partial{z^{(4)}}}J(\theta)=\frac{\partial}{\partial{z^{(4)}}}(ylog(1+e^{-z^{(4)}})+(1-y)log(1+e^{z^{(4)}})) δ(4)=∂z(4)∂J(θ)=∂z(4)∂(ylog(1+e−z(4))+(1−y)log(1+ez(4)))
= y − e − z ( 4 ) 1 + e − z ( 4 ) + ( 1 − y ) e z ( 4 ) 1 + e z ( 4 ) =y\frac{-e^{-z^(4)}}{1+e^{-z^{(4)}}}+(1-y)\frac{e^{z^{(4)}}}{1+e^{z^{(4)}}} =y1+e−z(4)−e−z(4)+(1−y)1+ez(4)ez(4)
= − y e ( − z ( 4 ) ) − y e − z ( 4 ) e z ( 4 ) + 1 − y + e z ( 4 ) − y e ( z 4 ) ( 1 + e ( − z ( 4 ) ) ) ( 1 + e ( z ( 4 ) ) ) =\frac{-ye^{(-z^{(4)})}-ye^{-z^{(4)}}e^{z^{(4)}}+1-y+e^{z^{(4)}}-ye^{(z^{4})}}{(1+e^{(-z^{(4)})})(1+e^{(z^{(4)})})} =(1+e(−z(4)))(1+e(z(4)))−ye(−z(4))−ye−z(4)ez(4)+1−y+ez(4)−ye(z4)
= ( 1 − y ) e z ( 4 ) − ( 1 + e z ( 4 ) ) y e z − ( 4 ) + ( 1 − y ) ( 1 + e ( − z ( 4 ) ) ) ( 1 + e ( z ( 4 ) ) ) =\frac{(1-y)e^{z^{(4)}}-(1+e^{z^{(4)}})ye^{z^{-(4)}}+(1-y)}{(1+e^{(-z^{(4)})})(1+e^{(z^{(4)})})} =(1+e(−z(4)))(1+e(z(4)))(1−y)ez(4)−(1+ez(4))yez−(4)+(1−y)
= ( 1 − y ) ( 1 + e ( z ( 4 ) ) ) ) − ( 1 + e z ( 4 ) ) y e z − ( 4 ) ( 1 + e ( − z ( 4 ) ) ) ( 1 + e ( z ( 4 ) ) ) =\frac{(1-y)(1+e^{(z^{(4)})}))-(1+e^{z^{(4)}})ye^{z^{-(4)}}}{(1+e^{(-z^{(4)})})(1+e^{(z^{(4)})})} =(1+e(−z(4)))(1+e(z(4)))(1−y)(1+e(z(4))))−(1+ez(4))yez−(4)
= ( 1 − y − y e − z ( 4 ) ) ( 1 + e ( z ( 4 ) ) ) ( 1 + e ( − z ( 4 ) ) ) ( 1 + e ( z ( 4 ) ) ) =\frac{(1-y-ye^{-z^{(4)}})(1+e^{(z^{(4)})})}{(1+e^{(-z^{(4)})})(1+e^{(z^{(4)})})} =(1+e(−z(4)))(1+e(z(4)))(1−y−ye−z(4))(1+e(z(4)))
= 1 − y ( 1 − e ( − z ( 4 ) ) ) ( 1 + e ( − z ( 4 ) ) ) =\frac{1-y(1-e^{(-z^{(4)})})}{(1+e^{(-z^{(4)})})} =(1+e(−z(4)))1−y(1−e(−z(4)))
= 1 1 + e − z ( 4 ) − y =\frac{1}{1+e^{-z^{(4)}}}-y =1+e−z(4)1−y
= g ( z ( 4 ) ) − y =g(z^{(4)})-y =g(z(4))−y
= a ( 4 ) − y =a^{(4)}-y =a(4)−y
即证得 δ 4 = a ( 4 ) − y \delta^{4}=a^{(4)}-y δ4=a(4)−y
故对于输出层L
∂ ∂ θ ( L − 1 ) J ( θ ) = a ( L − 1 ) δ ( L ) \frac{\partial}{\partial \theta^{(L-1)}}J(\theta)=a^{(L-1)}\delta^{(L)} ∂θ(L−1)∂J(θ)=a(L−1)δ(L)
δ L = a ( L ) − y \delta^{L}=a^{(L)}-y δL=a(L)−y
∂ ∂ θ ( 2 ) J ( θ ) = ∂ J ( θ ) ∂ z ( 3 ) ∂ z ( 3 ) ∂ θ ( 2 ) = δ ( 3 ) ∂ z ( 3 ) ∂ θ ( 2 ) = a ( 2 ) δ ( 3 ) \frac{\partial}{\partial{\theta^{(2)}}}J(\theta)=\frac{\partial{J(\theta)}}{\partial{z^{(3)}}}\frac{\partial{z^{(3)}}}{\partial{\theta^{(2)}}}=\delta^{(3)}\frac{\partial{z^{(3)}}}{\partial{\theta^{(2)}}}=a^{(2)}\delta^{(3)} ∂θ(2)∂J(θ)=∂z(3)∂J(θ)∂θ(2)∂z(3)=δ(3)∂θ(2)∂z(3)=a(2)δ(3)
δ ( 3 ) = ∂ J ( θ ) ∂ z ( 4 ) ∂ z ( 4 ) ∂ a ( 3 ) ∂ a ( 3 ) ∂ z ( 3 ) \delta^{(3)}=\frac{\partial{J(\theta)}}{\partial{z^{(4)}}}\frac{\partial{z^{(4)}}}{\partial{a^{(3)}}}\frac{\partial{a^{(3)}}}{\partial{z^{(3)}}} δ(3)=∂z(4)∂J(θ)∂a(3)∂z(4)∂z(3)∂a(3)
= δ ( 4 ) θ ( 3 ) ∂ a ( 3 ) ∂ z ( 3 ) =\delta^{(4)}\theta^{(3)}\frac{\partial{a^{(3)}}}{\partial{z^{(3)}}} =δ(4)θ(3)∂z(3)∂a(3)
sigmoid函数求导:
g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1
g ′ ( z ) = e − z ( 1 + e − z ) 2 g^{'}(z)=\frac{e^{-z}}{(1+e^{-z})^{2}} g′(z)=(1+e−z)2e−z
= 1 1 + e − z e − z 1 + e − z =\frac{1}{1+e^{-z}}\frac{e^{-z}}{1+e^{-z}} =1+e−z11+e−ze−z
= 1 1 + e − z ( 1 + e − z 1 + e − z − 1 1 + e − z ) =\frac{1}{1+e^{-z}}(\frac{1+e^{-z}}{1+e^{-z}}-\frac{1}{1+e^{-z}}) =1+e−z1(1+e−z1+e−z−1+e−z1)
= g ( z ) ( 1 − g ( z ) ) =g(z)(1-g(z)) =g(z)(1−g(z))
由于 a ( 3 ) = ( g ( z ( 3 ) ) 添 加 偏 置 项 a 0 = 1 a^{(3)}=(g(z^{(3)})添加偏置项a_{0}=1 a(3)=(g(z(3))添加偏置项a0=1,则
∂ a ( 3 ) ∂ z ( 3 ) = g ( z ( 3 ) ) ( 1 − g ( z ( 3 ) ) ) = a ( 3 ) . ∗ ( 1 − a ( 3 ) ) \frac{\partial{a^{(3)}}}{\partial{z^{(3)}}}=g(z^{(3)})(1-g(z^{(3)}))=a^{(3)}.*(1-a^{(3)}) ∂z(3)∂a(3)=g(z(3))(1−g(z(3)))=a(3).∗(1−a(3))
所以 δ 3 = ( θ ( 3 ) ) T δ 4 . ∗ a ( 3 ) . ∗ ( 1 − a ( 3 ) ) \delta^{3}=(\theta^{(3)})^{T}\delta^{4}.*a^{(3)}.*(1-a^{(3)}) δ3=(θ(3))Tδ4.∗a(3).∗(1−a(3))
故而对于隐藏层:
∂ ∂ θ ( l ) J ( θ ) = a ( l ) δ ( l + 1 ) \frac{\partial}{\partial{\theta^{(l)}}}J(\theta)=a^{(l)}\delta^{(l+1)} ∂θ(l)∂J(θ)=a(l)δ(l+1)
δ 3 = ( θ ( l ) ) T δ l + 1 . ∗ a ( l ) . ∗ ( 1 − a ( l ) ) \delta^{3}=(\theta^{(l)})^{T}\delta^{l+1}.*a^{(l)}.*(1-a^{(l)}) δ3=(θ(l))Tδl+1.∗a(l).∗(1−a(l))
3另一种证明方法
上面的推导过程是针对吴恩达机器学习视频的一个推导,下面介绍一种新的推导过程。
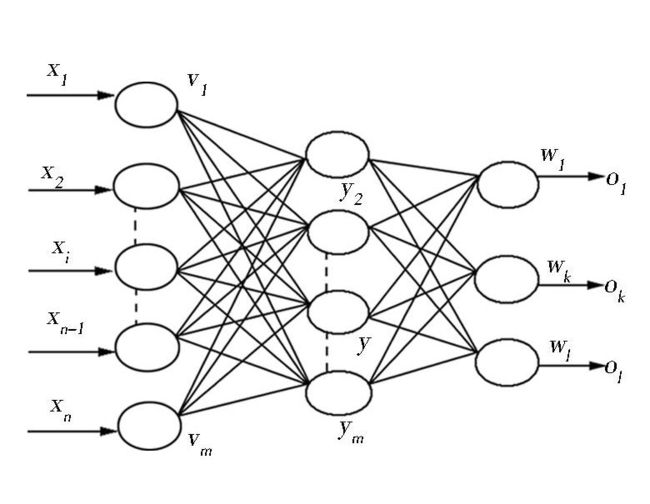
在如图所示神经网络中,输入向量为X
隐藏层输出向量为Y
输出层输出向量为O
输入层到隐藏层的权值矩阵为V
隐藏层到输出层的权值矩阵为W
对于输出层:
o k = f ( n e t k ) o_{k}=f(net_{k}) ok=f(netk)
n e t k = ∑ j = 0 l = w j , k y j net_{k}=\sum_{j=0}^{l}=w_{j,k}y_{j} netk=j=0∑l=wj,kyj
对于隐藏层:
y j = f ( n e t j ) y_{j}=f(net_{j}) yj=f(netj)
n e t j = ∑ i = 0 m = v i , j x i net_{j}=\sum_{i=0}^{m}=v_{i,j}x_{i} netj=i=0∑m=vi,jxi
f为sigmoid函数。
输出误差E(代价函数):
E = 1 2 ( d − o ) 2 = 1 2 ∑ k = 1 l ( d k − o k ) 2 … … … … ① E=\frac{1}{2}(d-o)^{2}=\frac{1}{2}\sum_{k=1}^{l}{(d_{k}-o_{k})^{2}}…………① E=21(d−o)2=21k=1∑l(dk−ok)2…………①
展开至隐藏层:
E = 1 2 ∑ k = 1 l ( d k − f ( ∑ j = 0 m w j k y j ) 2 … … … … ② E=\frac{1}{2}\sum_{k=1}^{l}{(d_{k}-f(\sum_{j=0}^{m}{w_{jk}y_{j}})^{2}}…………② E=21k=1∑l(dk−f(j=0∑mwjkyj)2…………②
展开到输入层:
E = 1 2 ∑ k = 1 l ( d k − f ( ∑ j = 0 m w j k ∑ i = 0 m v i j x i ) 2 E=\frac{1}{2}\sum_{k=1}^{l}{(d_{k}-f(\sum_{j=0}^{m}{w_{jk}\sum_{i=0}^{m}{v_{ij}x_{i}}})^{2}} E=21k=1∑l(dk−f(j=0∑mwjki=0∑mvijxi)2
由上面的公式可以得知E是关于w和v的函数,因此调整E的大小,就可以调整权重,因此将E作为代价函数。
仍然使用梯度下降法来使误差不断减小。
Δ w j k = − α ∂ E ∂ w j k = − α ∂ E ∂ n e t k ∂ n e t k ∂ w j k \Delta w_{jk}=-\alpha\frac{\partial E}{\partial w_{jk}}=-\alpha\frac{\partial E}{\partial net_{k}}\frac{\partial net_{k}}{\partial w_{jk}} Δwjk=−α∂wjk∂E=−α∂netk∂E∂wjk∂netk
Δ v i j = − α ∂ E ∂ v i j = − α ∂ E ∂ n e t j ∂ n e t j ∂ v i j \Delta v_{ij}=-\alpha\frac{\partial E}{\partial v_{ij}}=-\alpha\frac{\partial E}{\partial net_{j}}\frac{\partial net_{j}}{\partial v_{ij}} Δvij=−α∂vij∂E=−α∂netj∂E∂vij∂netj
令 δ k o = − ∂ E ∂ n e t k \delta^{o}_{k}=-\frac{\partial E}{\partial net_{k}} δko=−∂netk∂E
δ j y = − ∂ E ∂ n e t j \delta^{y}_{j}=- \frac{\partial E}{\partial net_{j}} δjy=−∂netj∂E
所以
由于 n e t k = ∑ j = 0 l = w j , k y j net_{k}=\sum_{j=0}^{l}=w_{j,k}y_{j} netk=∑j=0l=wj,kyj, n e t j = ∑ i = 0 m = v i , j x i net_{j}=\sum_{i=0}^{m}=v_{i,j}x_{i} netj=∑i=0m=vi,jxi,
所以 ∂ n e t k ∂ w j k = y j \frac{\partial net_{k}}{\partial w_{jk}}=y_{j} ∂wjk∂netk=yj, ∂ n e t j ∂ v i j = x i \frac{\partial net_{j}}{\partial v_{ij}}=x_{i} ∂vij∂netj=xi
Δ w j k = − α ∂ E ∂ n e t k ∂ n e t k ∂ w j k = α δ k o y j … … ③ \Delta w_{jk}=-\alpha\frac{\partial E}{\partial net_{k}}\frac{\partial net_{k}}{\partial w_{jk}}=\alpha\delta^{o}_{k}y_{j} ……③ Δwjk=−α∂netk∂E∂wjk∂netk=αδkoyj……③
Δ v i j = − α ∂ E ∂ n e t j ∂ n e t j ∂ v i j = α δ j y x i … … ④ \Delta v_{ij}=-\alpha\frac{\partial E}{\partial net_{j}}\frac{\partial net_{j}}{\partial v_{ij}}=\alpha\delta^{y}_{j}x_{i}……④ Δvij=−α∂netj∂E∂vij∂netj=αδjyxi……④
下面计算 δ k 0 \delta^{0}_{k} δk0, δ j y \delta^{y}_{j} δjy
δ k o = − ∂ E ∂ n e t k = − ∂ E ∂ o k ∂ o k ∂ n e t k \delta^{o}_{k}=-\frac{\partial E}{\partial net_{k}}=-\frac{\partial E}{\partial o_{k}}\frac{\partial o_{k}}{\partial net_{k}} δko=−∂netk∂E=−∂ok∂E∂netk∂ok
δ j y = − ∂ E ∂ n e t j = − ∂ E ∂ y j ∂ y j ∂ n e t j \delta^{y}_{j}=-\frac{\partial E}{\partial net_{j}}=-\frac{\partial E}{\partial y_{j}}\frac{\partial y_{j}}{\partial net_{j}} δjy=−∂netj∂E=−∂yj∂E∂netj∂yj
o k = f ( n e t k ) o_{k}=f(net_{k}) ok=f(netk),所以 ∂ o k ∂ n e t k = f ′ ( n e t k ) = o k ( 1 − o k ) \frac{\partial o_{k}}{\partial net_{k}}=f^{'}(net_{k})=o_{k}(1-o_k) ∂netk∂ok=f′(netk)=ok(1−ok)
y j = f ( n e t j ) y_{j}=f(net_{j}) yj=f(netj),所以 ∂ y j ∂ n e t j = f ′ ( n e t j ) = y j ( 1 − y j ) \frac{\partial y_{j}}{\partial net_{j}}=f^{'}(net_{j})=y_{j}(1-y_{j}) ∂netj∂yj=f′(netj)=yj(1−yj)
此处是有sigmoid函数求导的性质得来的,在上一部分已经证明过。
有式①得 ∂ E ∂ o k = − ( d k − o k ) \frac{\partial E}{\partial o_{k}}=-(d_{k}-o_{k}) ∂ok∂E=−(dk−ok)
由式②得 ∂ E ∂ y j = − ∑ k = 1 l ( d k − o k ) f ′ ( n e t k ) w j k \frac{\partial E}{\partial y_{j}}=-\sum_{k=1}^{l}(d_{k}-o_{k})f^{'}(net_{k})w_{jk} ∂yj∂E=−∑k=1l(dk−ok)f′(netk)wjk
δ k o = ∂ E ∂ o k ∂ o k ∂ n e t k \delta^{o}_{k}=\frac{\partial E}{\partial o_{k}}\frac{\partial o_{k}}{\partial net_{k}} δko=∂ok∂E∂netk∂ok
= ( d k − o k ) o k ( 1 − o k ) =(d_{k}-o_{k})o_{k}(1-o_{k}) =(dk−ok)ok(1−ok)
δ j y = ∂ E ∂ y j ∂ y j ∂ n e t j \delta^{y}_{j}=\frac{\partial E}{\partial y_{j}}\frac{\partial y_{j}}{\partial net_{j}} δjy=∂yj∂E∂netj∂yj
= ∑ k = 1 l ( d k − o k ) f ′ ( n e t k ) w j k y j ( 1 − y j ) =\sum_{k=1}^{l}(d_{k}-o_{k})f^{'}(net_{k})w_{jk}y_{j}(1-y_{j}) =∑k=1l(dk−ok)f′(netk)wjkyj(1−yj)
= ∑ k = 1 l ( d k − o k ) o k ( 1 − o k ) w j k y i ( 1 − y i ) =\sum_{k=1}^{l}(d_{k}-o_{k})o_{k}(1-o_{k})w_{jk}y_{i}(1-y_{i}) =∑k=1l(dk−ok)ok(1−ok)wjkyi(1−yi)
= ( ∑ k = 1 l δ k o w j k ) y i ( 1 − y i ) =(\sum_{k=1}^{l}\delta^{o}_{k}w_{jk})y_{i}(1-y_{i}) =(∑k=1lδkowjk)yi(1−yi)
由式③和④得:
Δ w j k = α ( d k − o k ) o k ( 1 − o k ) y j \Delta w_{jk}=\alpha(d_{k}-o_{k})o_{k}(1-o_{k})y_{j} Δwjk=α(dk−ok)ok(1−ok)yj
Δ = α ( ∑ k = 1 l δ k o w j k ) y i ( 1 − y i ) x i \Delta=\alpha(\sum_{k=1}^{l}\delta^{o}_{k}w_{jk})y_{i}(1-y_{i})x_{i} Δ=α(k=1∑lδkowjk)yi(1−yi)xi
该种方法构造出得代价函数虽然与上边的代价函数不一样,但是其思想都是一样的,就是通过梯度下降法来不断使代价函数的值减小,从而使模型参数发生了改变,知道寻找到合适的模型参数为止。两种方法的推导过程也是要用到链式法则,层层来求导。