利用Python计算离散点构成曲线的曲率
目录
- 一、实现原理
-
- 1.1、计算点到直线的距离——海伦公式
- 参考链接
计算曲率就是为了求这段弧长对应的半径,也就是说,我们把曲线看成圆的弧长就行,那么问题就简单了。
一、实现原理
1.1、计算点到直线的距离——海伦公式
如下图所示,要计算 A 到 CB 的长度 d \pmb{d} d, d \pmb{d} d 越大曲率越大。
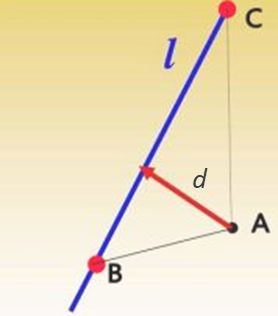
设 Δ \Delta ΔABC 的三条边分别为 a,b,c, 那么海伦公式计算面积 S 如下:
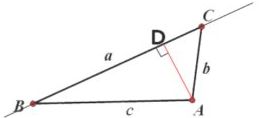
S = p ( p − a ) ( p − b ) ( p − c ) 其中: p = 1 2 ( a + b + c ) \begin{aligned} S=\sqrt{p(p-a)(p-b)(p-c)}& \\ 其中:p=\frac{1}{2}(a+b+c)& \end{aligned} S=p(p−a)(p−b)(p−c)其中:p=21(a+b+c)
如下图所示,AD 是 A 到直线 BC 的距离,即 AD 是 ΔABC 边 BC 上的高,
from scipy.spatial.distance import pdist
for i in range(len(x2 - 2)):
x = (x2[i] - x2[i - 1], y2[i] - y2[i - 1])
y = (x2[i + 1] - x2[i], y2[i + 1] - y2[i])
d = 1 - pdist([x, y], 'cosine')
sin = np.sqrt(1 - d ** 2)
dis = np.sqrt((x2[i - 1] - x2[i + 1]) ** 2 + (y2[i - 1] - y2[i + 1]) ** 2)
k = 2 * sin / dis
print(k)
参考链接
[1] https://blog.csdn.net/wxplol/article/details/122360840;
[2] Python中离散点如何求曲率?;