AdaQuant:改进训练后神经网络量化:分层校准和整数编程
AdaQuant:改进训练后神经网络量化:分层校准和整数编程
-
-
- 摘要
- 方法
-
- AdaQuant:在校准数据集上的逐层量化
-
- 校验集的大小
- Integer Programming:实现每层的比特分配
-
- 基本公式
- Batch-Norm Tuning
-
- 重构BN层
- 重新融合BN层
- 偏置调整
- Quantization Flow
- 实验结果
-
- AdaQuant
- Integer Programming
- Batch-Norm Tuning
- Full pipeline and ablation study
-
本文是以色列理工学院与英特尔联合提出的基于PTQ的神经网络量化技术,并且提出了不同复杂度下的量化策略方案与基于整数编程的混合精度搜索。实现了ResNet50 MergeBN下模型权重与激活的4bit量化,且精度损失不到1%。
- 论文题目:Improving Post Training Neural Quantization: Layer-wise Calibration and Integer Programming
- 论文链接:https://arxiv.org/abs/2006.10518
- 代码链接:https://github.com/itayhubara/CalibTIP
摘要
训练后量化方法使用简单,并且只需要少量未标记的校准集,因此引起了相当大的关注。在没有明显过拟合的情况下,这个小的数据集不能用于微调模型。相反,这些方法仅使用校准集来设置激活的动态范围。但是,当使用低于8位的格式时(除非在小型数据集上使用),此类方法始终会导致精度显着下降。本文旨在突破8位的障碍。为此,通过在校准集上优化每一层的参数,分别最小化每一层的量化误差。本文从实验角度证明这种方法:(1)与标准的微调方法相比,对过拟合的敏感度要低得多,并且即使在非常小的校准集上也可以使用; (2)比以前的方法(仅能设置激活的动态范围)更强大。此外,本文提出一种新颖的整数编程公式,在为每层精确分配位宽的同时,限制了精度的降低。最后,本文建议对全局统计信息进行模型调整,以纠正量化期间引入的偏差。这些方法结合在视觉和文本任务上取得了SOTA的结果。例如,在ResNet50上,实现了所有层权重和激活4-bit量化,且精度下降不到1%。
方法
在大多数训练后量化设置中,会提供一个模型和一个小的未标记校准集。 为了避免过度拟合校准集,大多数研究仅将其用于提取网络的内部统计信息,然后将其用于设置量化参数。
在这里,本文建议更广泛地使用校准集来调整模型,同时避免过度拟合数据。 在以下小节中,将详细介绍校准集上的三种不同的优化方法:(1)AdaQuant,权重和量化参数的分层优化; (2)用于混合精度设置的整数编程公式;(3)批量归一化调整(BNT),用于调整模型的内部统计信息以匹配数字精度设置。 本文讨论了每种方法的优点和缺点,并提出了一种优化流程,该流程可以利用所有附加优点,并得出SOTA的结果。
AdaQuant:在校准数据集上的逐层量化
一些研究人员建议按 per-tensor 优化,以通过最小化量化张量和全精度张量 X 之间的某种形式的MSE目标(权重或激活)来减少量化误差。 他们通过以下公式,寻找最优的量化步长 Δ ^ \hat{\Delta} Δ^。
Δ ^ = arg min Δ ∥ X − Q Δ ( X ) ∥ 2 ; Q Δ ( X ) = Δ ⋅ ⌊ X Δ ⌉ ( 1 ) \hat{\Delta}=\underset{\Delta}{\arg \min }\left\|X-Q_{\Delta}(X)\right\|^{2} ; \quad Q_{\Delta}(X)=\Delta \cdot\left\lfloor\frac{X}{\Delta}\right\rceil \quad (1) Δ^=Δargmin∥X−QΔ(X)∥2;QΔ(X)=Δ⋅⌊ΔX⌉(1)
其中 Q(·) 是量化函数。 尽管这些方法快速且易于使用,但它们通常会导致解决方案的变差,由于公式(1)的损失是次优的,所以它会同等地惩罚所有量化误差。 但是,这种损失应该对更多影响分类的量化误差进行惩罚。 因此,研究人员建议采用量化意识训练(QAT)方法,通过立即训练整个模型来解决此错误。 但是,这些方法具有三个局限性:(a)他们需要庞大的训练集来避免过度拟合;(b)它们通过离散函数(量化器)来近似反向传播梯度;(c)它们需要高计算量和存储能力。 本文建议修改目标为对权重和量化参数进行逐层联合的优化。
( Δ ^ w , Δ ^ x , V ^ ) = arg min Δ w , Δ x , V ∥ W X − Q Δ w ( W + V ) ⋅ Q Δ x ( X ) ∥ 2 ( 2 ) \left(\hat{\Delta}_{w}, \hat{\Delta}_{x}, \hat{V}\right)=\underset{\Delta_{w}, \Delta_{x}, V}{\arg \min }\left\|W X-Q_{\Delta_{w}}(W+V) \cdot Q_{\Delta_{x}}(X)\right\|^{2} \quad (2) (Δ^w,Δ^x,V^)=Δw,Δx,Vargmin∥WX−QΔw(W+V)⋅QΔx(X)∥2(2)
其中 V 是加到 W 的连续变量,量化的网络权重定义为 W q = Q Δ ˙ w ( W + V ^ ) W_{q}=Q_{\dot{\Delta}_{w}}(W+\hat{V}) Wq=QΔ˙w(W+V^)。在这个新的目标中,不需要量化张量“接近”原始张量,如公式(1),受益于量化意识训练方法的灵活性。 但是,它可以在所有层上并行执行,并且不太容易出现过拟合的情况。此外,在固定配置下,本文可以全局优化模型并推断层之间的误差。 因此,可以顺序运行它,而不是在所有层上并行运行 AdaQuant 并修正由于量化前几层而引起的误差。 因此,公式(2)更改为以下公式,其中 σ(·) 表示激活函数:
( Δ ^ w l , Δ ^ x l , V ^ l ) = arg min Δ w l , Δ x l , V l ∥ W l X l − Q Δ w l ( W l + V l ) ⋅ Q Δ x l ( X l q ) ∥ 2 ( 3 ) \left(\hat{\Delta}_{w_{l}}, \hat{\Delta}_{x_{l}}, \hat{V}_{l}\right) =\underset{\Delta_{w_{l}}, \Delta_{x_{l}}, V_{l}}{\arg \min }\left\|W_{l} X_{l}-Q_{\Delta_{w_{l}}}\left(W_{l}+V_{l}\right) \cdot Q_{\Delta_{x_{l}}}\left(X_{l}^{q}\right)\right\|^{2} \quad (3) (Δ^wl,Δ^xl,V^l)=Δwl,Δxl,Vlargmin∥∥∥WlXl−QΔwl(Wl+Vl)⋅QΔxl(Xlq)∥∥∥2(3)
X q = σ ( Q Δ w l − 1 ( W l − 1 + V l − 1 ) ⋅ Q Δ x l ( X l − 1 q ) ) ( 4 ) X_{q} =\sigma\left(Q_{\Delta_{w_{l-1}}}\left(W_{l-1}+V_{l-1}\right) \cdot Q_{\Delta_{x_{l}}}\left(X_{l-1}^{q}\right)\right) \quad (4) Xq=σ(QΔwl−1(Wl−1+Vl−1)⋅QΔxl(Xl−1q))(4)
请注意,在设置位分配之前,不能应用 sequential-AdaQuant ,因为它可以优化从先前量化层获得的有噪声输入。 本文评估了 AdaQuant 的两个变量(分别命名为 AdQuant 和 sequential-AdaQuant,并在后面中详细介绍了本文的发现。注意,AdaQuant 还优化了偏差和偏移,并优化了存在的 conv-bn-relu 融合层; 为了简单起见,这些已从等式2中删除。
校验集的大小
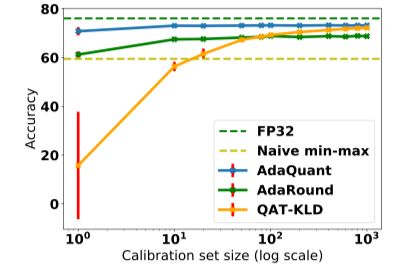
令人惊讶的是,尽管使用很小的校准集进行实验,但未观察到过度拟合。以一个简单的全连接层 W ∈ R M × N W \in R^{M×N} W∈RM×N。输入和输出的大小分别为 N 和 M。对于每个输出,有 B 个方程式和 N 个单独的参数(即,不同输出之间的参数没有重叠)。因此,如果B = N,一般会有无限数量的解,可以覆盖数据。如果B ≫ N,那么我们可能会欠缺数据。因此,AdaQuant 所需的校准集的大小应大致为O(N)。卷积层的类似推导表明,校准大小应具有 B ≥ C i ⋅ k 2 H W B \geq \frac{C_{i} \cdot k^{2}}{H W} B≥HWCi⋅k2 个样本,以避免过度拟合,其中 B 是唯一样本的数量,k 是卷积的内核大小, C i C^i Ci 和 C o C^o Co 是输入和输出通道的数量,H,W分别代表高度和宽度。在下图中,将 AdaQuant 与当前最先进的方法进行了比较,包括 QAT 与知识蒸馏(QAT-KLD)和AdaRound。对于每种方法,在五次运行中相对于校准集中的样品数量测量了 Top-1 准确性,并给出了平均值和标准偏差。可以看出,AdaQuant 优于以前的方法,并且在小型校准集上尤为出色。值得注意的是,即使在单个图像上进行优化,AdaQuant 也不会过度拟合。
Integer Programming:实现每层的比特分配
AdaQuant 显着提高了较低位宽时的网络精度。但是,它本身往往不足以达到可接受的精度。因此,在实际使用情况下,用户希望通过将多个层设置为更高的精度来在精度和性能(例如,功率和速度)之间取得平衡。在本节中,本文的高层目标是优化总体网络性能,同时保持预定的精度下降或模型压缩约束。
本文提供了一种整数编程(IP)公式,用于优化每层比特分配。根据需要,我们的性能指标 P 可以是网络的执行时间或其功耗。同样,对于每一层量化,都有一个相关的量化误差会影响训练损失 L。我们选择后者作为惩罚度量。整数编程适用于可以明确地以不同决策变量之间的线性关系形式表示给定问题的情况。与以前的其他压缩工作不同,它可以达到全局最优。例如,文章 “ Fixed point quantization of deep convolutional networks ” 提出了凸优化问题,但约束和目标不是线性的。这通常会对收敛时间产生极大的影响,并且由于不再可以使用单纯形法,因此结果的质量也会受到影响。
基本公式
我们得到了具有 L 层的神经网络。对于每个层 l l l,我们都需要将权重 W l W_l Wl与上一层 X l − 1 X_{l-1} Xl−1 的激活相乘。可以通过量化权重和激活来执行这种较低的位宽乘法,以实现更高的吞吐量和高能效的解决方案。令 W l k W^k_l Wlk和 X l − 1 n X^n_{l-1} Xl−1n分别表示 W l W_l Wl和 X l − 1 X_{l-1} Xl−1到 k 和 n 位的量化版本。对于每一层i,相对于原始乘积 W l ⋅ X l − 1 W_l \cdot X_{l-1} Wl⋅Xl−1,低比特宽度的乘积 W l k ⋅ X l − 1 n W^k_l \cdot X^n_{l-1} Wlk⋅Xl−1n 可以实现 Δ L l k , n \Delta \mathcal{L}_{l}^{k, n} ΔLlk,n的损耗降低和 Δ P l k , n \Delta \mathbb{P}_{l}^{k, n} ΔPlk,n 的性能改善。这种性能改进措施需要加和,并总结出端到端网络性能(例如,功率,模型大小等)的总收益。我们的目标是在不超过总网络降级L的情况下最大程度地提高总体性能。本文使用整数程序来解决上述问题。定义一个二进制变量 $I_{l}^{k, n} $,当且仅当权重 W l k W^k_l Wlk 与层 l l l 的激活 X l − 1 n X^n_{l-1} Xl−1n 相乘时,才将其设置为1。否则,将指标设置为零,即 I l k , n = 0 I_{l}^{k, n}=0 Ilk,n=0。然后,基本比特分配问题可以表述为:
Maximize ∑ l = 0 L − 1 Δ P l ( 1 a ) Subject to ∑ l Δ L l ≤ Δ L , ( 1 b ) ∀ l ∈ { 1 , … , L } : Δ P l = ∑ k , n I l k , n ⋅ Δ P l k , n , Δ L l = ∑ k , n I l k , n ⋅ Δ L l k , n ( 1 c ) ∀ l ∈ { 1 , … , L } : ∑ k , n I l k , n = 1 , I l k , n ∈ { 0 , 1 } ( 1 d ) \begin{array}{c} \text { Maximize } \sum_{l=0}^{L-1} \Delta \mathbb{P}_{l} \quad (1a) \\ \text { Subject to } \sum_{l} \Delta \mathcal{L}_{l} \leq \Delta \mathcal{L}, \quad (1b)\\ \forall l \in\{1, \ldots, L\}: \Delta \mathbb{P}_{l}=\sum_{k, n} I_{l}^{k, n} \cdot \Delta \mathbb{P}_{l}^{k, n}, \Delta \mathcal{L}_{l}=\sum_{k, n} I_{l}^{k, n} \cdot \Delta \mathcal{L}_{l}^{k, n} \quad (1c)\\ \forall l \in\{1, \ldots, L\}: \sum_{k, n} I_{l}^{k, n}=1, I_{l}^{k, n} \in\{0,1\} \quad (1d) \end{array} Maximize ∑l=0L−1ΔPl(1a) Subject to ∑lΔLl≤ΔL,(1b)∀l∈{1,…,L}:ΔPl=∑k,nIlk,n⋅ΔPlk,n,ΔLl=∑k,nIlk,n⋅ΔLlk,n(1c)∀l∈{1,…,L}:∑k,nIlk,n=1,Ilk,n∈{0,1}(1d)
目标函数(1a)使总体性能提高最大化。 约束(1b)和(1c)确保由于层 l l l 被量化为 k 比特权重和 n 比特激活而导致的损失的总体降低和性能的总体改善将分别为 Δ L l \Delta \mathcal{L}_{l} ΔLl 和 Δ P l \Delta \mathbb{P}_{l} ΔPl。 公式(1d)指出,要遵守对 L 的总降解的限制,并确保每层仅选择一种配置(具有量化的权重和激活)。
Batch-Norm Tuning
一种常见的做法是在应用后训练量化以减少乘法累加(MAC)操作量之前,将BN层融合到其先前的权重层中。 但是,量化后比特宽度的减少会导致模型的内部统计数据与全精度模型的统计数据进一步偏离。 为了补偿这种偏差,应该更新 BN 统计信息。 首先,需要重建BN层,然后重新调整BN层的统计信息(通过运行均值的几次迭代来重新收集统计信息)。 最后,将BN层重新融合到权重层中(这仅在当前标准的per-channel权重量化设置中才有可能)。 接下来,将提供有关每个阶段的更多详细信息。
重构BN层
假定原始的(预融合)BN参数 γ o , β o \gamma_{o},\beta_{o} γo,βo 是已知的。 我们首先初始化 μ , σ 2 \mu,\sigma^{2} μ,σ2以及BN参数 σ r \sigma_{r} σr和 β r \beta_{r} βr(r表示“重构”)
B N r ( x ) = γ r x − μ σ 2 + ϵ + β r ≈ x B N_{r}(x)=\gamma_{r} \frac{x-\mu}{\sqrt{\sigma^{2}+\epsilon}}+\beta_{r} \approx x BNr(x)=γrσ2+ϵx−μ+βr≈x
为此,首先通过设置以下参数(用r表示)来初始化重构的BN层:使 B N r ( x ) = x B N_{r}(x)=x BNr(x)=x
μ = β r = β o ; σ 2 = γ o 2 ; γ r = γ o 2 + ϵ \mu=\beta_{r}=\beta_{o} ; \quad \sigma^{2}=\gamma_{o}^{2} \quad ; \gamma_{r}=\sqrt{\gamma_{o}^{2}+\epsilon} μ=βr=βo;σ2=γo2;γr=γo2+ϵ
然后,通过收集校准数据上的滑动均值和滑动方差来更新 μ , σ 2 \mu,\sigma^{2} μ,σ2。在应用BN调整时,BN参数 γ r , β r \gamma_{r},\beta_{r} γr,βr 不会改变,因为仅需调用前向传播。
重新融合BN层
由于使用的 per-channel 量化设置,可以将收集到的统计信息重新融合到当前的量化比例中,如下所示:
W i ′ = W i γ r σ ; b i ′ = γ r σ ( b i − μ ) + β r ; Δ w i ′ = γ r σ Δ w i W_{i}^{\prime}=W_{i} \frac{\gamma_{r}}{\sigma} ; \quad b_{i}^{\prime}=\frac{\gamma_{r}}{\sigma}\left(b_{i}-\mu\right)+\beta_{r} ; \quad \Delta_{w_{i}}^{\prime}=\frac{\gamma_{r}}{\sigma} \Delta_{w_{i}} Wi′=Wiσγr;bi′=σγr(bi−μ)+βr;Δwi′=σγrΔwi
因此,除了常规的 BN 融合之外,量化步长还通过 γ r σ − 1 \gamma_{r}\sigma^{-1} γrσ−1 进行调整。
偏置调整
对最终的混合精度模型应用全局偏差调整,方法是应用量化感知训练以最大程度地减少知识蒸馏(KD)损失(不需要标签)。 由于将可训练变量限制为仅偏差,因此即使在校准集上进行训练而不会出现过度拟合。
Quantization Flow
过去几年中,高效部署技术迅速发展。部署流程可能会因用户设置而异,例如硬件限制,部署时间和任务/数据集可用性。尽管有些用户愿意在初始化时付出时间和精力来获得另一部分精度,但其他用户则需要一种简单而快速的解决方案。为了解决这个问题,本文提出了两个新颖的 Pipeline,即 Light-Pipeline 和 Heavy-Pipeline。流水线是针对当前最常见的设置而设计的:per-channel 量化以及少量校准集。
Light-Pipeline 需要三个步骤:
- (1)融合层和定义量化参数;
- (2)使用IP找到最佳的混合精度配置;
- (3)使用BN调整来校正内部统计数据。
注意,所有步骤都不需要反向传播,因此非常轻便,快速。
在 Heavy-Pipeline 中,应用 AdaQuant 来降低各层在调用IP算法之前的全精度对应输出失真。表1中给出了两个管道之间的详细比较。可以无缝拼接使用AdaQuant优化为不同位宽的模型,从而能够在混合精度设置中创建优化模型。随后,可以应用诸如调整BN统计信息和各层偏差之类的全局方法来减少知识提取的损失。尽管还有其他训练后量化技术可以与我们的方法潜在地结合起来,例如偏差校正,均衡和离群的信道拆分,但是,并没有必要。本文的结果表明,即使不结合使用此类方法,采用相对简单的 Pipeline 也可以在视觉模型和文本模型上产生 SOTA 的准确性。
实验结果
AdaQuant
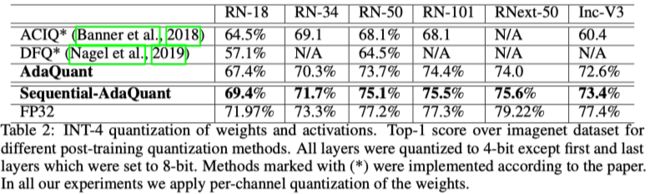
最近,一些研究人员提出了不同类型的MSE优化。在大多数情况下,优化是按per-tensor完成的(即分别针对权重和激活量)。在这里,本文认为,通过同时优化量化参数和权重,可以进一步降低MSE,从而提高精度,如图2b所示。与AdaRound相反,该方法将权重的变化限制在±1以内,本文允许根据需要改变权重。在图2a中,权重确实将其量化值改变了不止一个。由于本文专注于混合精度设置,因此在拼接优化模型时,将分别优化每一层,以实现最大的灵活性。在此设置下,可以在所有层上并行执行AdaQuant。但是,由于最近的论文并没有显示完整的压缩精度曲线,只有少数尝试进行4位压缩,因此本文也使用顺序AdaQuant校正器将结果与常见的固定配置进行了比较。虽然 sequential-AdaQuant 无法并行化或用于混合精度设置,但它可以为所有测试的模型提供最佳的结果,如表2和表3所示。例如,在广泛研究的8位MobileNet-V2(MobileNet -V2)拓扑,top-1精度达到了71.6%,与全精度(71.9%)相比,降级幅度不到0.5%。
Integer Programming
整数编程公式要求每层具有两个要求:(1)损失降低;2)性能提高。要获得这些量化指标,需要在一个小的校准集L次(每层一次)上调用模型,并测量损失降低和性能增益。在实验中,将性能值设置为参数数量,但是此度量可以更改为任何加法度量。在所有实验中,本文使用了训练集中的1000个样本作为校准集。本文的设置仅考虑8位层和4位层的混合。为了进一步测试IP功能,还研究了2-4-8位的混合。不幸的是,由于训练后设置中的2位量化会导致较高的降级,因此IP算法仅选择4-8位的混合来实现高于12.5%的压缩率。然而,对于12.5%的压缩率,IP方法发现,通过将一层设置为2位,而将8个较小的层设置为8位,相对于统一的4位量化,其准确度提高了5.5%以上。另外,通过允许不太友好的硬件设置(数值精度可以是2-8之间的任何整数形式),可以产生最高的压缩精度比。
Batch-Norm Tuning
批归一化调整(BNT)具有显着优势,因为它不需要权重优化。 由于BNT是通过调用整个模型来应用的,因此,只有在设置混合精度位宽配置后,才必须应用BNT。 所有全局优化方法(包括偏差调整)都是这种情况。 值得注意的是,BNT只需在校准集中进行几次(最多10次)正向通过,即可获得显着的增益。 在这项研究中,仅在使用BN层训练的模型上应用了BNT。 但是,通过从统计数据中重建该方法,有可能将该方法扩展到没有BN层的模型。
Full pipeline and ablation study
尽管一些研究人员提出了用于训练后的混合精度量化的不同方法,但没有一个提供其代码。 每篇论文都侧重于不同的量化设置(例如,仅量化权重,按张量量化等)。 因此,为了展示Pipeline 实力,本文根据常见做法创建了两个不同的基准:
- 贪婪精度:最近的研究建议测量每个层的灵敏度,并根据压缩目标降低最坚固层的精度。
- 贪婪压缩:互补贪婪方法,根据参数数量对层进行排序,并从最小层到最大层增加层的精度,直到达到压缩预算为止。
出人意料的是,尽管层的大小应与其对量化的敏感性相关,但这两种贪婪方法却产生了完全不同的配置。研究配置贪婪压缩发现,按压缩排序与模型中各层的位置相关。在大多数视觉模型中,靠近输入的层具有较少的参数。这与当前的惯例一致。值得注意的是,即使不与任何其他技术结合使用,IP方法也能获得最佳的位宽配置,从而强调其重要性。
接下来,转向考虑 light and advanced pipelines。在具有挑战性的压缩率下,Light-Pipeline 测试结果凸显了BN调谐的重要性。从下图可以看出。只需在推理模式下调用模型几次迭代并修正中间统计信息,就可以恢复超过1.5%的准确度(73.7%vs.75.37%)。不出所料,通过应用 Heavy-Pipeline,可以获得最先进的精度。在0.13%的压缩率下,在将96%的模型转换为4位的同时,本文设法将精度保持在全精度的1%以内。对于具有挑战性的MobileNet-V2,本文设法将25%的层切换到4bit(权重和激活),同时保持不到2%的下降;此外,当几乎整个模型为4位时,第一次实现了合理的top-1精度,达到65%。
![]()