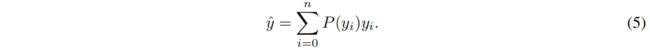Generalized Focal Loss 原理与代码解析

Paper：Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes for Dense Object Detection

背景

One-stage detector通常包含三个分支：分类、定位（边框回归）、定位质量估计。分类通常用Focal Loss进行优化，边框位置通常是在狄拉克分布下学习的，定位质量估计分支比如FCOS中的centerness通常与分类的置信度进行结合，以提升检测精度。

存在的问题

1、在训练和推理阶段定位质量估计与分类得分使用方法的不一致

这两个分支通常是独立训练的，但在推理阶段通过相乘结合起来使用。

定位质量估计只对正样本进行监督，这是不可靠的因为负样本有可能定位质量估计的得分非常高，在推理时分类得分与质量估计得分相乘后作为NMS的score进行排序时，有可能一个质量估计得分非常高的负样本排在了一个分类得分和质量估计得分都不那么高的正样本前面。

2、边界框回归的表示不够灵活

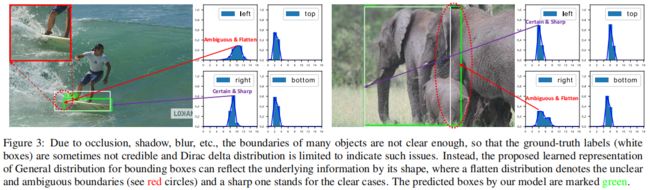
通常边界框回归表示是建模在迪拉克分布下的，这种表示没有考虑到实际数据集中模糊和不确定的边界情况。比如下图中的滑板和大象的gt边界因为遮挡不够准确。尽管有些方法将边框建模为高斯分布，但过于简单了，实际的分布可能更抽象和灵活而不像高斯函数那样具有对称性。

本文的创新点

为了解决上述问题，本文对边界框及其定位质量设计了新的表示方法。

定位质量表示。提出将其与分类得分合并为一个单一的统一表示，即一个分类向量中gt类别索引处的值是其对应的定位质量（通常是预测框和gt框的IoU），它既可以端到端的训练，也可以在推理时直接使用。

边界框表示。提出通过直接学习边界框位置在其连续空间上的离散分布，不引入任何其它更强的先验（比如高斯），来表示bounding box位置的任意分布。

通常分类分支采用Focal Loss进行优化，但FL只支持离散的标签比如0,1，但改进后的标签IoU是[0, 1]之间的连续值，因此本文提出了Generalized Focal Loss（GFL），它可以处理任意连续的标签。GFL具体又包括Quality Focal Loss（QFL）和Distribution Focal Loss（DFL），其中QFL用于优化分类和质量估计联合分支，DFL用于优化边框分支。

具体方法

原始的Focal Loss如下所示

其中 \(y\in \left \{ 1,0 \right \} \) 表示ground truth类别，\(p\in \left [ 0,1 \right ] \)表示 \(y=1\) 的估计概率，\(\gamma \) 是可调参数，FL由一个标准的交叉熵 \(-log(p_{t})\) 和一个动态缩放因子 \((1-p_{t})^{\gamma}\) 两部分组成，其中动态缩放因子在训练过程中自动降低易分样本的贡献，并让模型专注于难分样本。 

Quality Focal Loss（QFL）

为了解决之前提到的训练推理不一致的问题，本文提出了定位质量（IoU-score）和分类得分的联合表示，即将原本one-hot对应gt索引处的标签1换成[0, 1]区间的一个float值，即IoU。其中 \(y=0\) 表示负样本，\(y<0\le 1\) 表示正样本和其目标的IoU。和FL原论文一样，对于多类别，采用多个二分类sigmoid的 \(\sigma \left ( \cdot  \right ) \) 实现。为了简便，sigmoid的输出用 \(\sigma\) 表示。

由于样本不平衡的问题仍然存在，本文依然采用FL的思想，但原始的FL只支持离散的标签，本文对其形式进行了修改使其能够支持连续的label。具体包括交叉熵部分 \(-log(p_{t})\) 展开成其完整形式 \(-((1-y)log(1-\sigma)+ylog(\sigma))\)，缩放因子部分 \((1-p_{t})^{\gamma}\) 推广为估计 \(\sigma\) 和其连续标签 \(y\) 之间的绝对距离即 \(\left | y-\sigma \right | ^{\beta }(\beta\ge 0)\)，其中 \(\left | \cdot  \right | \) 保证了值非负，然后将两部分合并就得到了完整的Quality Focal Loss

Distribution Focal Loss（DFL）

和FCOS一样，本文采用点到bounding box四条边的距离作为回归的target，之前都是通过狄拉克分布对回归目标 \(y\) 进行建模 \(\delta (x-y)\)，它满足 \(\int_{-\infty }^{+\infty} \delta (x-y)dx=1\)，一般是通过全连接层实现的。还原 \(y\) 的积分形式如下 

和之前的狄拉克或高斯分布不同，本文提出不引入其它先验，直接学习其一般分布 \(P(x)\)，给定标签 \(y\) 的的取值范围最小值 \(y_{0}\) 和最大值 \(y_{n}(y_{0}\le y\le y_{n},n\in \mathbb N^{+})\)，从下式可得估计值 \(\hat{y} \)

为了方便网络优化，作者将连续区间上的积分转换成了离散的形式，通过将区间 \(\left [ y_{0},y_{n} \right ] \) 转换成一组等间隔 \(\triangle\)（为了方便取\(\triangle=1\)）的离散区间 \(\left \{ y_{0},y_{1},...,y_{i},y_{i+1},...,y_{n-1},y_{n} \right \} \)，根据离散分布的性质 \(\sum_{i=0}^{n} P(y_{i})=1\)，回归估计值可由下式得到

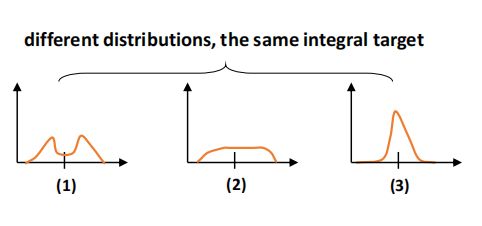
因此可通过一个包含 \(n+1\) 个单元的softmax层 \(S(\cdot)\) 得到 \(P(x)\)，为了方便 \(P(y_{i})\) 用 \(S_{i}\) 表示。\(\hat{y}\) 可用传统的loss函数如Smooth L1、IoU Loss、GIoU Loss进行端到端的训练，但是 \(P(x)\) 有无限种组合可以使最终的积分结果为 \(y\)，如下图所示，这会降低学习效率。

凭直觉(3)比(1)和(2)更紧凑，对边界框的估计更准确，这促使作者通过使越靠近目标 \(y\) 的值置信度更高来优化 \(P(x)\) 的形状。并且通常真实的分布不会离标注位置太远，因此作者提出了Distribution Focal Loss通过显式的增大最靠近标签 \(y\) 的两个整数 \(y_{i}\) 和 \(y_{i+1}\)(\(y_{i}\le y\le y_{i+1}\))的概率让网络快速定位到标签 \(y\) 附近的值，因此回归只针对正样本，不存在样本不平衡的问题，因此直接用交叉熵的形式定义DFL

完整的训练损失如下所示

其中 \(\mathcal{L}_{Q}\) 是QFL，\(\mathcal{L}_{D}\) 是DFL，\(\mathcal{L}_{B}\)是GIoU Loss，\(N_{pos}\) 表示正样本数量，\(\lambda_{0}\)（默认为2）和 \(\lambda_{1}\)（默认为\({ \frac{1}{4} } \)，4个方向的均值）是平衡权重。\(\mathbf{1} _{\left \{ c_{z}^{*}>0 \right \} }\) 是指示函数，若 \(c_{z}^{*}>0\) 值为1否则值为0。 

代码解析

以mmdetection中的实现为例，采用anchor-free的架构，正负样本分配采用ATSS。

下面是DFL的实现，其中输入pred.shape=(108, 17)，注意这里实际正样本个数是108/4=27，每个predicted box有四条边要回归。另外输入label是feature map上的点映射回原图后对应的点到gt box四边的实际距离除以对应步长得到的，因为设置离散区间长度为16，除以步长应该是为了让目标值落入[0, 16]这个区间。

def distribution_focal_loss(pred, label):
    r"""Distribution Focal Loss (DFL) is from `Generalized Focal Loss: Learning
    Qualified and Distributed Bounding Boxes for Dense Object Detection
    `_.

    Args:
        pred (torch.Tensor): Predicted general distribution of bounding boxes
            (before softmax) with shape (N, n+1), n is the max value of the
            integral set `{0, ..., n}` in paper.
        label (torch.Tensor): Target distance label for bounding boxes with
            shape (N,).

    Returns:
        torch.Tensor: Loss tensor with shape (N,).
    """
    dis_left = label.long()
    dis_right = dis_left + 1
    weight_left = dis_right.float() - label
    weight_right = label - dis_left.float()
    loss = F.cross_entropy(pred, dis_left, reduction='none') * weight_left \
        + F.cross_entropy(pred, dis_right, reduction='none') * weight_right
    return loss

下面是QFL的实现，其中对于多分类问题是将每一类单独看作二分类实现的，这和原始的Focal Loss中是一样的。另外下面的实现中是将正负样本项分开实现的。QFL将one-hot向量中目标类别索引位置的值由1换成了预测框和目标框的IoU，而预测框又是由对应的anchor point和学习到的到四条边的距离得到的，由上面的介绍可知到每个边的距离并不是向之前一样建模狄拉克分布直接学习距离值，而是学习某个区间上的一般离散分布，区间的长度包含实际的距离target，文中区间长度reg_max=16，间隔为1，因此到每个边的距离回归学习的是17个概率，一个点到四边的距离共学习4x(16+1)=68个概率值。根据学习到的概率值通过离散积分还原成学习到的距离，具体实现见下面的Integral类。

def quality_focal_loss(pred, target, beta=2.0):
    r"""Quality Focal Loss (QFL) is from `Generalized Focal Loss: Learning
    Qualified and Distributed Bounding Boxes for Dense Object Detection
    `_.

    Args:
        pred (torch.Tensor): Predicted joint representation of classification
            and quality (IoU) estimation with shape (N, C), C is the number of
            classes.
        target (tuple([torch.Tensor])): Target category label with shape (N,)
            and target quality label with shape (N,).
        beta (float): The beta parameter for calculating the modulating factor.
            Defaults to 2.0.

    Returns:
        torch.Tensor: Loss tensor with shape (N,).
    """
    assert len(target) == 2, """target for QFL must be a tuple of two elements,
        including category label and quality label, respectively"""
    # label denotes the category id, score denotes the quality score
    label, score = target

    # negatives are supervised by 0 quality score
    pred_sigmoid = pred.sigmoid()
    scale_factor = pred_sigmoid
    zerolabel = scale_factor.new_zeros(pred.shape)
    loss = F.binary_cross_entropy_with_logits(
        pred, zerolabel, reduction='none') * scale_factor.pow(beta)

    # FG cat_id: [0, num_classes -1], BG cat_id: num_classes
    bg_class_ind = pred.size(1)
    pos = ((label >= 0) & (label < bg_class_ind)).nonzero().squeeze(1)
    pos_label = label[pos].long()
    # positives are supervised by bbox quality (IoU) score
    scale_factor = score[pos] - pred_sigmoid[pos, pos_label]
    loss[pos, pos_label] = F.binary_cross_entropy_with_logits(
        pred[pos, pos_label], score[pos],
        reduction='none') * scale_factor.abs().pow(beta)

    loss = loss.sum(dim=1, keepdim=False)
    return loss

根据距离回归的一般分布离散积分得到实际学习到的距离偏差 

class Integral(nn.Module):
    """A fixed layer for calculating integral result from distribution.

    This layer calculates the target location by :math: `sum{P(y_i) * y_i}`,
    P(y_i) denotes the softmax vector that represents the discrete distribution
    y_i denotes the discrete set, usually {0, 1, 2, ..., reg_max}

    Args:
        reg_max (int): The maximal value of the discrete set. Default: 16. You
            may want to reset it according to your new dataset or related
            settings.
    """

    def __init__(self, reg_max=16):
        super(Integral, self).__init__()
        self.reg_max = reg_max
        self.register_buffer('project',
                             torch.linspace(0, self.reg_max, self.reg_max + 1))

    def forward(self, x):
        """Forward feature from the regression head to get integral result of
        bounding box location.

        Args:
            x (Tensor): Features of the regression head, shape (N, 4*(n+1)),
                n is self.reg_max.

        Returns:
            x (Tensor): Integral result of box locations, i.e., distance
                offsets from the box center in four directions, shape (N, 4).
        """
        x = F.softmax(x.reshape(-1, self.reg_max + 1), dim=1)  # (18,68)->(72,17)
        # x.sum(dim=1) 全等于1，共72个1
        x = F.linear(x, self.project.type_as(x)).reshape(-1, 4)  # (72,17)*(17)->(72)->(18,4)
        return x

除了QFL和DFL，实现还计算了GIoU Loss，最终的损失函数是这三个Loss的和。

实验

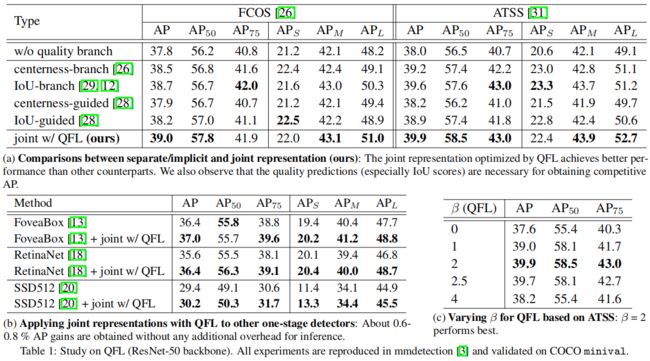
对于QFL，从下表(a)可以看出，本文提出的分类和定位质量联合表示结合QFL精度要优于其它质量估计表示。从表(b)可以看出，QFL在其它one-stage检测模型上也能提升精度。从表(c)可以看出，\(\beta=2\) 的精度最高。

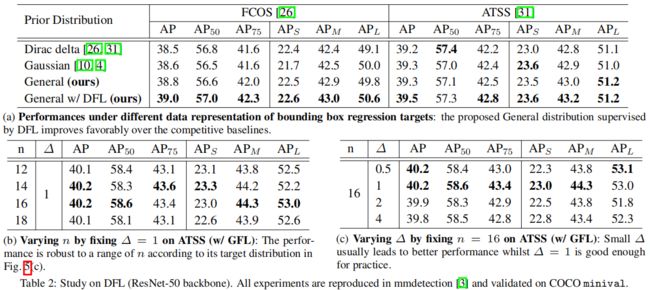
对于DFL，从下表(a)可以看出，本文提出的边框回归一般分布比狄拉克分布和高斯分布的效果都要好，结合DFL精度进一步得到提升。从下表(b)可以看出，ATSS中正样本个数 \(n\) 的选择对结果不敏感，取14或16时精度稍高一点。从下表(c)可以看出，一般分布区间间隔 \({\small \bigtriangleup } \) 小一点更好，文中取1。 

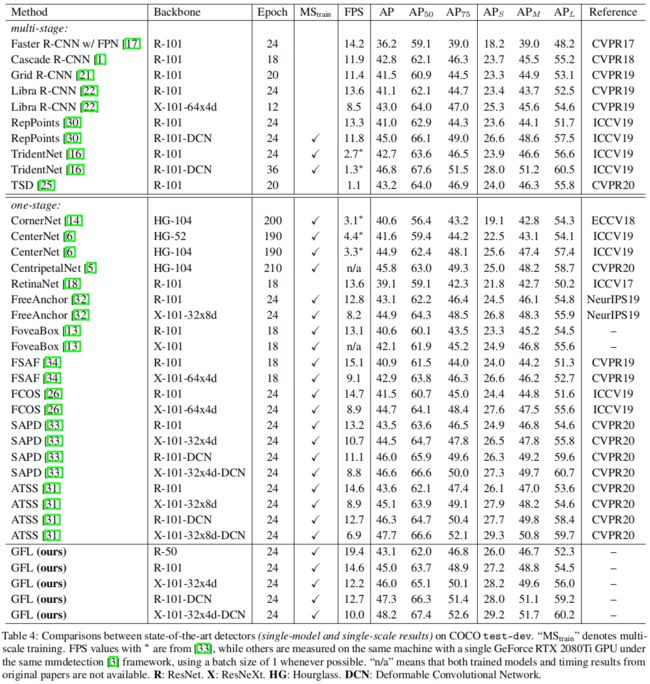
和其它模型的比较，从下表可以看出，在相同的backbone和训练配置下，GFL的精度都是最高的。 

参考

大白话 Generalized Focal Loss - 知乎

深入理解一下Generalized Focal Loss v1 & v2 - 知乎