基于项目的Top-N推荐算法（Item-Based Top-N Recommendation Algorithms，Mukund Deshpande and George Karypis，2004）

1 基本信息

项目	信息
名称	Item-Based Top-$N$ Recommendation Algorithms
作者	Mukund Deshpande，George Karypis
期刊	ACM Transactions on Information Systems (TOIS)
年份	2004
卷	22
期	1
页码	143—177
DOI	https://doi.org/10.1145/963770.963776
引用量	2930

---

2 研究和贡献

2.1 研究内容

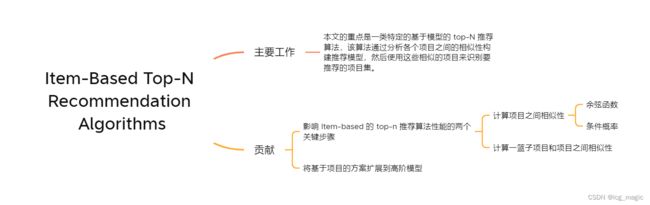
这篇文章的重点是一类特定的基于模型的 top-$N$ 推荐算法，该算法通过分析各个项目之间的相似性构建推荐模型，然后使用这些相似的项目来识别要推荐的项目集。

2.2 贡献

这篇文章的贡献分为两个部分。
第一个贡献，详细研究了影响基于项目的 top-$N$ 推荐算法性能的两个关键步骤。

• 第一步：用于计算项目之间相似性的方法。
• 第二步：用于组合这些相似性以计算一篮子项目和候选推荐项目之间的相似性的方法。

在第一步中，作者研究了两中不同计算项目–项目之间相似度的方法。第一个建模为用户空间中的向量，并使用余弦函数来测量相似度。另一个则使用基于两个项目之间的条件概率的技术来计算项目到项目的相似性。在第二步中，作者提出了一种组合这些相似性的方法，该方法解释了可能错误地偏向整体推荐的不同密度的项目邻域。

第二个贡献，是将这些基于项目的方案扩展到高阶模型，这些模型通过利用项目集之间的关系来获得最终推荐。作者提出了一类基于插值的高阶项目的 top-$N$ 推荐算法，该算法通过首先确定各种项目集–项目的相似性，然后将它们组合以确定用户的购物篮和候选推荐项目之间的相似性来构建推荐模型。

---

3 定义和符号

符号	含义
$n$	不同用户的数量（the number of distinct users）。
$m$	不同项目的数量（the number of distinct items）。
$N$	需要为特定用户计算的推荐数量。
customers	消费者，users 的同义词（synonym）。
products	产品，items 的同义词（synonym）。
dataset	有关不同用户已购买的物品的交易集。
$R$	用户–项目的二元矩阵，维度是 $n\times m$。
$R_{i,j}$	取值为 $\{0,1\}$。1 表示第 i 个消费者购买了第 j 个项目；否则为 0。
active user	想要为其计算 top-$N$ 推荐的用户。

定义1（top-$N$ 推荐问题）：给定用户–项目矩阵 $R$ 和一个用户已购买的项目集 $U$，识别有序项目集 $X$，满足 $\left|X\right|\le N$ 且 $X\cap U=\varnothing$。

---

4 算法

使用项目与项目相似度来计算不同项目之间相关性的一类基于模型的 top-$N$ 推荐算法。
这些算法背后的主要动机是一个消费者更倾向于购买和过去他/她曾经购买过的项目相似的项目。因此，通过分析历史购买信息，就可以自动识别这些相似项目的集合，并使用它们来形成 top-$N$ 推荐。

在高层次上，这些算法由两个不同的组件组成。第一个组件构建一个模型来捕获不同项目之间的相关性，第二个组件应用这个预先计算的模型来为活动用户获得 top-$N$ 推荐。

4.1 构建模型

算法流程（伪代码）如下图所示。

输入变量	含义
$R$	$n\times m$ 的用户–项目矩阵。
$k$	参数，它指定将为每个项目存储的项目到项目相似性的数量。

输出变量	含义
$\mathcal{M}$	模型本身，$m\times m$ 的矩阵，第 $j$ 列存储了和项目 $j$ 最相似的 $k$ 个项目。${\mathcal{M}}_{i,j}$ 的值表示项目 $j$ 和项目 $i$ 之间的相似度。

对于项目 $j$ 来说（$j$ 从 $1$ 变化到 $m$），分为两步：

1. 计算项目 $j$ 和其它项目 $i$ （$i$ 从 $1$ 变化到 $m$）的相似度。如果 $j=i$ 相等，表明是同一个项目，则自身相似度置为 0（因为为了找到相似度最高的项目，即最相似的项目）；否则，使用相似度公式计算相似度。公式为：
   $${\mathcal{M}}_{i,j}=\{\begin{array}{ll}\text{sim}(R_{\ast ,j},R_{\ast ,i}),& \text{if }i\ne j;\\ 0,& \text{otherwise}.\end{array}$$
2. 找出 ${\mathcal{M}}_{\ast ,j}$ 中（$\mathcal{M}$ 的第 $j$ 列）值最大的三个相似度，得到集合 ${\text{M}}_{\ast ,j}$。对于项目 $i$（$i$ 从 $1$ 变化到 $m$），重新对 ${\mathcal{M}}_{i,j}$ 进行赋值。如果 ${\mathcal{M}}_{i,j}$ 值不是最大的三个值之一，则置为 0。 公式为：
   $${\mathcal{M}}_{i,j}=\{\begin{array}{ll}{\mathcal{M}}_{i,j}=0,& \text{if }{M}_{i,j}\notin {\text{M}}_{\ast ,j};\\ {\mathcal{M}}_{i,j},& \text{otherwise}.\end{array}$$

$\mathcal{M}$ 对 $k$ 的参数化是出于对性能的考虑，它的选择代表了性能质量的权衡。

• 通过使用较小的 $k$ 值，可以确保 $\mathcal{M}$ 非常稀疏，因此即使在 $m$ 非常大的协同过滤环境和应用程序中也可以存储在主内存中。如果 $k$ 太小，那么结果模型将会包含有限的信息来构建推荐，因此可能会导致较低的质量。
• 实验表明 $k$ 的合理取值——$10<k<30$。较高的 $k$ 值会导致非常小的改善或没有改善。

4.1.1 项目之间的相似度度量

一般来说，两个项目 $i$ 和 $j$，如果有很多客户都购买了这两个项目，那么它们之间的相似度应该很高。
如果这样的客户很少，则应该很低。

还需要考虑两个不太明显的方面：

• 第一个与是否应该区分购买少量商品的客户和购买大量商品的客户有关。
  例如，考虑两个客户 $C_1$ 和 $C_2$，都购买了物品 $i$ 和 $j$，但是 $C_1$ 购买了 5 件额外的物品，而 $C_2$ 购买了 50 件额外的物品。在确定这对项目之间的相似性时，他们都购买了 $i$ 和 $j$ 的事实是否应该同等贡献？在某些情况下，来自购买较少商品的客户的共同购买信息比来自倾向于购买大量商品的客户的信息更可靠地指示两个共同购买的商品的相似性。
  实验表明，这种情况经常发生，并且能够将其考虑在内可以提高整体 top-$N$ 推荐性能。
• 第二个方面与一对项目之间的相似性是否应该是对称的有关。对称 $\text{sim}(i,j)=\text{sim}(j,i)$；不对称 $\text{sim}(i,j)\ne \text{sim}(j,i)$。当需要计算以截然不同的频率购买的成对物品之间的相似性时，通常会出现这个问题。
  例如，考虑两个物品 $i$ 和 $j$，使得 $i$ 的购买频率明显高于 $j$。由于频率不同，那么 $i$ 和 $j$ 共同购买的次数将会远比 $i$ 单独购买的次数小。$i$ 和 $j$ 之间的相似度应该怎样？站在 $i$ 的角度，它与 $j$ 的相似度很低，因为和 $j$ 共同发生占它发生的很小比例。然而，站在 $j$ 的角度，它与 $i$ 的相似度很高，因为和 $i$ 共同发生占它发生的很大比例。因此，如果使用非对称相似度方法，那么就会得到 $\text{sim}(i,j)<\text{sim}(j,i)$。
  对称相似度函数将倾向于消除对非常频繁的商品的推荐（这在很大程度上是显而易见的），因为只有当其他经常购买的商品在当前购物篮中时，这些商品才会被推荐。然而，在没有大多数客户经常购买的物品的数据集中，对称相似度函数将不必要地惩罚频率相对高于活跃用户当前购买的物品的物品的推荐。

4.1.1.1 基于余弦的相似性

基于余弦的相似度（cosine-based similarity），是一个对称相似度方法（symmetric）。
$R$ 是一个 $n\times m$ 用户–项目矩阵，项目 $i$ 和项目 $j$ 的相似度定义为对应于 $R$ 矩阵中第 $i$ 列和第 $j$ 列 $n$ 维向量的余弦。这些向量之间的余弦定义为：
$$\text{sim}(i,j)=\cos (R_{\ast ,i},R_{\ast ,j})=\frac{R_{\ast ,i}\cdot R_{\ast ,j}}{\Vert R_{\ast ,i}{\Vert }_2\Vert R_{\ast ,j}{\Vert }_2},\text{(1)}$$其中 “$\cdot$” 是向量的点击操作。

结果，经常购买的物品将倾向于与其他经常购买的物品相似，而不是与不经常购买的物品相似，反之亦然。在最简单的形式中，$R$ 的行可以对应于原始的二进制购买信息，在这种情况下，余弦相似度函数对购买少量和大量商品的客户一视同仁。但是，可以对每一行进行缩放，以便生成的基于余弦的相似度函数可以区分这些客户集。这可以通过将每一行缩放为单位长度（或任何其他范式）来完成。这种缩放的效果是，购买较少商品的客户将比购买更多商品的客户对等式中的点积贡献更高的权重。

4.1.1.2 基于条件概率的相似性

基于条件概率的相似性（conditional probability-based similarity），是一个非对称相似度方法（asymmetric）。
在已经购买的 $i$ 的情况下购买 $j$ 的条件概率 $P(j\mid i)$ 只不过是同时购买商品 $i$ 和 $j$ 的顾客数量除以购买 $i$ 的顾客总数，即
$$P(j\mid i)=\frac{\text{Freq}(ij)}{\text{Freq}(i)}.$$其中 $\text{Freq}(X)$ 是购买集合 $X$ 中商品的客户数量。记住，一般的，$P(j\mid i)\ne P(i\mid j)$。

如前所述，使用非对称相似度函数的一个限制是，每件商品 $i$ 都倾向于与经常购买的商品有较高的条件概率。这个问题可以通过将 $P(j\mid i)$ 除以一个取决于项目 $j$ 出现频率的量来纠正。已经提出了两种不同的方法来实现这一点。受信息检索系统中执行的逆文档频率缩放的启发，

• 第一点，将 $P(j\mid i)$ 乘以 ${\log }_2(P(j))$。
• 第二点，将 $P(j\mid i)$ 除以 $P(j)$。

实验表明，这种缩放极大地影响了推荐系统的性能，并且最佳缩放程度取决于问题。由于这些原因，文章使用以下公式来计算两个项目之间的相似度：
$$\text{sim}(i,j)=\frac{\text{Freq}(ij)}{\text{Freq}(i)\times (\text{Freq}(j){)}^{\alpha }},\text{(2)}$$其中 $\alpha$ 是取值为 0 到 1 之间的参数。当 $\alpha =0$ 时，就是 $P(j\mid i)$。当 $\alpha =1$ 时，它变得与 $P(j\mid i)$ 除以 $P(j)$ 的公式相似（直到一个比例因子）。
公式（2）的相似性方法没有区分购买不同数量项目的用户。为实现这种区分并赋予购买较少商品的客户更高的权重，通过以下方式扩展了公式（2）的相似性度量：首先将矩阵 $R$ 的每一行归一化为单位长度，然后定义物品 $i$ 和 $j$ 之间的相似度：
$$\text{sim}(i,j)=\frac{{\sum }_{\forall q:R_{q,j}>0}{R}_{q,j}}{\text{Freq}(i)\times (\text{Freq}(j){)}^{\alpha }}.\text{(3)}$$
公式（2）和公式（3）的区别是，取而代之使用在用户–项目矩阵第 $j$ 列的相应非零条目的总和，而不是使用共现频率。由于行被标准化为单位长度，购买更多商品的客户往往对整体相似性的贡献较小。这强调了购买较少商品的客户的购买决策。

4.2 应用模型

输入变量	含义
$\mathcal{M}$	模型。
$U$	存储活跃用户已购买项目的 $m\times 1$ 向量。向量 $U$ 中活跃用户的信息编码为如果用户购买了第 $i$ 个项目则设置$U_i=1$，否则设置为 0。
$N$	将要推荐的项目数量。

输出变量	含义
$x$	$m\times 1$ 向量，非零条目对应推荐的 top-$N$ 项目。

这些非零条目的权重表示推荐强度的度量，并且可以以非增加的推荐强度权重对各种推荐进行排序。在大多数情况下，$x$ 将恰好有 $N$ 个非零条目。然而，推荐的实际数量可能小于 $N$，因为它取决于用于构建 $\mathcal{M}$ 的 $k$ 的值以及活跃用户已经购买的商品数量。

向量 $x$ 分三步计算。

• 向量 $x$ 是通过将 $\mathcal{M}$ 与 $U$ 相乘来计算的（第 1 行）。$x$ 的非零项对应于活跃用户已经购买的每个项目最相似的 $k$ 个项目的并集，这些条目的权重不过是这些相似度的和。
• 将 $x$ 中对应于活跃用户已购买项目的条目置为 0。
• 将 $x$ 中小于最大的 $k$ 个值的条目都置为 0。

算法 4.2 的一个潜在缺点是每个项目 $j$ 与其 $k$ 个最相似的项目之间的原始相似性可能显著不同。也就是说，项目邻域具有不同的密度。对于不经常购买的物品尤其如此，因为与其他不经常购买的物品的适度重叠会导致相对较高的相似度值。因此，这些项目可以对 top-$N$ 项目的选择产生很大的影响，有时会导致错误的推荐。出于这个原因，文章不使用第 4.1.1 节中描述的各种方法计算的实际相似度，而是首先对每个项目 $j$ 进行归一化，使它们相加为 1。即 $\Vert {\mathcal{M}}_{\ast ,j}\Vert =1$，对于 $j=1,...,m$。正如实验所示，这总是可以提高 top-N 推荐质量。

4.3 计算复杂度

对于每一个项目，需要计算其与 $R$ 中的其它项目之间的相似性，那么需要计算 $(m-1)$ 次。所有的项目与项目之间的相似性，则总计需要计算 $m(m-1)$ 次。计算一个项目与另一个项目之间的相似性，时间复杂度为 $O(n)$。所以模型构建这一步的复杂度上限为 $O(m^{2}n)$。实际复杂度要显著小于这个复杂度，因为相似度矩阵是极其稀疏的。
最后为每一个已购买 $q$ 个项目的活跃用户计算 top-$N$ 推荐的时间为 $O(kq)$，因为需要访问用户已购买的每一个项目的 $k$ 个最相似的项目，并识别出总体上 $N$ 个最相似的物品。

---

5 基于高阶项目的 TOP-N 推荐算法

到目前为止，文章的讨论主要集中在基于项目的 top-$N$ 推荐算法上，其中推荐是通过考虑项目对（pairs of item）之间的关系来计算的，也就是说，对于活动用户篮子中的每个项目，确定相似的项目并且这些相似的被聚合以获得所需的 top-$N$ 推荐。
为了解决这个问题，文章开发了基于项目的 top-$N$ 推荐方案，在确定要推荐给用户的项目集时，使用项目的所有组合（即项目集）直到特定大小 $l$。

5.1 构建模型

算法 5.1 计算了 $l$ 个不同的模型矩阵 ${\mathcal{M}}^1$、${\mathcal{M}}^2$、$\dots$、${\mathcal{M}}^l$，大小分别是 $m\times m$、$m\times m^2$、$\dots$、$m\times m^l$。对于 $r$ 的一个特定值，${\mathcal{M}}^r$ 是通过生成 $r$ 个项目的所有可能组合来构建 $\{q_1,q_2,\dots ,q_r\}$（行 1 的循环），计算这些集合与数据集中所有其他 $m$ 个项目之间的相似性（行 2 的循环），其中仅保留${\mathcal{M}}^r$ 对应列中的 $k$ 个最大相似度。

输入变量	含义
$R$	用户–项目购买矩阵。
$l$	阶数。
$k$	最大相似度的数目。

输出变量	含义
${\mathcal{M}}^1,{\mathcal{M}}^2,\dots ,{\mathcal{M}}^l$	模型矩阵。

$个人理解$
第一个循环（行 1）我也没看懂，不知道怎么计算的，猜测大概是求了一个集合。这里利用计算来验证一下，顺便理解一下这个循环的功能。这里假设 $l=2$，$m=10$。

$r=1$	$j\in [1..10^1]$	$i\in [1..1]$	$q_i\leftarrow \left((j\mathrm{m}\mathrm{o}\mathrm{d}{m}^{r-i+1})\mathrm{div}{m}^{r-i}\right)+1$
1	1	1	$q_1=\left((1\mathrm{m}\mathrm{o}\mathrm{d}10^1)\mathrm{div}10^0\right)+1=2$
1	2	1	$q_1=\left((2\mathrm{m}\mathrm{o}\mathrm{d}10^1)\mathrm{div}10^0\right)+1=3$
$\dots$	$\dots$	$\dots$	$\dots$
1	9	1	$q_1=\left((9\mathrm{m}\mathrm{o}\mathrm{d}100^1)\mathrm{div}10^0\right)+1=10$
1	10	1	$q_1=\left((10\mathrm{m}\mathrm{o}\mathrm{d}100^1)\mathrm{div}10^0\right)+1=1$

$r=2$	$j\in [1..10^2]$	$i\in [1..2]$	$q_i\leftarrow \left((j\mathrm{m}\mathrm{o}\mathrm{d}{m}^{r-i+1})\mathrm{div}{m}^{r-i}\right)+1$
2	1	1	$q_1=\left((1\mathrm{m}\mathrm{o}\mathrm{d}10^2)\mathrm{div}10^1\right)+1=1$
2	1	2	$q_2=\left((1\mathrm{m}\mathrm{o}\mathrm{d}10^1)\mathrm{div}10^0\right)+1=2$
2	2	1	$q_1=\left((2\mathrm{m}\mathrm{o}\mathrm{d}10^2)\mathrm{div}10^1\right)+1=1$
2	2	2	$q_2=\left((2\mathrm{m}\mathrm{o}\mathrm{d}10^1)\mathrm{div}10^0\right)+1=3$
$\dots$	$\dots$	$\dots$	$\dots$
2	99	1	$q_1=\left((99\mathrm{m}\mathrm{o}\mathrm{d}10^2)\mathrm{div}10^1\right)+1=10$
2	99	2	$q_2=\left((99\mathrm{m}\mathrm{o}\mathrm{d}10^1)\mathrm{div}10^0\right)+1=10$
2	100	1	$q_1=\left((100\mathrm{m}\mathrm{o}\mathrm{d}10^2)\mathrm{div}10^1\right)+1=1$
2	100	2	$q_2=\left((100\mathrm{m}\mathrm{o}\mathrm{d}10^1)\mathrm{div}10^0\right)+1=1$

循环 2 的功能是遍历所有的项目 $i$，计算 $i$ 与 $r$ 阶下第 $j$ 个项目集 $\{q_1,\dots ,q_r\}$ 之间的相似度 ${\mathcal{M}}_{i,j}^r$。如果 $i$ 是 $\{q_1,\dots ,q_r\}$ 中的一员，那么相似度置为 0。如果不是，那么使用相似度计算公式获得。

举两个例子

当 $r=1$，$j=1$：
循环 1 得到的结果为 $q_1=2$，那么 $\{q_1,\dots ,q_r\}=\{q_1\}=\{2\}$，这个就是选择好的项目集。
循环 2，$i$ 从 1 变化到 $m$。当 $i\in \{2\}$ 时，即 $i$ 在项目集中，此时置 ${\mathcal{M}}_{j,j}=0$。当 $i\notin \{2\}$ 时，即 $i$ 不在项目集中，此时计算第 $i$ 个项目的购买数据 $R_{\ast ,i}$ 与项目集的购买数据 $\{R_{\ast ,2}\}$ 之间的相似度，并将其赋值给 ${\mathcal{M}}_{i,j}^1$。所以出现一个 ${\mathcal{M}}_{j,j}$ 是什么操作？

$i$	$i\in \{q_1,\dots ,q_r\}$	${\mathcal{M}}_{i,j}^r\mathrm{or}{\mathcal{M}}_{j,j}$
1	False	${\mathcal{M}}_{1,1}^1=\mathrm{sim}(\{R_{\ast ,2}\},R_{\ast ,1})$
2	True	${\mathcal{M}}_{1,1}=0$
$\dots$	$\dots$	$\dots$
9	False	${\mathcal{M}}_{9,1}^1=\mathrm{sim}(\{R_{\ast ,2}\},R_{\ast ,9})$
10	False	${\mathcal{M}}_{10,1}^1=\mathrm{sim}(\{R_{\ast ,2}\},R_{\ast ,10})$

所以我严重怀疑论文循环 2 写错了。
接下来，让我求证一下
当 $r=2$，$j=98$：
循环 1 得到的结果为 $q_1=10,q_2=9$，那么 $\{q_1,q_2,\dots ,q_r\}=\{10,9\}$，这就是选择好的项目集。

$i$	$i\in \{q_1,\dots ,q_r\}$	${\mathcal{M}}_{i,j}^r\mathrm{or}{\mathcal{M}}_{j,j}$
1	False	${\mathcal{M}}_{1,98}^2=\mathrm{sim}(\{R_{\ast ,10},R_{\ast ,9}\},R_{\ast ,1})$
$\dots$	$\dots$	$\dots$
9	True	${\mathcal{M}}_{98,98}=0$
10	True	${\mathcal{M}}_{98,98}=0$

前文提到 ${\mathcal{M}}^r$ 的维度为 $m\times m^r$。这里 ${\mathcal{M}}^2$ 的维度为 $98\ast 98$，而 $m=10$，正确维度应该为 $10\times 10^2$。所以已经能确定图中的算法循环 2 是错误的。进一步地，循环 2 中出现了 $\mathcal{M}$，这个变量（矩阵）在算法中并没有使用。无用的变量拿来干嘛？？？那么有没有可能 $\mathcal{M}$ 表示 $r=1$ 时的相似度矩阵呢？答案是：也不可能！因为算法最后一句返回了 ${\mathcal{M}}^1$，说明当 $r=1$ 时，相似度是用 ${\mathcal{M}}^1$ 表示的。
综上两点可知，循环 2 是确实有误的。

$经过上面的分析，循环2是错误的，正确形式为：$
$${\mathcal{M}}_{i,j}^r=\{\begin{array}{ll}\mathrm{sim}(\{R_{\ast ,q_1},\dots ,R_{\ast ,q_r}\},R_{\ast ,i}),& \text{if }i\notin \{q_1,\dots ,q_r\};\\ 0,& \text{otherwise}.\end{array}$$

经过修改后，算法的循环 2 就正确表达了论文作者的意图。（PS：但是循环 1 还存在问题，这里不再讨论。）

修改后的循环 1 和循环 2 的例子
当 $r=1$，$j=1$：
循环 1 得到的结果为 $q_1=2$，那么 $\{q_1,\dots ,q_r\}=\{q_1\}=\{2\}$，这个就是选择好的项目集。
循环 2，$i$ 从 1 变化到 $m$。当 $i\in \{2\}$ 时，即 $i$ 在项目集中，自身与自身的相似度置为 0，此时置 ${\mathcal{M}}_{i,1}^1=0$。当 $i\notin \{2\}$ 时，即 $i$ 不在项目集中，此时计算第 $i$ 个项目的购买数据 $R_{\ast ,i}$ 与项目集的购买数据 $\{R_{\ast ,2}\}$ 之间的相似度，并将其赋值给 ${\mathcal{M}}_{i,1}^1$。

$i$	$i\in \{2\}$	${\mathcal{M}}_{i,1}^1=\mathrm{sim}(\{R_{\ast ,2}\},R_{\ast ,i})$
1	False	${\mathcal{M}}_{1,1}^1=\mathrm{sim}(\{R_{\ast ,2}\},R_{\ast ,1})$
2	True	${\mathcal{M}}_{2,1}^1=0$
$\dots$	$\dots$	$\dots$
9	False	${\mathcal{M}}_{9,1}^1=\mathrm{sim}(\{R_{\ast ,2}\},R_{\ast ,9})$
10	False	${\mathcal{M}}_{10,1}^1=\mathrm{sim}(\{R_{\ast ,2}\},R_{\ast ,10})$

当 $r=2$，$j=98$：
循环 1 得到的结果为 $q_1=10,q_2=9$，那么 $\{q_1,q_2,\dots ,q_r\}=\{10,9\}$，这就是选择好的项目集。
循环 2，$i$ 从 1 变化到 $m$。当 $i\in \{9,10\}$ 时，即 $i$ 在项目集中，自身与自身的相似度置为 0，此时置 ${\mathcal{M}}_{i,98}^2=0$。当 $i\notin \{9,10\}$ 时，即 $i$ 不在项目集中，此时计算第 $i$ 个项目的购买数据 $R_{\ast ,i}$ 与项目集的购买数据 $\{R_{\ast ,9},R_{\ast ,10}\}$ 之间的相似度，并将其赋值给 ${\mathcal{M}}_{i,98}^2$。

$i$	$i\in \{9,10\}$	${\mathcal{M}}_{i,98}^2=\mathrm{sim}(\{R_{\ast ,9},R_{\ast ,10}\},R_{\ast ,i})$
1	False	${\mathcal{M}}_{1,98}^2=\mathrm{sim}(\{R_{\ast ,10},R_{\ast ,9}\},R_{\ast ,1})$
$\dots$	$\dots$	$\dots$
9	True	${\mathcal{M}}_{9,98}^2=0$
10	True	${\mathcal{M}}_{10,98}^2=0$

算法 5.1 分析：

• 循环 1 得到 $r$ 阶下第 $j$ 个项目集，模为 $r$。
• 循环 2 计算其他 $(m-r)$ 个项目与项目集的相似度。
• 循环 3 从 $(m-r)$ 个非零相似度的项目中，保留相似度最大的 $k$ 个项目，将剩余的 $(m-r-k)$ 个项目置为 0。
• 最后返回 1 阶相似度矩阵 ${\mathcal{M}}^1$、2 阶相似度矩阵 ${\mathcal{M}}^2$、……、$l$ 阶相似度矩阵 ${\mathcal{M}}^l$。

5.1.1 项目集–项目相似度

基于余弦的方法。首先构造一个 $v$。$v$ 是一个 $n$ 元向量，
$$v(i)=\{\begin{array}{ll}0,& \text{if at least one of the }{R}_{i,q_j}=0\text{ for }j=1,2,\dots ,r;\\ \sum _{j=1}^r\frac{R_{i,q_j}}{\Vert R_{\ast ,q_j}{\Vert }_2},& \text{otherwise}.\end{array}$$
本质上，$v$ 是项目集中项目的单个单位长度归一化项目向量的总和，并添加了约束，即如果矩阵的特定行不包含所有 $r$ 个项目，它将被设置为零。
此时项目集 $\{q_1,q_2,\dots ,q_r\}$ 用 $v$ 表示。项目集 $\{q_1,q_2,\dots ,q_r\}$ 和其他项目 $u$ 之间的相似度，就变成了 $v$ 与 $u$ 之间的相似度，直接使用公式（1）。

基于条件概率的方法。相似度计算则使用和公式（3）相似的公式，如下所示：
$$\mathrm{sim}(\{q_1,q_2,\dots ,q_r\},u)=\frac{{\sum }_{\forall i:R_{i,q_j}>0,\text{for }j=1,2,\dots ,r}{R}_{i,q_1}}{\mathrm{Freq}(\left\{q_1,q_2,\dots ,q_r\right\})\times {\left(\mathrm{Freq}(u)\right)}^{\alpha }},\text{(4)}$$其中 $\mathrm{Freq}(\left\{q_1,q_2,\dots ,q_r\right\})$ 是矩阵中包含项目集中所有项目的行数量。此外，由于用户–项目矩阵 $R$ 的行已被归一化为单位长度，$R_{i,q_1}=R_{i,q_2}=\cdots =R_{i,q_r}$。

5.2 应用模型

算法 5.2 展示了为活跃用户进行 top-$N$ 推荐的计算，其中 ${\mathcal{M}}^1,{\mathcal{M}}^2,\dots ,{\mathcal{M}}^l$ 是不同的模型矩阵，$U$ 是一个存储用户已购买项目的 $m\times 1$ 向量，$N$ 是将被推荐的项目数。$U$ 的格式和返回向量的格式与早期的项目–项目相似度算法使用的格式相同（算法 4.2）。

输入变量	含义
${\mathcal{M}}^1,{\mathcal{M}}^2,\dots ,{\mathcal{M}}^l$	不同的模型矩阵。
$U$	用户已购买项目的 $m\times 1$ 向量。
$N$	将被推荐的项目数。

输出变量	含义
$x$	推荐列表。

循环 1 生成 $l$ 个不同的向量 $U^1$、$U^2$、……、$U^l$，大小分别是 $m\times 1$、$m^2\times 1$、……、$m^l\times 1$。对于 $r$ 的一个特定值，$U^r$ 通过生成 $r$ 个项目 $\{q_1,q_2,\dots ,q_r\}$ 的每个可能组合来构建。如果活跃用户购买了所有的这些项目，则设置 $U^r$ 相应条目设置为 1，否则设置为 0。第 2 行，每个项目集的行索引 $j$ 的构造使其与用于填充相应 ${\mathcal{M}}^r$ 矩阵的相同项目集的列索引相同。$x$ 是 ${\mathcal{M}}^r$ 和 $U^r$ 对矩阵–向量乘积的结果。循环 3 将活跃用户已购买的项目剔除，也就是将 $x$ 中对应的条目置为 0。循环 4 保留 $x$ 中 $N$ 个最相似的项目。

5.3 实际考虑

存在的问题：

• 随着模型的阶数，计算呈现指数级增长。
• 很多项目集的发生频数要么为 0 要么非常小。

基于以上考虑，文章仅适用于在用户–项目矩阵 $R$ 中出现足够多次数的项目集。使用计算高效的算法，寻找一个大小为 $l$ 且出现在 $\sigma \%$ 的行中的所有频繁项集，并仅针对这些频繁项集计算 $k$ 个最相似的其他项目。

（说实话，看到这里，我已经不知道作者是怎么解决的了！！！）

---

6 实验

略——后面有时间再慢慢补充……

---

参考

1. Deshpande Mukund, and George Karypis. “Item-based top-n recommendation algorithms.” ACM Transactions on Information Systems (TOIS) 22.1 (2004): 143-177.

---

修改记录

时间	内容
2022年5月17日20:35:56	“在”→“再”