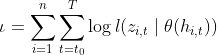DeepAR技术:论文笔记
Introduction
目前,预测技术(Forecasting)逐渐在商业领域和数据驱动决策方面的自动化和最优化成为首选工具。最近几年,随着数据越来越庞大,一个新的问题逐渐浮出水面:大规模的时序数据(time-series data)逐渐取代小规模时序数据。而预测这类型大数据的关键在于获取相关的时序信息。而此篇文章,针对相关问题,作者提出了基于自回归循环神经网络(autoregressive recurrent network)的DeepAR技术。
该技术的进步之处在于以下四点:
1)由于该模型学习的是周期性的表现(seasonal behavior)并且是基于贯穿时间序列的协变量(covariaties),在获取高复杂度、组依赖的表现时,仅有少量的数据处理需要手动进行。
2)该技术使蒙特卡洛样本形式的概率预测可以在预测的范围内,被用来对所有的子范围进行一致性分位数检验。
3)通过学习相似的数据,该模型可以被用来进行对仅有一点历史数据或者根本没有历史数据的项目预测。
4)实现该模型的方法不是一定通过高斯噪声,其他概率函数也是可行的,这取决于使用者的具体情况。
Related work
此处略过,内容大致为近年来在时序数据预测上,神经网络的发展和遇到的问题总结。具体情况可参考原文。
Model
1、先做一些符号说明:①时序数据 ![]() 在时间
在时间 ![]() 的值表示为 。
的值表示为 。
②时序![]() ,
, ![]() 表示我们未知其值的最早时间点,即预
表示我们未知其值的最早时间点,即预
要预测序列的起点。
③文中将![]() 分别称为条件区间和预测区间。
分别称为条件区间和预测区间。
④表示在整个时间序列的时间节点上都已知的协变量。
2、目标:将条件分布 模型化,如下图所示,为模型概略图
![]()
模型梗概: 训练部分(左半部分):在每一个时间节点![]() ,网络的输入是协变量 , 目标值的前一个值 , 以及上一次网络的输出 。 网络的输出 之后将被用来计算似然函数
,网络的输入是协变量 , 目标值的前一个值 , 以及上一次网络的输出 。 网络的输出 之后将被用来计算似然函数![]() 用做输入的参数 ,而这个函数将被用来训练网络。在预测时,时间序列的符合
用做输入的参数 ,而这个函数将被用来训练网络。在预测时,时间序列的符合![]() 历史数据将被输入。在预测部分(右半部分):对于
历史数据将被输入。在预测部分(右半部分):对于![]() 的样本, 这些样本会被提取出来并且被反馈为下一个节点的输出区间,该过程重复直到区间
的样本, 这些样本会被提取出来并且被反馈为下一个节点的输出区间,该过程重复直到区间![]() 的最后,并且得到一个最终输出结果。(模型示意图中,虽然左右两边输入输出的时间下标相同,但都是宏观的表示,实际应用中训练过程用条件区间的的数据,预测过程用预测区间的数据,二者无交集)
的最后,并且得到一个最终输出结果。(模型示意图中,虽然左右两边输入输出的时间下标相同,但都是宏观的表示,实际应用中训练过程用条件区间的的数据,预测过程用预测区间的数据,二者无交集)
3、详细内容(这部分可以尝试理解,大部分的计算都是神经网络内部完成):
①规定整个模型的分布是被输出参数化的似然函数因子的乘积,即:
其中
(1)
,![]() 是LSTM神经网络神经元内部构成的函数、似然函数是一个固定分布,它的参数由神经网络的输出和函数给出(下面说明)
是LSTM神经网络神经元内部构成的函数、似然函数是一个固定分布,它的参数由神经网络的输出和函数给出(下面说明)
②条件区间的值经过初始的输出状态(此输出状态为编码网络的输出)转化为预测区间。总体来说,这个编码网络可以有不同的结构,在本实验中,作者则在条件区间和预测区间使用了同一种网络,目的是在序列预测序列的模型中,编码器和解码器相匹配)。 进一步来说,我们设置编码器和解码器之间,编码器的最终参数要传递给解码器,并作为解码器的初始参数。这样则可以通过(1)和编码器的最终输出状态 。编码器的初始状态和用0来初始化。
③给出模型的参数![]() ,我们可以直接通过原始采样法(ancestral sampling)获得联合样本 :
,我们可以直接通过原始采样法(ancestral sampling)获得联合样本 :
1)首先,通过(1)对时序![]() 来计算
来计算
2)再对时序![]() 计算,其中用以及来初始化
计算,其中用以及来初始化
④likelihood model (这里是需要我们对于网络做一些手工调整的部分):
1)似然函数![]() 决定“噪声模型”(noise model)。它应该选择最符合数据统计属性的似然函数。在模型工作的过程中,网络直接预测下个时间节点概率分布的所有参数
决定“噪声模型”(noise model)。它应该选择最符合数据统计属性的似然函数。在模型工作的过程中,网络直接预测下个时间节点概率分布的所有参数![]() 。
。
2)在这篇文章的实验工作中,作者考虑了两种选择:对于真实数值数据,选择高斯似然(Gaussian likelihood);对于正技术数据(positive count data),选择负二项分布(negative-binominal)。 其他的似然模型也可以应用到这里面,例如对于二分类数据,选择伯努利分布;单元分割数据选择beta分布(beta likelihood),当然,对于处理复杂的边缘数据,也可以混合使用各种分布函数,但要保证这个分布的样本可以被比较简单地获得。
3)作者使用数学期望(mean)和标准差(standard deviation)来将高斯分布参数化,即![]() ,其中期望
,其中期望![]() 由网络输出的仿射变换函数(affine funciton)给出,而
由网络输出的仿射变换函数(affine funciton)给出,而![]() 由跟随着softplus激活函数的仿射变换得到,目的在于保证方差大于0 。其中
由跟随着softplus激活函数的仿射变换得到,目的在于保证方差大于0 。其中
![]()
4)这里的仿射变换函数实际上就是全连接层的输出的计算,假设![]() 中,H表示后面跟随一个非线性激活函数的仿射变换,y的实际计算方式是
中,H表示后面跟随一个非线性激活函数的仿射变换,y的实际计算方式是![]() 与该层的权重矩阵的叉乘的结果与偏移量相加,
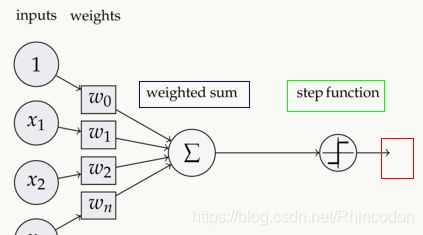
与该层的权重矩阵的叉乘的结果与偏移量相加,![]() 为输入向量,也就是说,这里的仿射变换函数的结果是最终激活函数的输入。具体见下图:
为输入向量,也就是说,这里的仿射变换函数的结果是最终激活函数的输入。具体见下图:
其中蓝框的weighted sum即为仿射变换函数,它的输出就是![]() ;绿框就是softplus函数,红框表示最终输出,结果就是
;绿框就是softplus函数,红框表示最终输出,结果就是![]() 。
。
5)其他分布函数的参数提取可参照原文,在此不做过多赘述。
⑤Training:
1)给定一个在预测区间已知的时间区间,从中获得时序的数据和有关的协变量。参数![]() 由RNN的参数
由RNN的参数![]() 和参数
和参数![]() 组成,而
组成,而![]() 可有最大对数似然估计获得(maximizing the log-likelihood):
可有最大对数似然估计获得(maximizing the log-likelihood):
由于是已经确定的对于网络输入的函数,所以计算(2)所需要的所有值已知,并且(2)可以通过计算![]() 的梯度直接被随机梯度下降算法优化
的梯度直接被随机梯度下降算法优化