⭐本专栏针对FPGA进行入门学习,从数电中常见的逻辑代数讲起,结合Verilog HDL语言学习与仿真,主要对组合逻辑电路与时序逻辑电路进行分析与设计,对状态机FSM进行剖析与建模。
文章和代码已归档至【Github仓库:hardware-tutorial】,需要的朋友们自取。或者关注公众号【AIShareLab】,回复 FPGA 也可获取。
D触发器的逻辑功能
D触发器的逻辑符号
![]()
把 CP 有效沿到来之前电路的状态称为现态,用$Q^n$表示。
把 CP 有效沿到来之后,电路所进入的新状态称为次态,用$Q^{n+1}$表示。
特性表
| D | $Q^n$ | $Q^{n+1}$ |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
特性方程
$$ Q^{n+1} = D $$
状态图
![]()
有清零输入和预置输入的D 触发器
由于直接置1和清零时跟CP信号无关,所以称置1、清零操作是异步置1和异步清零。
![]()
直接置1和直接清零的过程如下:
(1) 当 $\bar{S}_{D}=0$, $\bar{R}_{D}=1$ 时, 使得 $Y_{1}=1$ , $\bar{S}=\overline{Y_{1} \cdot C P \cdot \bar{R}_{D}}=\overline{C P}$, $\quad \bar{R}=\overline{\bar{S} \cdot C P \cdot Y_{4}}=1$ ,于是 $Q=1$, $\bar{Q}=0$ , 即将输出 Q 直接置 1 。
(2) 当 $\bar{S}_{\mathrm{D}}=1$, $\bar{R}_{\mathrm{D}}=0$ 时, 使得 $\bar{S}=1$ , 于是 $Q=0$, $\bar{Q}=1$ , 即将输出 Q 直接清零。
![]()
有同步清零端的 D 触发器
所谓同步清零是指在清零输入信号有效,并且CP的有效边沿(如上升沿)到来时,才能将触发器清零。
(a) 实现同步清零的方案之一
(b) 实现同步清零的方案之二
![]()
有使能端的D触发器
功能:
- En=0,Q 保持不变。
- En=1,在CP作用下,Q = D。
![]()
![]()
$$ Q^{n+1}=\overline{C E} \cdot Q^{n}+C E \cdot D $$
逻辑符号
D3触发器及其应用电路的Verilog HDL建模
例1.试对图所示的带有异步清零和异步置位的边沿D触发器进行建模。
![]()
有异步输入端的D触发器
//版本1:
module Set_Rst_DFF (Q, Q_, D, CP, Rd_, Sd_);
output Q,Q_;
input D,CP,Rd_,Sd_;
wire Y1,Y2,Y3,Y4,Y5,Y6;
assign #5 Y1 = ~(Sd_ & Y2 & Y4);
assign #5 Y2 = ~(Rd_ & CP & Y1);
assign #5 Y3 = ~(CP & Y2 & Y4);
assign #5 Y4 = ~(Rd_ & Y3 & D );
assign #5 Y5 = ~(Sd_ & Y2 & Y6);
assign #5 Y6 = ~(Rd_ & Y3 & Y5);
assign Q = Y5;
assign Q_= Y6;
endmodule版本1: 根据该图使用连续赋值语句来建模,在assign语句中的#5表示给每个与非门加5个单位时间的传输延迟。
//版本2
module Set_Rst_DFF_bh (Q, Q_, D, CP, Rd_, Sd_);
output reg Q;
output Q_;
input D,CP,Rd_,Sd_;
assign Q_= ~Q;
always @(posedge CP or negedge Sd_ or negedge Rd_)
if (~Sd_) //等同于: if (Sd_== 0)
Q <= 1'b1;
else if (~Rd_)
Q <= 1'b0;
else
Q <= D;
endmodule版本2的特点:
采用功能描述风格,使用always和if-else对输出变量赋值。
negedge Sd_是一个异步事件,它与if(~Sd_)必须匹配,negedge Rd_是另一个异步事件,它与if(~Rd_)必须匹配,这是语法规定。
- 当
Sd_为0时,将输出Q置1; - 当
Sd_=1且Rd_=0时,将输出Q置0; - 当
Sd_和Rd_均不为0,且时钟CP的上升沿到来时,将输入D传给输出Q。
注意,如果置1事件、置0事件和时钟事件同时发生,则置1事件的优先级别最高、置0事件的次之,时钟事件的优先级最低。
例2 具有同步清零功能的上升沿D触发器。
![]()
![]()
module Sync_rst_DFF (Q, D, CP, Rd_);
output reg Q;
input D, CP, Rd_;
always @(posedge CP)
if ( !Rd_) // also as (~Rd_)
Q <= 0;
else
Q <= D;
endmodule例4 试用功能描述风格对图所示电路进行建模(2分频电路) ,并给出仿真结果。
解:(1)设计块:使用always和if-else语句对输出变量赋值,其代码如下。
![]()
`timescale 1 ns/ 1 ns
module _2Divider (Q,CP,Rd_);
output reg Q;
input CP,Rd_;
wire D;
assign D = ~Q;
always @(posedge CP or
negedge Rd_)
if(~Rd_) Q <= 1'b0;
else Q <= D;
endmodule(2)激励块:给输入变量赋值。
`timescale 1 ns/ 1 ns
module test_2Divider();
reg CP, Rd_; wire Q;
//调用(例化)设计块
_2Divider U1 ( .CP(CP), .Q(Q),.Rd_(Rd_) );
initial begin //产生复位信号Rd_
Rd_ = 1'b0;
Rd_ = #2000 1'b1;
#8000 $stop;
end
always begin //产生时钟信号CP
CP = 1'b0;
CP = #500 1'b1;
#500;
end
endmodule(3)仿真波形(用ModelSim)
由图可知,时钟CP的周期为1000ns,在2000ns之前,清零信号Rd_有效,输出Q被清零。在此之后,Rd_=1,在2500ns时,CP上升沿到来,Q=1;到下一个CP上升沿(3500ns)时,Q=0,再到下一个CP上升沿(4500ns)时,Q=1,……,如此重复,直到8000ns时,系统任务$stop被执行,仿真停止。
总之,在不考虑清零信号Rd_的作用时,每当CP上升沿到来时,触发器状态Q翻转一次。输出信号Q的频率正好是CP频率的二分之一,故称该电路为2分频电路。所谓分频电路,是指可将输入的高频信号变为低频信号输出的电路。
例5 试对图所示电路进行建模,并给出仿真结果。
4位异步二进制计数器逻辑图
![]()
解:(1)设计块:采用结构描述风格的代码如下。编写了两个模块,这两个模块可以放在一个文件中,文件名为Ripplecounter.v。
第一个主模块Ripplecounter作为设计的顶层,它实例引用分频器子模块_2Divider1共4次,第二个分频器子模块_2Divider1作为设计的底层。
`timescale 1 ns/ 1 ns
/*==== 设计块:Ripplecounter.v ====*/
module Ripplecounter (Q,CP,CLR_);
output [3:0] Q;
input CP, CLR_;
//实例引用分频器模块 _2Divider1
_2Divider1 FF0 (Q[0],CP ,CLR_);
//注意, 引用时端口的排列顺序--位置关联
_2Divider1 FF1 (Q[1],~Q[0],CLR_);
_2Divider1 FF2 (Q[2],~Q[1],CLR_);
_2Divider1 FF3 (Q[3],~Q[2],CLR_);
endmodule 设计的底层模块 _2Divider1
//分频器子模块
module _2Divider1 (Q,CP,Rd_);
output reg Q;
input CP,Rd_;
always @(posedge CP or negedge Rd_)
if(!Rd_)
Q <= 1'b0;
else
Q <= ~Q;
endmodule (2)激励块:给输入变量(CLR_和CP)赋值。
/*==== 激励块:test_Ripplecounter.v ====*/
module test_Ripplecounter();
reg CLR_, CP;
wire [3:0] Q;
Ripplecounter i1 (.CLR_(CLR_),.CP(CP),.Q(Q));
initial begin // CLR_
CLR_ = 1'b0;
CLR_ = #20 1'b1;
#400 $stop;
end
always begin // CP
CP = 1'b0;
CP = #10 1'b1;
#10;
end
endmodule(3)仿真波形:如下图所示。
![]()
由图可知,
- 时钟CP的周期为20ns。
- 开始时,清零信号CLR_有效(0~20ns),输出Q被清零。
- 20ns之后,CLR_一直为高电平,
- 在30ns时,CP上升沿到来, Q=0001;到下一个CP上升沿(50ns)时,Q=0010,
- 再到下一个CP上升沿(70ns)时,Q=0011,……,如此重复,到310ns时,Q=1111,
- 到330ns时,Q=0000,……,直到系统任务$stop被执行,仿真停止。
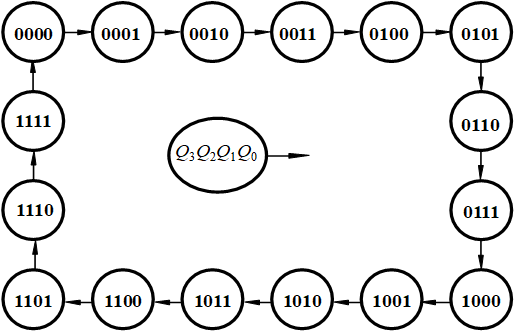
电路首先在CLR_的作用下,输出被清零。此后当CLR_=1时,每当CP上升沿到来时,电路状态Q就在原来二进制值的基础上增加1,即符合二进制递增计数的规律,直到计数值为1111时,再来一个CP上升沿,计数值回到0000,重新开始计数。故称该电路为4位二进制递增计数器(Ripplecounter:纹波计数器) 。
可见,计数器实际上是对时钟脉冲进行计数,每到来一个时钟脉冲触发沿,计数器改变一次状态。
参考文献:
- Verilog HDL与FPGA数字系统设计,罗杰,机械工业出版社,2015年04月
- Verilog HDL与CPLD/FPGA项目开发教程(第2版), 聂章龙, 机械工业出版社, 2015年12月
- Verilog HDL数字设计与综合(第2版), Samir Palnitkar著,夏宇闻等译, 电子工业出版社, 2015年08月
- Verilog HDL入门(第3版), J. BHASKER 著 夏宇闻甘伟 译, 北京航空航天大学出版社, 2019年03月
欢迎关注公众号【AIShareLab】,一起交流更多相关知识,前沿算法,Paper解读,项目源码,面经总结。