从逻辑回归推广到广义线性模型

1.引言

前几天突然想复习一下逻辑回归算法，于是在网上搜了一些大神写的博客，收获很多，也让我想起之前看过Andrew Ng的机器学习课程笔记，上面好像说过线性回归、逻辑回归、softmax回归可以统一为一种模型，所以决定直接把之前的课程笔记（英文原版的，网上貌似有翻译过的，但是感觉还是看原版更好）再好好研究一下，真正把回归问题搞清楚。另外，这是我第一次写博客，希望以后能够越写越好，有写的不对或者不好的地方，还希望大家能够指点一下。

2.回忆逻辑回归模型

查了一下回归问题的定义，百度百科给出的定义如下：研究一个随机变量Y对另一个(X)或一组(X1，X2，…，Xk)变量的相依关系的统计分析方法。对于一般的回归问题来说，常见的步骤如下：
1. 寻找预测函数(hypothesis) hθ(x)
2. 构造损失函数(cost/loss function) J(θ) （最小化损失函数的过程对应于预测函数参数的过程）
3. 使用优化算法（牛顿法、梯度下降法等）来最小化损失函数，即优化预测函数的参数）
特别地，对于逻辑回归模型（Logistic Regression Model ）,一般用来处理两分类问题，下面分别针对上面的三个步骤进行解释：

2.1 寻找预测函数

在逻辑回归模型中，预测函数 hθ(x) 使用了sigmoid函数（logistic函数），具体的函数形式如下：

g(z)=11+e−z

sigmoid函数的图像如下，取值范围为(0,1):

下面左图是一个线性的决策边界，右图是非线性的决策边界:

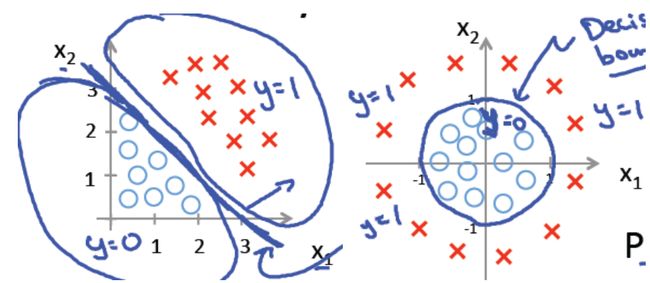
对于线性决策边界的情况，边界函数为：

θ0∗1+θ1∗x1+θ2∗x2+...+θn∗xn=θ⃗ Tx⃗ 

其中 x⃗ =(1,x1,x2,...,xn)T,θ⃗ =(θ0,θ1,...,θn)T ,注意在这里为了表示方便，在 x⃗  中加了常数1项。
根据线性边界函数构造预测函数如下：

hθ⃗ (x⃗ )=1/1+exp(−θ⃗ Tx⃗ )

在这里，预测函数表示目标变量 y 被分类为正样本的概率：

p(y=1|x⃗ ;θ⃗ )=hθ⃗ (x⃗ )

p(y=0|x⃗ ;θ⃗ )=1−hθ⃗ (x⃗ )

至于为什么会选择sigmoid函数，在下面讲GLM的时候会给出具体的推导，具有一定的统计意义。

2.2 构造损失函数

对于逻辑回归，损失函数如下：

J(θ⃗ )=−1m∑imyiloghθ⃗ (xi→)+(1−yi)log(1−hθ⃗ (xi→)）

分析 J(θ⃗ ) 的表达式，可以看出，当 yi 为1时， hθ⃗ (x⃗ ) 越大，即 yi 被预测为1的概率越大，此时损失函数 J(θ⃗ ) 越小； 相反当 yi 为0时， hθ⃗ (x⃗ ) 越小，即 yi 被预测为0的概率越大，此时损失函数 J(θ⃗ ) 越小。
当给定一系列训练样本 (xi,yi)i∈{1,2...m} 时，优化预测函数 hθ⃗ (x) 的过程也就是找到合适的 θ⃗  使得损失函数 J(θ⃗ ) 达到最小值的过程。

至于损失函数 J(θ⃗ ) 具体为什么是上面的形式，同样也会在讲GLM时给出推导过程

2.3 使用优化算法最小化损失函数

在这里，我们只会介绍使用梯度下降法来最小化损失函数，当然还有很多其他的方法可以使用（如牛顿法）：
在梯度下降法中，每次迭代过程中，参数 θ⃗  的更新策略如下：

θi→:=θi−1→−α∂J(θ⃗ )∂θ⃗ |θ⃗ =θi−1→

其中 α 为学习率
下面针对逻辑回归算法给出的推导如下：

因此 θ 的更新公式如下：

θi→:=θi−1→+α1m∑1m(yi−hθ⃗ (xi→))xi→

每次跌代都需要遍历所有样本 (xi,yi) ,因此这种方法也叫 Batch Gradient Descent(批量梯度下降)。还有一种叫Stochastic Gradient Descent(随机梯度下降)，每次迭代只使用一个样本，计算成本更小，一般来说，随机梯度下降法比批量梯度下降法收敛更快，当样本数据集比较大时，经常会选择随机梯度下降法。但是随机梯度下降法可能会造成参数 θ⃗  在最优解周围出现震荡（与样本不能完全线性可分有关），当然也有相应的方法来解决这个问题（迭代过程中动态改变学习率 α ，如需详细了解，可以自己去查一下，在《机器学习实践》这本书也有讲到）。

3. 广义线性模型（GLM）的引入

广义线性模型是基于指数分布族的，而指数分布族的原型如下

p(y;η)=b(y)exp(ηTT(y)−a(η))

其中 η 为 自然参数（natural/canonical parameter）， T(y) 为 充分统计量，也可以是一个向量（softmax regression中就是），通常来说 T(y)=y , exp(−a(η)) 为归一化项，保证 p(y;η) 累加和为1.
不同的 T,a,b 定义了一个以 η 为参数的分布簇(family)，不同的 η 对应了这个簇中不同的分布。值得注意的是，可以证明伯努利分布（跟logistic regression、softmax regression有关）、高斯分布(跟linear regression有关)、泊松分布（当然是跟poission regression有关）都是指数分布簇，后面将给出一些证明.

那么如何根据指数分布簇构造广义线性模型呢？广义线性模型基于下面三个假设：
1. 给定特征属性 x 和参数θ后， y 的条件概率p(y|x;θ)服从指数分布族，即 y|x;θ∼ExpFamily(η)
2. 给定特征属性 x ，我们的目标是预测T(y)的期望值，即 E[T(y)|x] (通常情况下， T(y)=y ,因此 hθ(x)=E[y|x] , 如在逻辑回归模型中， hθ(x)=0∗p(y=0|x)+1∗p(y=1|x)=E[y|x] )
3. η 与 x 之间的关系是线性的，即η=θ⃗ Tx⃗ 

下面将证明线性回归、逻辑回归、softmax回归（逻辑回归是其两分类其情况）其实都属于广义线性模型的范畴：

3.1 线性回归

关于高斯分布的知识在这就不多说了，如果把它看着指数分布簇，那么：

p(y)=12π−−√σexp(−(y−u)22σ2)=(12π−−√σexp(−y22σ2))∗exp(uσ2y−u22σ2)b(y)=12π−−√σexp(−y22σ2),η=uσ2,a(η)=−u22σ2

为了方便证明，在这里我们假设 σ2=1
按照GLM的假设2， hθ(x)=E[y|x]=u=η ，按照假设3， η=θ⃗ Tx⃗  ,因此 hθ(x)=θ⃗ Tx⃗  。此时：

p(y|x;θ⃗ )=12π−−√exp(−(y−θ⃗ Tx⃗ )22)

假设所有的样本相互之间是独立的，则有
p(y|X⃗ ;θ⃗ )=∏mi=1p(yi|xi;θ⃗ )=∏mi=112π√exp(−(yi−θ⃗ Txi→)22)
给定样本集，令 L(θ)=L(θ;X⃗ ,y)=p(y|X⃗ ;θ⃗ ) , L(θ) 即为似然函数，按照最大似然准则，即需要找到 θ⃗  使得 L(θ) 达到最大，但是我们不直接最大化 L(θ) ,为了方便计算，我们对 L(θ) 取对数（对数似然函数 l(θ) (log likelihood)）:

l(θ)=log(L(θ))=const−12∑i=1m(yi−θ⃗ Txi→)2

最大化 L(θ) 等价于最小化 J(θ) ：

J(θ)=12∑i=1m(yi−θ⃗ Txi→)2

这也就是我们在线性回归里面使用LMS准则的损失函数。

如上所示，线性回归实际上就是指数函数簇为高斯分布时的广义线性模型。

3.2 逻辑回归

与线性回归一样，逻辑回归实际上是对应于指数函数簇为伯努利分布(Bernoulli Distribution)时的广义线性模型。下面给出证明：
对于二元的伯努利分布Bernoulli( ϕ )， p(y=1)=ϕ,p(y=0)=1−ϕ ,可以综合表示为以下形式：

p(y)=ϕy(1−ϕ)1−y

现在将伯努利分布表示为指数簇函数形式：

p(y)=exp(log(p(y))=exp(ylog(ϕ)+(1−y)log(1−ϕ))=exp(log(ϕ1−ϕ)y+log(1−ϕ))b(y)=1,η=log(ϕ1−ϕ),a(η)=log(1−ϕ)

根据GLM的假设2， hθ(x)=E[y|x;θ]=ϕ=11+e−η ,按照假设3， η=θ⃗ Tx⃗  ,因此 hθ(x)=11+e−θ⃗ Tx⃗  ,其中 ϕ=11+e−η 就是我们说的sigmoid函数，这也是为什么逻辑回归的预测函数选了sigmoid函数。
与线性回归一下，假设样本之间相互独立，则似然函数 L(θ⃗ ) 为：

L(θ⃗ )=∏i=1mp(yi|xi;θ⃗ )=∏i=1mhθ(xi)yi(1−hθ(xi))1−yi

同样对似然函数取对数：

l(θ)=log(L(θ))=∑i=1myiloghθ(xi)+(1−yi)log(1−hθ(xi))

最大化 L(θ) 也就相当与最小化

J(θ⃗ )=−1m∑imyiloghθ⃗ (xi→)+(1−yi)log(1−hθ⃗ (xi→))

这也就从统计意义上解释了逻辑回归中损失函数的由来。

3.3 softmax回归

现在让我们来考虑一下k分类问题，即与逻辑回归不同，逻辑回归中y取值只能为0或1，对于k分类问题，y的取值为 {1,2,...,k} , 假设y取值为 {1,2,...,k} 的概率分别为 {ϕ1,ϕ2,...,ϕk} ,即 p(y=i)=ϕi 当然这k个参数必须要满足归一化条件 ∑mi=1ϕi=1 (自由度为k-1),与伯努利分布一样，我们可以将y的分布写成一下格式：

y=ϕ1{y=1}1ϕ1{y=2}2...ϕ{y=k}k

其中 1{∗} 为示性函数，1{True} = 1,1{False}=0
我们定义 T(y)∈Rk−1 如下：

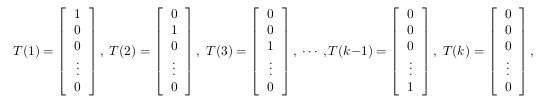
其中 (T(y))i=1{y=i} ,利用T(y)重新表示y的分布：

y=ϕT(y)11ϕT(y)22...ϕ1−∑mi=1T(y)ik=exp(T(y)1log(ϕ1)+T(y)2log(ϕ2)+...+T(k−1)log(ϕk−1)+(1−∑i=1mT(y)i)log(ϕk))=exp(log(ϕk)+∑i=1k−1T(y)ilog(ϕiϕk))=exp(log(ϕk)+ηTT(y))

其中 η=(η1,η2,...,ηk−1)=(logϕ1ϕk,logϕ2ϕk,...,logϕk−1ϕk)T,b(y)=1,a(η)=log(ϕk)
由假设2可知， hθ(x)=E[T(y)|x]=(ϕ1,ϕ2,...,ϕk−1)T ,由假设3可知：

log(ϕiϕk)=ηi=θi→Tx⃗ ϕi=exp(θi→Tx⃗ )ϕk

再由归一化条件可知， ∑ki=1ϕi=1 ,则可计算得到：

p(y=i|x)=ϕi=eθi→Tx⃗ 1+∑k−1j=1eθj→Tx⃗ 

为了表示方便，我们可以定义 ηk=log(ϕkϕk)=0 ，即 θk→=0⃗  ,则上式可以重新表示为：

p(y=i|x)=ϕi=eθi→Tx⃗ ∑kj=1eθj→Tx⃗ 

这也就是我们所熟知的softmax回归模型，预测的目标函数为：

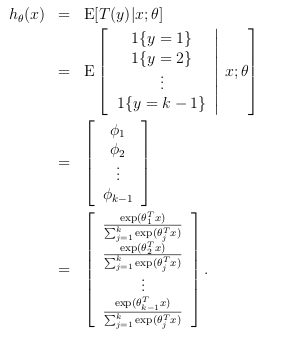
当k=2时，softmax回归便退化为前面的逻辑回归模型。

至此，我们已经完成了对线性回归模型、逻辑回归模型、softmax模型的推导，其实把分布簇函数换成泊松分布，你就可以推导出泊松回归了。

结束语

公式实在太多，搞了差不多一天，终于完成了自己的第一篇博客，希望能够对希望了解回归的同学有点帮助，时间匆忙，文中可能会有些错误，还希望大家能够多多包涵，多多指点，欢迎交流。《机器学习实践》这本书中有具体的实现代码，大家有时间最好还是动手实践一下，能够加深理解！

http://blog.csdn.net/dongtingzhizi/article/details/15962797
http://blog.csdn.net/lilyth_lilyth/article/details/10032993
http://blog.csdn.net/acdreamers/article/details/44663091
Andew Ng 机器学习lecture notes
《机器学习实践》