数据结构概述（逻辑结构与存储结构概念详解）

目录

一.一些基本概念

二.逻辑结构

1.集合结构：

2.线性结构：

1）线性表：

2）栈

3）队列

4）串

3.非线性结构：

1）数组

2）广义表

3）树

4）堆

5）图

三.物理结构/存储结构

1.顺序结构：

2.链式结构：

3.索引结构：

---

数据结构就是研究数据的逻辑结构和物理结构以及它们之间的相互关系，并对这种结构定义相应的运算，且确保经过这些运算后所得到的新结构仍然是原来的结构类型。简单来说，就是计算机存储、组织数据的方式。

一.一些基本概念

程序=数据结构+算法；同一逻辑结构可以对应不同的存储结构，算法的设计取决于数据的逻辑结构，算法的实现依赖于指定的存储结构。

数据：所有能被输入到计算机中，且能被计算机处理的符号的集合。是计算机操作的对象的总称；
数据元素：数据（集合）中的一个“个体”，数据及结构中讨论的基本单位；
数据项：数据的不可分割的最小单位。一个数据元素可由若干个数据项组成；
数据类型：在一种程序设计语言中，变量所具有的数据种类。整型、浮点型、字符型等等。

二.逻辑结构

反映数据元素之间的逻辑关系。

1.集合结构：

数据元素除了同属一个集合外，它们之间没有任何关系。

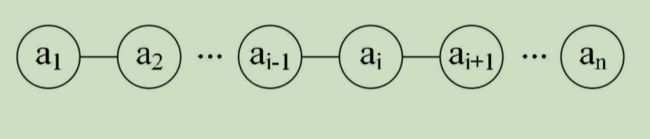
2.线性结构：

若结构是非空集，则有且仅有一个开始结点和一个终端结点，并且所有结点都最多只有一个直接前趋和一个直接后继。简单地说，就是数据之间是一对一的关系。有线性表、栈、堆、队列、串等。

1）线性表：

是n个具有相同特性的数据元素的有限序列；

数据元素之间一对一的关系，除了首尾数据元素外，其它数据元素都是首位相接的；

线性指逻辑层次上的线性，不考虑存储层次，双向链表和循环链表也是线性表；

单向链表：除了首尾数据元素外，其它数据元素都是首位相接的。

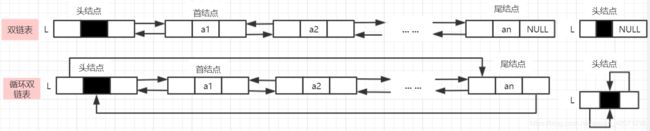
双向链表：由节点组成，每个数据结点中都有两个指针，分别指向直接后继和直接前驱。

循环单链表：把单链表改为循环单链表的过程是将它的尾结点next指针域由原来为空改为指向头结点，整个单链表形成一个环。由此，从表中任一结点出发均可找到链表中的其他结点。

循环双链表：把双链表改为循环双链表的过程是将它的尾结点next指针域由原来为空改为指向头结点，将它的头结点prior指针域改为指向尾结点，整个双链表形成两个环。

线性表-双链表&循环链表(Ⅳ)_—Miss. Z—的博客-CSDN博客

2）栈

栈只能从表的一端存取数据，另一端是封闭的；

在栈中存/取数据，必须遵循“先进后出”原则，即最先进栈的元素最后出栈；

开口端称为栈顶，距离栈顶最近的元素称为栈顶元素，封口端称为栈底，相应的有栈底元素；

向栈中添加元素称为“进栈/入栈/压栈”，从栈中提取指定元素称为“出栈/弹栈”；

有顺序栈和链栈两种实现方式，区别仅限于数据元素在实际物理空间上存放的相对位置，顺序栈底层采用的是数组，链栈底层采用的是链表。

顺序栈及基本操作（包含入栈和出栈）

链栈及基本操作（包含入栈和出栈）详解

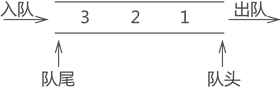
3）队列

进数据的一端为“队尾”，出数据的一端为“队头”，进队过程称为“入队”，出队过程称为“出队”；

遵循“先进先出”原则；

队列存储结构的实现也由顺序队列和链队列两种方式，详细可参考文章：

顺序队列及C语言实现（2种方案）

链式队列及基本操作（C语言实现）

4）串

指字符串，数据元素仅由一个字符组成，字符串本身是由零个或多个字符组成的有限序列；

S1=“SHANG”，S1是串名，双引号括起来的字符序列为串值，引号本身不属于串的内容；

详细可参考文章：

数据结构：串(String)【详解】_UniqueUnit的博客-CSDN博客_串 数据结构

3.非线性结构：

一个结点可能有多个直接前趋和直接后继。有数组、广义表、树（一对多）、堆、图（多对多）等。

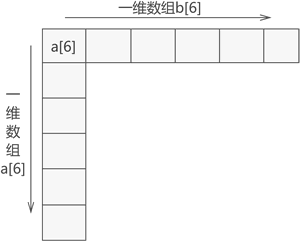
1）数组

        顺序表、链表、栈和队列存储的都是不可再分的数据元素（如数字 5、字符 'a' 等），而数组既可以用来存储不可再分的数据元素，也可以用来存储像顺序表、链表这样的数据结构。数组可以直接存储多个顺序表。

二维数组理解为存储一维数组的一维数组：（图为二维数组存储结构示意）

n维数组理解为存储n-1维数组的一维数组。

2）广义表

数组可以存储不可再分的数据元素，也可以继续存储数组，但是两种数据存储形式不会出现在同一数组中。例如，我们可以创建一个整形数组去存储 {1,2,3}，我们也可以创建一个二维整形数组去存储 {{1,2,3},{4,5,6}}，但数组不适合用来存储类似 {1,{1,2,3}} 这样的数据。此时更适合用广义表。

记作：LS = (a1,a2,…,an)，广义表中每个 ai 既可以代表单个元素，也可以代表另一个广义表。；

存储的单个元素称为 "原子"，而存储的广义表称为 "子表"；

不是空表时，称第一个数据（原子或子表）为"表头"，剩下的数据构成的新广义表为"表尾"；

3）树

存储的是具有“一对多”关系的数据元素的集合。

使用树结构存储的每一个数据元素都被称为“结点”；

每一个非空树都有且只有一个被称为根的结点；

如果结点没有任何子结点，那么此结点称为叶子结点（叶结点）；

对于一个结点，拥有的子树数（结点有多少分支）称为结点的度（Degree）；

一棵树的深度（高度）是树中结点所在的最大的层次；

由 m（m >= 0）个互不相交的树组成的集合被称为森林。

4）堆

如果有一个关键码的集合K = {k0，k1， k2，…，kn-1}，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足：Ki <= K2i+1 且 Ki<=K2i+2 ，则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

堆中某个结点的值总是不大于或不小于其父节点的值；

堆总是一棵完全二叉树。

堆的算法实现可参考文章：

数据结构之堆_Hidden.Blueee的博客-CSDN博客_堆

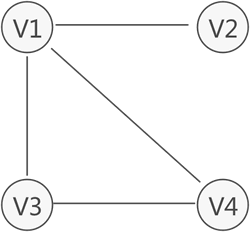
5）图

有向图：

图中存储的各个数据元素被称为顶点（而不是节点）；

可细分两种表现类型，分别为无向图和有向图；

有向图中，无箭头一端的顶点通常被称为"初始点"或"弧尾"，箭头直线的顶点被称为"终端点"或"弧头"；

对于有向图中的一个顶点 V 来说，箭头指向 V 的弧的数量为 V 的入度；箭头远离 V 的弧的数量为 V 的出度；

详细可参考文章：

数据结构图，图存储结构详解

三.物理结构/存储结构

1.顺序结构：

数据元素存放在地址连续的存储单元里，数据间的逻辑关系和物理关系一致，不方便插入和删除。内存空间是连续的。

2.链式结构：

数据元素存放在任意的存储单元里，这组存储单元可以连续也可以不连续，需要一个指针存放数据元素的地址。

链表中的第一个结点的存储位置称为头指针，第一个结点称为头结点，头结点分为虚拟头结点和真实头结点；

存储数据元素信息的域称为数据域，把存储直接后继位置的域称为指针域；

指针域中存储的信息称为指针或链，数据域和指针域两部分信息组成的数据元素称为存储映像（结点）；

n个结点链接成一个链表，即为线性表的链式存储结构；

链表中的每个结点中只包含一个指针域则称为单链表。

一些基本概念介绍：

一个结点如下：

单链表的结构如下：’

 虚拟头结点：指第一个结点不存储数据，只用来指向下一个结点的地址，如下图红色结点：

真实头结点：第一个结点用来存储数据

 

 数据结点：链表中代表数据元素的结点；

尾结点：链表中最后一个数据结点，包含的地址信息为空。

代码实现相关细节可参考文章：

链式存储结构_yiquanlaoshi的博客-CSDN博客_链式存储结构

3.索引结构：

例如，B Tree（B树）/多路平衡搜索树：

• 叶节点具有相同的深度，叶节点的指针为空

• 所有索引元素不重复

• 节点中的数据索引从左到右递增排列

索引详细介绍可参考文章：

索引及其实现结构_月亮在我手上 ³的博客-CSDN博客