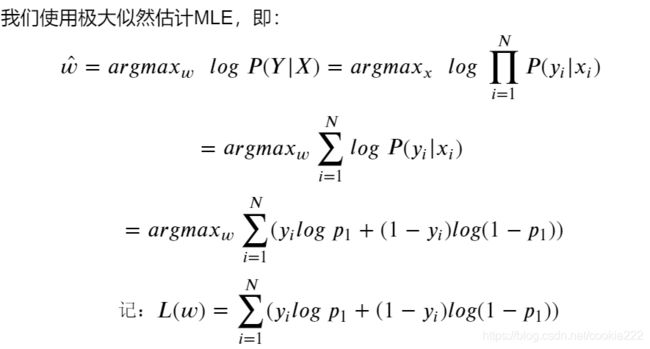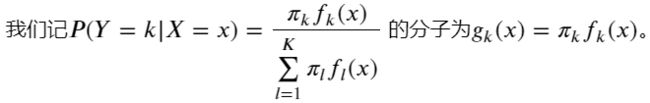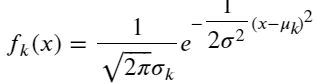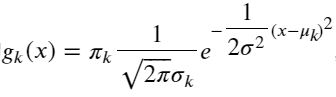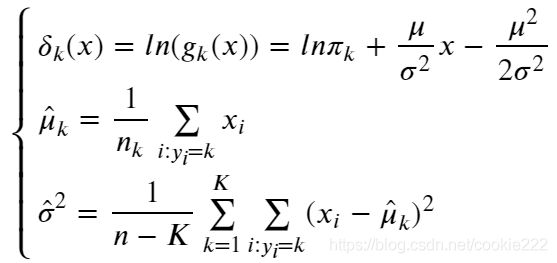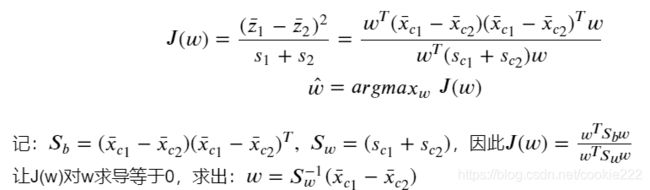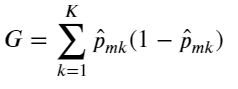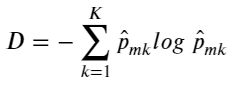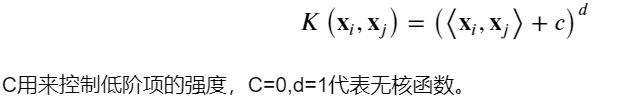集成学习04-分类问题

 使用sklearn构建完整的分类项目：
（1）收集数据集并选择合适的特征
（2）选择度量模型性能的指标
（3）选择具体的模型并进行训练
（4）评估模型的性能并调参

---

度量模型性能的指标

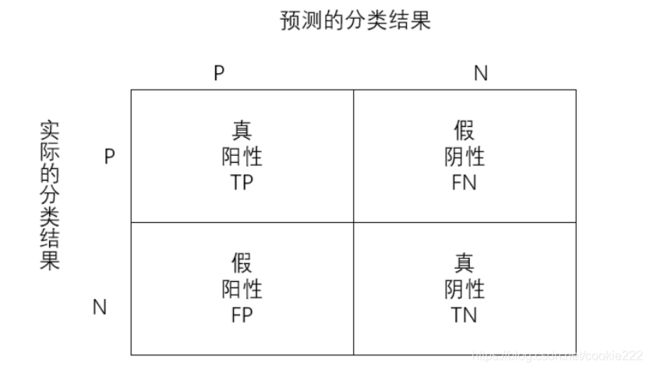
4种情况：

• 真阳性TP：预测值和真实值都为正例；
• 真阴性TN：预测值与真实值都为正例；
• 假阳性FP：预测值为正，实际值为负；
• 假阴性FN：预测值为负，实际值为正；

• 分类模型的指标：
• 准确率：分类正确的样本数占总样本的比例，即：
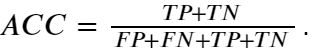
• 精度：预测为正且分类正确的样本占预测值为正的比例，即：
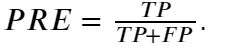
• 召回率：预测为正且分类正确的样本占类别为正的比例，即：
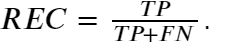
• F1值：综合衡量精度和召回率，即：
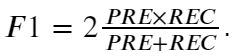
• ROC曲线：以假阳率为横轴，真阳率为纵轴画出来的曲线，曲线下方与坐标轴的面积越大越好。

 

---

常见的分类模型如下：

1. 逻辑回归

假设线性回归模型为 =0+1，使用logistic函数将线性回归的结果转化为概率，y取0或1。

logistic函数： 

2. 线性判别分类

（1）贝叶斯公式角度：

 在这里， 我们做个模型假设：假设()服从正态分布，

 

（2）降维的角度：

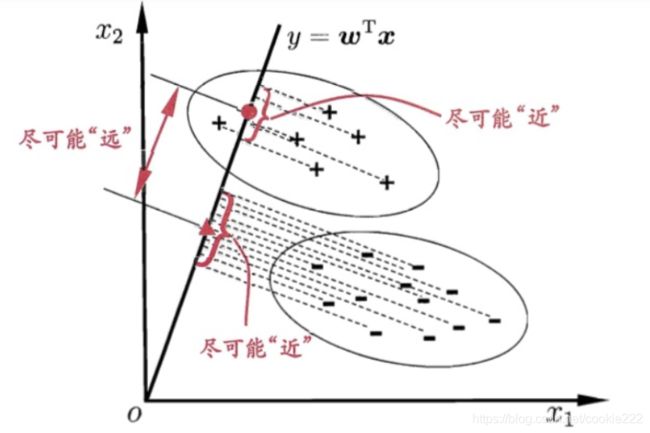
基于数据进行分类时，一个很自然的想法是：将高维的数据降维至一维，然后使用某个阈值将各个类别分开。下面用图的形式展示：

思想：降维后的样本投影点，类内方差小，类间方差大。

类间方差用不同类的投影中心(类的均值)的距离来表示。

（3）朴素贝叶斯：对线性回归分类的简化

在线性判别分析中，我们假设每种分类类别下的特征遵循同一个协方差矩阵，每两个特征之间是存在协方差的，因此在线性判别分析中各种特征是不是独立的。但是，朴素贝叶斯算法对线性判别分析作进一步的模型简化，它将线性判别分析中的协方差矩阵中的协方差全部变成0，只保留各自特征的方差，也就是朴素贝叶斯假设各个特征之间是不相关的。在之前所看到的偏差-方差理论中，我们知道模型的简化可以带来方差的减少但是增加偏差，因此朴素贝叶斯也不例外，它比线性判别分析模型的方差小，偏差大。

判别模型vs生成模型：

判别模型只需计算出数值，比较得出输出概率最大的类别。

生成模型必须计算出p(y|x)的分布，分母在高维空间中很难求出积分，计算常采用MCMC采样。

3. 决策树分类

与决策树回归大致是一样的，只是在回归问题中，选择分割点的标准是均方误差，但是在分类问题中，由于因变量是类别变量而不是连续变量，因此用均方误差显然不合适。那问题是用什么作为选择分割点的标准呢？

分类树与回归树区别：分裂节点的指标不同，预测的值不同。回归树预测的是区域内的均值，分类树预测的是区域内最常出现的类（预测均值无法代表类别）。

在回归树中，对一个给定的观测值，因变量的预测值取它所属的终端结点内训练集的平均因变量。与之相对应，对于分类树来说，给定一个观测值，因变量的预测值为它所属的终端结点内训练集的最常出现的类。分类树的构造过程与回归树也很类似，与回归树一样，分类树也是采用递归二叉分裂。但是在分类树中，均方误差无法作为确定分裂节点的准则，一个很自然的替代指标是分类错误率。分类错误率就是：此区域内的训练集中非常见类所占的类别，即：

，̂代表第m个区域的训练集中第k类所占的比例。

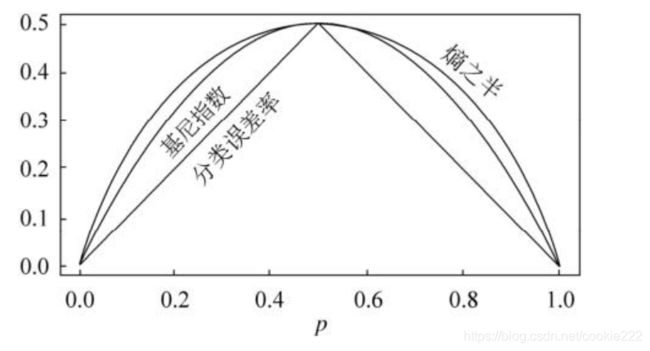
由于分类错误率在构建决策树时不够敏感，一般在实际中用如下两个指标代替：
(1) 基尼系数：

(2) 交叉熵：

 

4. 支持向量机（线性）

想法：找到最大间隔超平面。

 

SVM与神经网络区别：SVM决策平面光滑，神经网络通过多个平面多次划分，不光滑；SVM提高维数来划分类别，神经网络提高层数和神经元数量来划分。

5. 非线性支持向量机（使用核函数）

SVM如何处理非线性问题呢？答案就是将数据投影至更加高的维度！在一维数据做不到线性可分，我们将数据投影至二维平面就可以成功线性可分。

和线性可分SVM的优化目标函数的区别仅仅是将内积.替换为().()。我们要将其映射到超级高的维度来计算特征的内积。这时候映射成的高维维度是爆炸性增长的，这个计算量实在是太大了，而且如果遇到无穷维的情况，就根本无从计算了。

下面引入核函数：
假设是一个从低维的输入空间（欧式空间的子集或者离散集合）到高维的希尔伯特空间的H映射。那么如果存在函数(,)，对于任意,∈，都有核函数：

核函数(,)的计算是在低维特征空间来计算的，它令我们享受在高维特征空间线性可分的好处，却避免了高维特征空间恐怖的内积计算量。下面介绍几种常用的核函数：

(1) 多项式核函数：
多项式核函数（Polynomial Kernel）是线性不可分SVM常用的核函数之一，表达式为：

 (2) 高斯核函数：
高斯核函数（Gaussian Kernel），在SVM中也称为径向基核函数（Radial Basis Function,RBF），它是非线性分类SVM最主流的核函数。表达式为：

 

 (3) Sigmoid核函数：

 (4) 余弦相似度核：
常用于衡量两段文字的余弦相似度，表达式为：

 

---

作业：

1.回归问题和分类问题的联系和区别，如何利用回归问题理解分类问题？
联系：都是通过训练样本预测未知的值。

区别：分类问题中，输出为类别(离散值)；而在回归问题中，输出可取任意实数(连续值)。

逻辑回归中，与线性回归的思想相同，用一个线性函数拟合各个样本。区别只是使用sigmoid函数，将预测值y从实数轴上的数转换为[0,1]区间上的概率p，用概率确定样本属于哪个类别。

2.为什么分类问题的损失函数可以是交叉熵而不均方误差？
1）在逻辑回归中，使用最大似然估计(|)，最大化事件发生概率<==>最小化交叉熵，因此可以把交叉熵看作损失函数。2）分类问题的预测值是类别，类别与定义的数值没有太大关系，预测值的均值无法衡量模型的误差。 

3.线性判别分析和逻辑回归在估计参数方面有什么异同点？

4.尝试从0推导svm.（拓展题，也是面试题）

5.二次判别分析，线性判别分析，朴素贝叶斯之间的联系和区别？
判别分析包括可用于分类和降维的方法。线性判别分析（LDA）特别受欢迎，因为它既是分类器又是降维技术。二次判别分析（QDA）是LDA的变体，允许数据的非线性分离。最后，正则化判别分析（RDA）是LDA和QDA之间的折衷。

6.使用python+numpy实现逻辑回归。（必做题）

from sklearn import datasets, metrics
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

def sigmoid(z):
    return 1 / (1 + np.exp(-z))
def grad_descent(dataMatIn, classLabels):
    dataMatrix = np.mat(dataMatIn)  #(m,n)
    labelMat = np.mat(classLabels).transpose()
    m, n = np.shape(dataMatrix)
    weights = np.ones((n, 1))  #初始化回归系数（n, 1)
    alpha = 0.001 #步长
    maxCycle = 500  #最大循环次数
    # 调整权重
    for i in range(maxCycle):
        h = sigmoid(dataMatrix * weights)  #sigmoid 函数
        weights = weights + alpha * dataMatrix.transpose() * (labelMat - h)  #梯度
    return weights, h

iris = datasets.load_iris()
X = iris.data
y = iris.target
X = np.insert(X, 0, 1, axis=1)  # 特征数据集，添加1是构造常数项x0
w = grad_descent(X, y)
print("权重w为：", w)

7.了解梯度下降法，牛顿法，拟牛顿法与smo算法等优化算法。（拓展题）

最优化/Optimization文章合集https://www.codelast.com/%e5%8e%9f%e5%88%9b%e6%9c%80%e4%bc%98%e5%8c%96optimization%e6%96%87%e7%ab%a0%e5%90%88%e9%9b%86/#more-7364