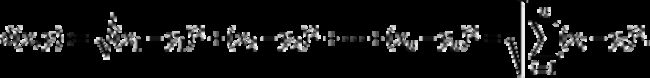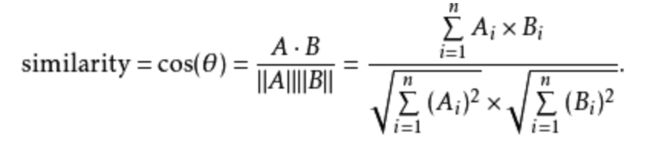机器学习-各类距离的定义
两个向量之间的距离(此时向量作为n维坐标系中的点)计算,在数学上称为向量的距离(distance),也称为样本之间的相似性度量(Similarity Measurement)
它反映为某类事物在距离上接近或远离的程度。直觉上,距离越近的就越相似,越容易归为一类;距离越远就越不同。
范数
向量的范数可以简单、形象地理解为向量的长度,或者向量到坐标系原点的距离,或者相应空间内的两点之间的距离。
1.闵可夫斯基距离(Minkowski Distance)
严格意义上讲,闵可夫斯基距离不是一种距离,而是一组距离的定义。
两个n维变量A(x1,x2,....xn)与B(y1,y2,...yn)间的闵可夫斯基距离定义为
其中p是一个变参数
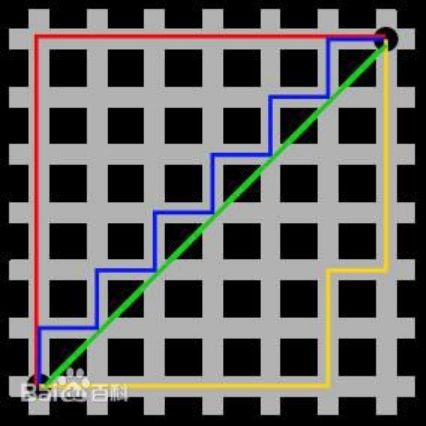
- 当p=1时,就是曼哈顿距离(两个点在标准坐标系上的绝对轴距之和)
下方图片中的红线
蓝色、黄色为等价的曼哈顿距离
- 当p=2时,就是欧式距离(勾股定理计算两个点的直线距离)
下方图片中的绿线
二维空间距离公式
三维空间距离公式
n维空间距离公式
- 当p->∞ 时,就是切比雪夫距离
2.欧氏距离(Euclidean Distance)
勾股定理求,点之间的直线距离
二维空间距离公式
三维空间距离公式
n维空间距离公式
3.曼哈顿距离(Manhattan Distance)
两个点在标准坐标系上的绝对轴距之和
二维平面两点A(x1,y1),B(x2,y2)间的曼哈顿距离
d12=|x1-x2|+|y1-y2|
两个n维向量A(x11,x12....,x1n)与B(x21,x22,....,x2n)间的曼哈顿距离
d12=累加|x1k-x2k|(k从1到n)
4.切比雪夫距离(Chebyshev Distance)
二维平面两点A(x1,y1),B(x2,y2)间的切比雪夫距离
d12=max(|x1-x2|,|y1-y2|)
两个n维向量A(x11,x12....,x1n)与B(x21,x22,....,x2n)间的切比雪夫距离
d12=max(|x1i-x2i|)
5.夹角余弦(Cosine)
夹角余弦可以用来衡量两个向量方向的差异,机器学习中借用这一概念来衡量样本向量之间的差异
可以使用类似于夹角余弦的概念来衡量它们间的相似度
夹角余弦取值范围为[-1,1]。夹角余弦越大,表示两个向量的夹角越小;夹角余弦越小,表示两个向量的夹角越大。
当两个向量的方向重合时,夹角余弦取最大值1;当两个向量的方向完全相反时,夹角余弦取最小值-1.
夹角余弦值与夹角成反比。
6.汉明距离(Hamming Distance)
两个等长字符串s1与s2之间的汉明距离定义为将其中一个变为另外一个所需要的最小替换次数。
如:字符串’1111’与‘1001’之间的汉明距离为2.
7.杰卡德相似系数(Jaccard Similarity Coefficient)
- 杰卡德相似系数:
两个集合A和B的交集元素在A、B的并集中所占的比例,称为两个集合的杰卡德相似系数。用符号J(A,B)表示
J(A,B) = |A∩B| / |A∪B|
杰卡德相似系数是衡量两个集合的相似度的一种指标。
- 杰拉德距离:
杰卡德距离用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度。
杰卡德距离 = 1 - J(A,B) = (|A∪B| - |A∩B|) / |A∪B|
杰卡德相似系数与杰卡德距离的应用
可将杰卡德相似系数用在衡量样本的相似度上
样本A与样本B是两个n维向量,而且所有维度的取值都是0或1.例如A(0111)和B(1011)。我们将样本看成一个集合,1表示集合包含该元素,0表示集合不包含该元素。
p:样本A与B都是1的维度的个数
q:样本A是1、样本B是0的维度的个数
r:样本A是0、样本B是1的维度的个数
s:样本A与B都是0的维度的个数
样本A与B的杰卡德相似系数可以表示为
J(A,B) = p / (p + q + r)
这里p+q+r可理解为A与B的并集的元素个数,而p是A与B的交集的元素个数。
附:相关计算Python代码
from numpy import *
import numpy as np
import scipy.spatial.distance as dist
#欧式距离(勾股定理)
def euclidean(vector1, vector2):
result = sqrt((vector1 - vector2) * ((vector1 - vector2) .T))
return result
#曼哈顿距离(两点在标准坐标系中的绝对轴距之和)
def manhattan(vector1, vector2):
result = sum(abs(vector2 - vector1))
return result
#切比雪夫距离(点之间的最大距离)
def chebyshev(vector1, vector2):
result = abs(vector2 - vector1).max()
return result
#夹角余弦(取值范围[-1,1].当两个向量的方向重合时,夹角余弦取最大值1,当两个向量方向完全相反时,取最小值-1)
def cosine(vector1, vector2):
v1 = np.squeeze(np.asarray(vector1))
v2 = np.squeeze(np.asarray(vector2))
result = dot(v1, v2) / (linalg.norm(vector1) * linalg.norm(vector2))
return result
#汉明距离(一个字符串变为另一个字符串所需要的最小替换次数)
def hamming(vector1, vector2):
smstr = nonzero(vector1 - vector2)
result = shape(smstr[0])[0]
return result
#杰卡德相似系数(两集合交集占并集的比例)
def jaccard(matV):
result = dist.pdist(matV, 'jaccard')
return result
vector1 = mat([1, 2, 3])
vector2 = mat([4, 5, 6])
matV = mat([[1, 1, 0, 1, 0, 1, 0, 0, 1], [0, 1, 1, 0, 0, 0, 1, 1, 1]])
print('欧氏距离:', euclidean(vector1, vector2))
print('曼哈顿距离:', manhattan(vector1, vector2))
print('切比雪夫距离:', chebyshev(vector1, vector2))
print('夹角余弦:', cosine(vector1, vector2))
print('汉明距离:', hamming(matV[0], matV[1]))
print('杰卡德相似系数:', jaccard(matV))