全15万字丨PyTorch 深度学习实践、基础知识体系全集;忘记时,请时常回顾。
✨ ✨我们抬头便看到星光,星星却穿越了万年. ✨ ✨
作者主页:追光者♂
个人简介:在读计算机专业硕士研究生、CSDN-人工智能领域新星创作者、2022年度博客之星人工智能领域TOP4、阿里云开发者社区专家博主 2023励志在10月底成为CSDN Blog Experts 【无限进步,一起追光!】
欢迎点赞 收藏⭐ 留言
本篇是关于深度学习框架——PyTorch 的基础练习,面向 初学者/复习者/遗忘者。一定要多次回顾!!!请相信:这是神经网络/深度学习 触类旁通的基础!
万丈高楼平地起,地基不牢可不行~ 模型简单,但极其重要,请重视哦!
参考视频学习内容,在文末统一指出。
阅读目录
- 一、基础 模型&算法 回顾
-
- 1.1 线性模型
-
- 1.1.1 基础练习 y ^ = ω x \widehat y=\omega x y =ωx
- 1.1.2 练习 y ^ = ω x + b \widehat y=\omega x+b y =ωx+b
- 1.1.3 其它:在深度学习训练中,横轴往往是Epoch
- 1.2 Gradient Descent(梯度下降)
-
- 1.2.1 梯度下降法 的由来:问题背景
- 1.2.2 何为梯度?
- 1.2.3 梯度下降
- 1.2.4 梯度下降的公式 如何得来的?(理解)
- 1.2.5 随机梯度下降(Stochastic gradient descent,SGD);Mini-batch!
- 1.2.6 梯度下降练习:方法一(推荐 完全 自己 多手写几遍)
- 1.2.7 方法二(与法一类似,不过这里 纵轴 是 权值的 收敛变化 收敛变化 收敛变化)
- 1.2.8 随机梯度下降练习(一),可视化
- 1.2.9 随机梯度下降练习(二),可视化
- 1.3 反向传播(Back Propagation)
-
- 1.3.1 从 神经网络视角下 来看:
- 1.3.2 “计算图” 中的 神经网络;由 单纯添加层数的“无效复杂” 到 添加 非线性激活函数(如sigmoid/ReLU/等)后的“有效复杂”
- 1.3.3 反向传播的过程;前馈计算,反向传播!
- 1.3.4 附:PyTorch中的 前馈与反馈;Tensor!
- 1.3.5 PyTorch反向传播练习(1) y ^ = ω x \widehat y=\omega x y =ωx
- 1.3.6 PyTorch反向传播练习(2) y ^ = ω 1 x 2 + ω 2 x + b \widehat y=\omega_1 x^2 + \omega_2x + b y =ω1x2+ω2x+b
- 1.3.7 补充——针对1.3.5,可视化,看权重收敛情况。 y ^ = ω x \widehat y=\omega x y =ωx
- 1.3.8 补充——针对1.3.6,可视化,看参数w1、w2、b收敛情况 y ^ = ω 1 x 2 + ω 2 x + b \widehat y=\omega_1 x^2 + \omega_2x + b y =ω1x2+ω2x+b
- 1.4 线性回归——使用PyTorch实现 y ^ = ω x + b \widehat y = \omega x +b y =ωx+b
-
- 1.4.1 Pytorch深度学习的一般流程
- 1.4.2 线性单元----Linear Unit
- 1.4.3 练习(训练周期:前馈、反馈、权重更新)
- 1.4.4 练习2——测试一下其它优化器效果如何
- 1.5 逻辑回归 (LogisticRegression)——基于PyTorch实现
-
- 1.5.1 问题背景——二分类问题
- 1.5.2 常做练习用的数据集介绍:MNIST 和 CIFAR-10
- 1.5.3 二分类 与 sigmoid
- 1.5.4 模型的变化:由线性回归模型---->二分类模型,增添sigmoid函数;损失函数的变化:由线性回归损失函数(MSE 均方误差损失函数) ---->二分类损失函数BCELoss (mini-batch 小批量交叉熵损失函数cross entropy)
- 1.5.5 code练习
- 1.6 处理多维特征的输入
-
- 1.6.1 问题背景,含 多维特征 的数据集
- 1.6.2 多维度特征的处理;Mini-batch;多层神经网络
- 1.6.3 练习
- 1.6.4 可视化,使用 Adam优化器/SGD优化器 试试看
- 1.6.5 附:可尝试 不同的激活函数
- 1.7 加载数据集 Dataset and DataLoader
-
- 1.7.1 Dataset类、DataLoader类;Epoch、Mini-batch、Iteration;
- 1.7.2 DataLoader类 核心参数解释
- 1.7.3 如何在代码层面实现 Dataset和DataLoader
- 1.7.4 其它说明:torchvision内置数据集
- 1.7.5 练习(1)【建议取num_workers=0;若=2,速度反而慢了】
- 1.7.6 练习(2),划分训练集、测试集;封装训练过程、测试过程
- 1.7.3 练习(3)使用GPU训练
- 1.8 多分类问题——交叉熵损失函数CrossEntropyLoss:Softmax分类器,One-hot;针对MNIST数据集
-
- 1.8.1 针对多分类问题,输出的概率 应满足“分布”的要求
- 1.8.2 Softmax 计算公式
- 1.8.3 通过softmax得到概率分布后,损失函数Loss如何做?
- 1.8.4 交叉熵损失CrossEntropyLoss = Softmax + 原Loss(即 − Y l o g Y ^ -Y log\widehat Y −YlogY )
- 1.8.5 有了上面的分析,这里如何处理MNIST数据集呢
- 1.8.6 模型
- 1.8.7 练习(1)(未使用GPU)默认CPU
- 1.8.8 练习(2)使用GPU
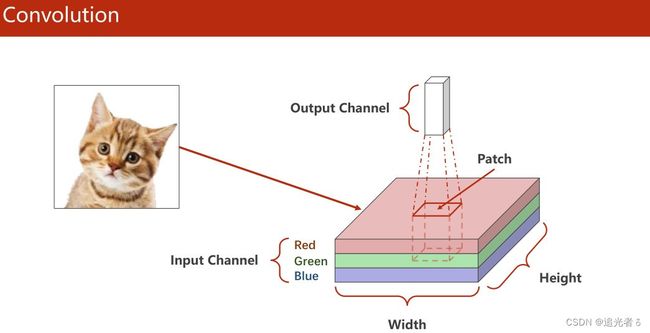
- 1.9 卷积神经网络CNN(基础篇)
-
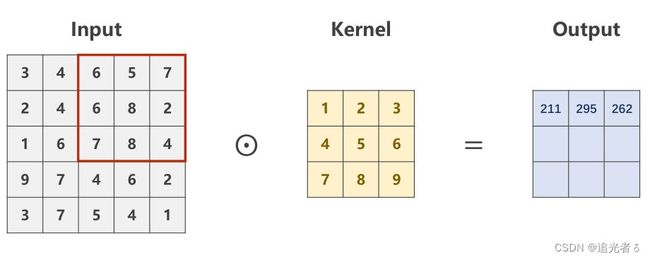
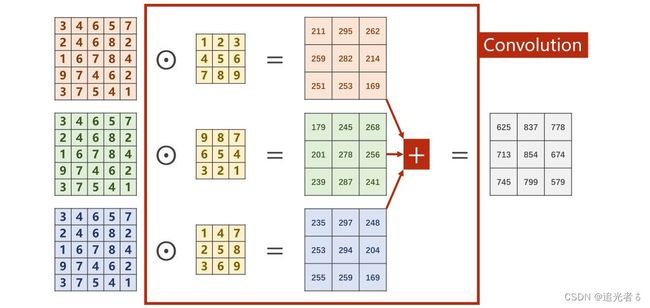
- 1.9.1 基础概念:卷积、卷积运算过程、单通道卷积&多通道卷积、卷积层 权重 w w w的四个维度
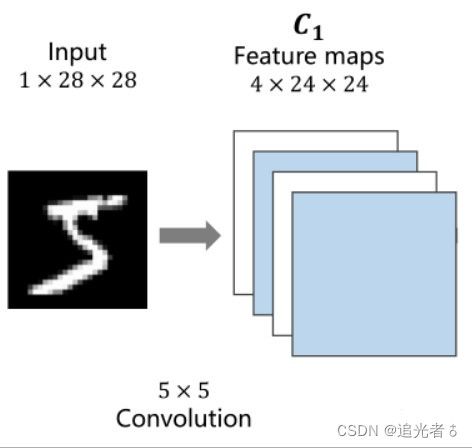
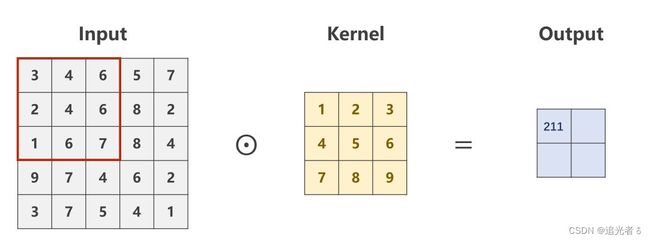
- 1.9.2 CNN计算过程示例
- 1.9.3 改进——padding,一般 外围补0
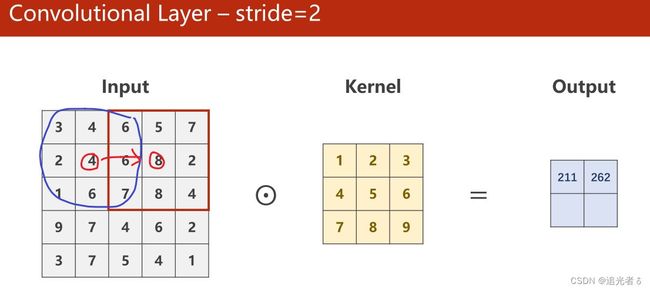
- 1.9.4 改进——步长 stride
- 1.9.5 改进——下采样(又叫“池化”),一般采用 Max Pooling Layer
- 1.9.6 针对MNIST数据集,所采用的模型
- 1.9.7 如何在GPU上来跑(怎么用显卡来计算)
- 1.9.8 练习(1)
- 1.9.9 练习(2)使用GPU来跑
- 1.10 卷积神经网络CNN(高级篇)
-
- 1.10.1 背景,引出更复杂的网络结构(非串行的)
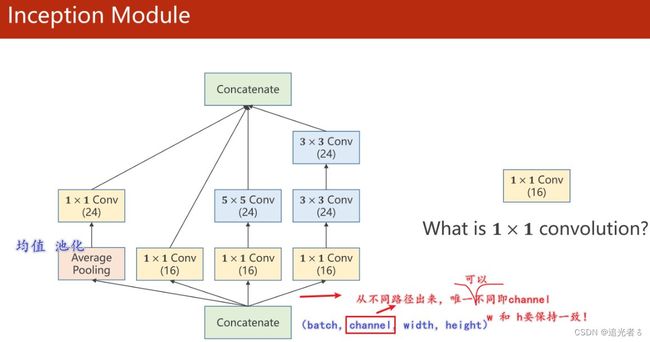
- 1.10.2 非串行网络结构 之 GoogLeNet
- 1.10.3 GoogLeNet:Inception Module,Average Pooling, 1 × 1 1\times1 1×1卷积
- 1.10.4 GoogLeNet 练习
- 1.10.5 GoogLeNet 练习,GPU版
- ----------------------------------分割线----------------------------------
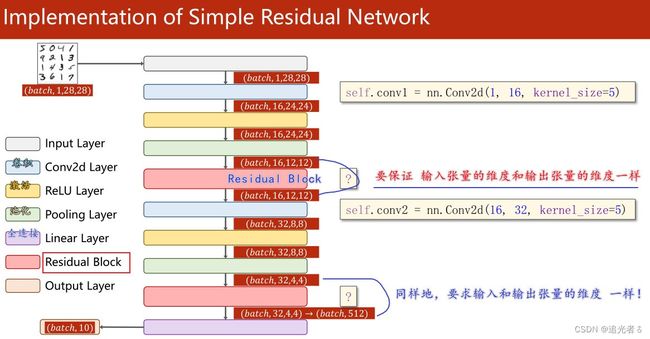
- 1.10.6 ResNet(残差网络)
- 1.10.7 Residual Net:“和 x x x做加法”
- 1.10.8 Residual Net 练习——accuracy=99%
- 1.10.9 Residual Net 练习——GPU版
- 1.10.10 附:其它Residual块 设计——可参阅Paper
- 1.11 循环神经网络RNN(基础篇)
-
- 1.11.1 问题背景,RNN:专门用来处理序列数据
- 1.11.2 RNN的运算
- 1.11.3 构造RNN
- 1.12 循环神经网络RNN(高级篇)
- 二、其他——PyTorch深度学习库的特点
-
- 2.1 Torch简介
- 2.2 PyTorch安装
- 2.3 特点——GPU加速
- 2.4 特点——自动求导
- 2.5 特点——封装的API
- 三、其他——神经网络基础
-
- 3.1 基本原理
- 3.2 正向传播与反向传播
-
- 3.2.1 正向传播
- 3.2.2 反向传播
- 四、传统机器学习策略
- 五、学习系统的发展
-
- 5.1 基于规则的系统
- 5.2 经典机器学习方法
- 5.3 表示学习方法
-
- 5.3.1 维度诅咒
- 5.3.2 解决方法
- 六、人工智能补充知识
-
- 6.1 需要会的必备知识
- 6.2 人工智能——问题分类
-
- 6.2.1 推理
- 6.2.2 预测
- 6.3 人工智能——算法分类
-
- 6.3.1 传统算法与智能算法
- 七、Reference
一、基础 模型&算法 回顾
1.1 线性模型
对于一个算法(模型)。在深度学习中,简要的处理方式是:
准备数据集(Datasets)—>> Model(选择模型) —>> Training (模型训练) —>> 推理(进行推理预测)。
至于优化等,可以理解为后续的补充。
监督学习:数据集需要 交付给算法模型 进行训练,利用所训练的模型,在获得 新的数据时 可以得到相应的输出。
线性模型的基本模型如下,其中的 ω \omega ω和 b b b是模型中的参数,训练模型的过程即为确定模型中参数的过程:
y ^ = ω x + b \widehat y=\omega x+b y =ωx+b
在本模型中设置成 y ^ = ω x \widehat y=\omega x y =ωx,对于不同的 ω \omega ω 有不同的线性模型及图像与之对应。

模型的训练过程:
在模型训练中 会先随机取得一个值,继而 计算其和标准量之间的 偏移量,从而判断 当前模型 是否符合预期。
记实际值为 y ( x ) y(x) y(x),模型对应的 预测值为 y ^ ( x ) \widehat y(x) y (x),则其中的 偏移量为 ∣ y ^ ( x ) − y ( x ) ∣ \left|\widehat y(x)-y(x)\right| ∣y (x)−y(x)∣,以此来代表 模型估计值 对原值的误差。
通常,该公式定义为Training Loss (Error)
l o s s = ( y ^ − y ) 2 = ( ω x − y ) 2 loss = (\widehat y - y)^2 = (\omega x - y)^2 loss=(y −y)2=(ωx−y)2
本例中,原题目中的几种 ω \omega ω所对应的Loss如下 几个图所示:
其中的每行 为 w w w不同时 的 单个样本的损失,最后一行为 平均损失。
对于单个样本,loss 可用于 指代样本误差。对于所有样本,可同理用Mean Square Error (MSE)来指代 整体样本的平均平方误差(均方差cost)
MSE:均方误差(Mean Square Error)。,即 每个样本对应的损失值 (平方) 求和,再除以样本总个数。
c o s t = 1 N ∑ n = 1 N ( y ^ n − y n ) 2 cost = \frac{1}{N} \displaystyle\sum_{n=1}^{N}(\widehat y_n-y_n)^2 cost=N1n=1∑N(y n−yn)2
ω = 3 \omega=3 ω=3:

ω = 4 \omega=4 ω=4:
![]()
ω = 2 \omega=2 ω=2: 可以看到 平均损失值为0
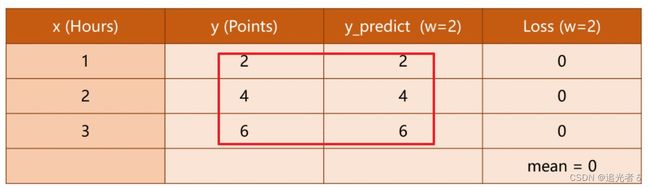
由cost的计算公式可知,当平均损失为0时,模型最佳,但由于 仅当数据无噪声 且 模型完美贴合数据 的情况下才会出现这种情况,因此 模型训练的目的 应当是 误差(损失)尽可能小,而非找到 误差为0的情况。
不同 ω \omega ω 得到的 MSE:
1.1.1 基础练习 y ^ = ω x \widehat y=\omega x y =ωx
根据上面的分析,code如下:注释我已经写的比较清楚啦。
# 昵 称:XieXu
# 时 间: 2023/2/12/0012 21:10
# 导入必要的工具包
import numpy as np
import matplotlib.pyplot as plt
# 自定义 简单数据集。x与y 一一对应 (训练集)
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
# 模型,(前馈)
def forward(x):
return x * w
# 损失函数
def loss(x, y):
y_pred = forward(x) # 即 y_hat。相当于 预测的值
return (y_pred - y) * (y_pred - y) # 平方(均方误差)。简单形式的均方误差。这个计算的 为单个样本的误差
# 【穷举法】
# 如下两个列表 保存 权重 及其对应的损失值
w_list = []
mse_list = []
# [0.0,4.1),间隔为0.1。即 0.0, 0.1, 0.2, 0.3 ... 4.0 起始值(含),停止值(不含),步长
for w in np.arange(0.0, 4.1, 0.1): # 外层循环 控制权重 2023.2.13 08:20
print("w=", w)
l_sum = 0
# zip 将x_data 和 y_data 打包为一个tuple(元组),方便同时遍历。
for x_val, y_val in zip(x_data, y_data): # 内层循环控制进行 权重: 调用forward函数 对应的预测,以及 调用上面定义的loss函数 进行损失值计算
y_pred_val = forward(x_val) # 计算 每个样本的 预测值
loss_val = loss(x_val, y_val) # 计算 每个样本的 损失值
l_sum += loss_val # 将 所有样本的 损失求和(这里没做均值)
print("\t", x_val, y_val, y_pred_val, loss_val) # 打印出 每一个样本:x,x对应的y,预测值y_hat,损失值
print("MSE=", l_sum / 3) # 这里 除以样本总数,进行均值,即 均方误差
w_list.append(w) # 将每次 用完的 权重添加到列表中,用以 下面画图 的横坐标~
mse_list.append(l_sum / 3) # 除以样本总数。 每个权重 对应的 所有样本的平均误差(均方误差) MSE,也叫均值吧。下面绘图的纵坐标
# 绘制图形
plt.plot(w_list, mse_list) # 横坐标、纵坐标 的取值
plt.ylabel("Loss") # 纵坐标y的标签
plt.xlabel("w") # 横坐标w的标签
plt.show()
可以得到结果:红色为我做的标注~
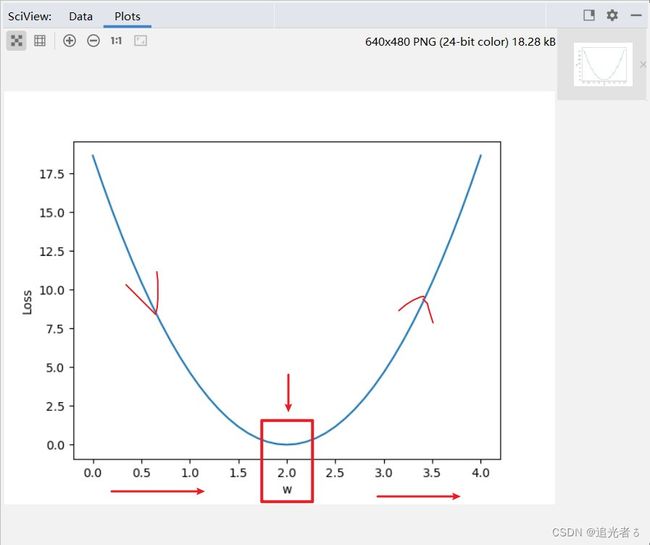
从下面 控制台打印的日志中,我们 可以 很容易看出来上图 的由来:
开始时,随着W增加,平均损失MSE逐渐减小,
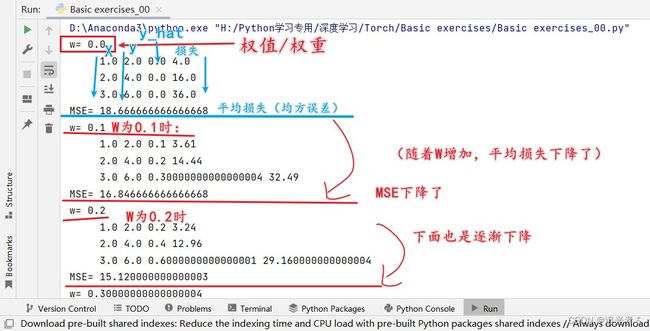
到W为2.0时,MSE达到最小 即0,

后面 W继续增加,MSE又变大了:
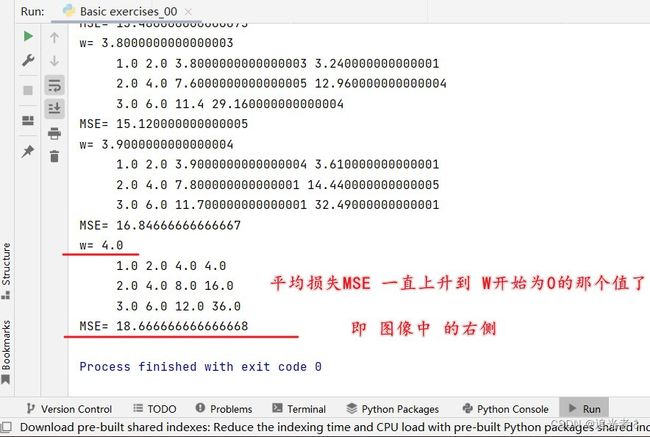
1.1.2 练习 y ^ = ω x + b \widehat y=\omega x+b y =ωx+b
同样地,基于上面的例子,练习:
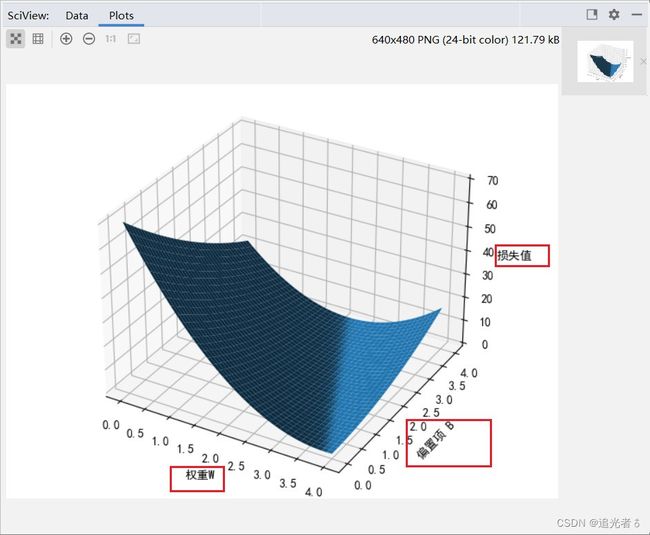
实现线性模型 y ^ = ω x + b \widehat y=\omega x+b y =ωx+b并输出loss的3D图像。
不同之处在于,定义的模型,与上面相比,加了个 偏置项B。
# 昵 称:XieXu
# 时 间: 2023/2/13/0012 12:26
# 练习题
# 作业题目:实现线性模型(y=wx+b)并画出loss的3D图像。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 以下两行代码 解决坐标轴不能显示中文问题 否则会报类似错误:FigureCanvasAgg.draw(self) (图上的 中文无法正常显示)
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
# 输入数据,设函数为y=3x+2
x_data = [1.0, 2.0, 3.0]
y_data = [5.0, 8.0, 11.0]
# 定义模型
def forward(x):
return x * w + b
# 定义损失函数
def loss(x, y):
y_pred = forward(x)
return (y_pred - y) * (y_pred - y)
mse_list = [] # 保存mse,均方误差
W = np.arange(0.0, 4.1, 0.1)
B = np.arange(0.0, 4.1, 0.1)
[w, b] = np.meshgrid(W, B) # 通过 两个坐标轴上的点 在平面上画网格
l_sum = 0
for x_val, y_val in zip(x_data, y_data):
y_pred_val = forward(x_val)
print(y_pred_val)
loss_val = loss(x_val, y_val)
l_sum += loss_val
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(w, b, l_sum / 3)
# 以下三行 设置坐标的文字说明
ax.set_xlabel("权重W")
ax.set_ylabel("偏置项 B")
ax.set_zlabel("损失值")
plt.show() # 画图
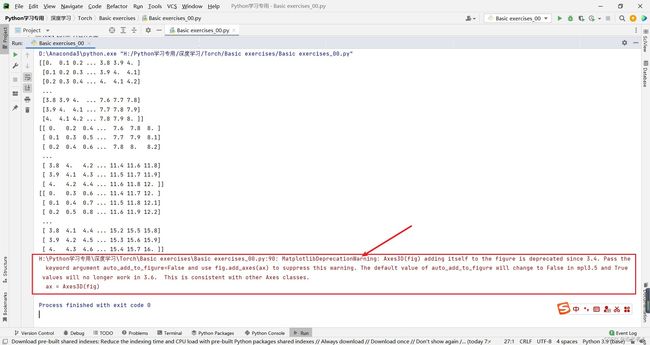
可以得到如下图形:这就是 ( y ^ = ω x + b \widehat y=\omega x+b y =ωx+b ) 损失值的3D图形。
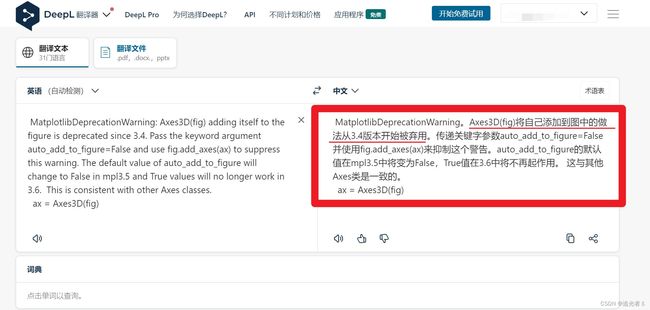
ax = Axes3D(fig)
翻译一下上面的警告:大意即 由于版本不同,可暂时忽略。
1.1.3 其它:在深度学习训练中,横轴往往是Epoch
在深度学习 训练 的可视化图形中,一般 横轴是Epoch,即训练轮数:往往在训练集上表现是,随着训练轮数增多,损失越来越低;而在测试集(老师读 开发集)上的效果是,损失 在刚开始会下降,而后 到某个点,又会逐渐上升。而我们的目标就是,想找到损失最低的那个点;从而进一步 对超参数进行处理等其它操作。
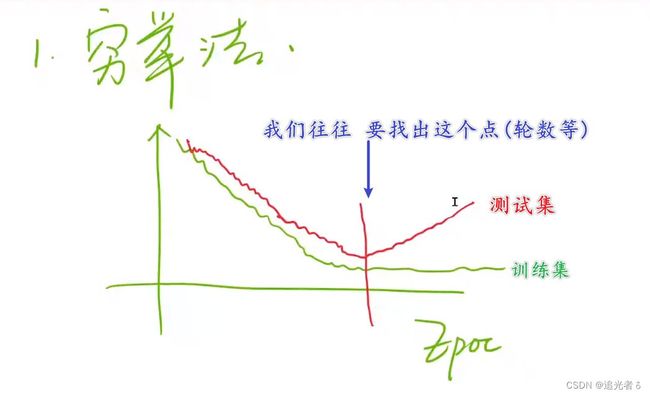
深度学习中可能需要考虑更多问题,比如 可视化问题 / 训练的时间问题(可能需要几天,甚至连续几周都是有可能的) / 断点问题(比如训练7天会结束,但是第6天程序崩溃了,这期间产生的数据 结果 怎么办)
老师提到了 Pytorch可视化工具——Visdom。目前我没有用到…稍微大型的项目可能会用到吧。可以在百度搜索Visdom并查看它的相关信息,以及其GitHub官网。
1.2 Gradient Descent(梯度下降)
1.2.1 梯度下降法 的由来:问题背景
在上面 线性模型的方法中,所使用的思想是基于穷举,即提前已经设定好 参数的准确值 在某个区间内并以某个步长进行穷举,如(np.arange(0.0,4.1,0.1))。
但是,这种思想 在多维的情况下,即多个参数的时候,会引起维度诅咒的现象,在一个N维曲面中找一个最低点,容易 使得原问题变得不可解。那么 既然有这样的问题,就需要对算法 进行改进。
那么,使用 分治法 如何?
即:大化小,小化无,先对整体 进行分割采样,在相对最低点进行进一步采样,直到其步长与误差符合条件。
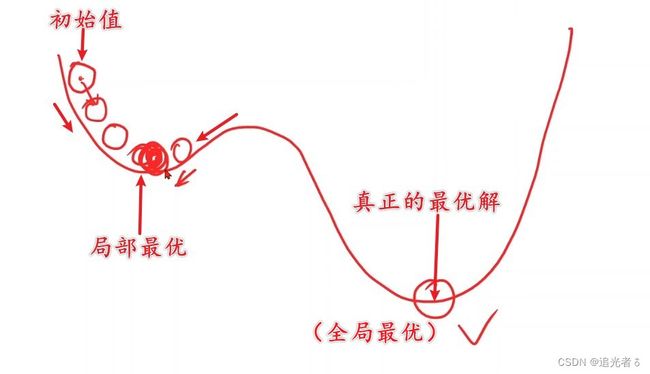
但是,分治法有两个缺点:
-
容易只找到
局部最优解,而不易找到一个全局最优解。 -
如果需要分得更加细致,则
计算量仍然巨大。
同时,由于以上问题的存在,引起了参数优化的问题,即求解使loss最小时的参数的值。
简言之,即求得 ω \omega ω,使得loss值最小。
ω ∗ = arg min ω c o s t ( ω ) \omega ^* = \mathop{\arg\min}_\omega cost(\omega) ω∗=argminωcost(ω)
如何优化,求得符合条件的 ω \omega ω呢?
1.2.2 何为梯度?
梯度,即 导数变化最大的值,其方向为导数变化最大的方向。
这里,可以使用高等数学中关于 一个点处 导数的定义:
∂ f ∂ x = lim △ x → ∞ f ( x + △ x ) − f ( x ) △ x \frac{\partial f}{\partial x}=\lim_{\triangle x\rightarrow\infty}\frac{f(x+\triangle x)-f(x)}{\triangle x} ∂x∂f=△x→∞lim△xf(x+△x)−f(x)
(这里仅简单理解,并非严谨数学推导)对于 △ x \triangle x △x,若增函数,梯度为上升方向,若减函数,梯度为下降方向。由数学知识 知道,需要取梯度下降的方向 即梯度的反方向作为变化方向,才能尽可能地求得极小值(最小值)。
下面的图将便于理解:
1.2.3 梯度下降
在深度学习中,所说的凸函数,是与高等数学定义中的 凸函数,完全反过来的,知道这一点就好。如下图所示,在深度学习中,将其看做一个凸函数。
当前, W W W的取值点 与 全局最小值点:
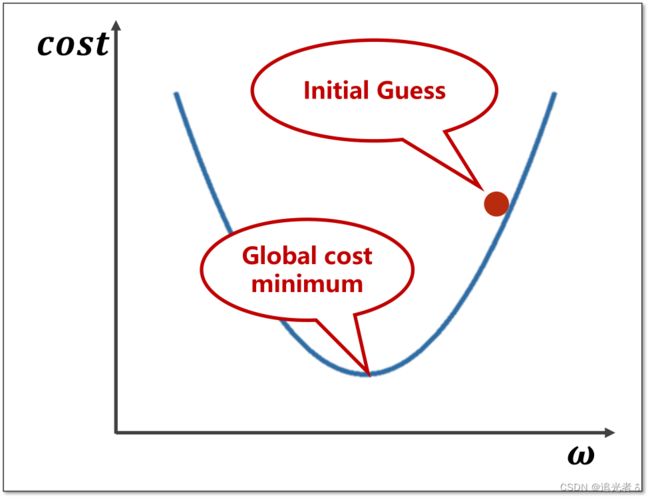
那么,取值点 需要 向下更新,所取的梯度即为 ∂ c o s t ∂ ω \frac{\partial cost}{\partial \omega} ∂ω∂cost,更新的公式如下,其中 α \alpha α为 学习率,即 所下降的步长,不宜取太大。
ω = ω − α ∂ c o s t ∂ ω \omega = \omega - \alpha \frac{\partial cost}{\partial \omega} ω=ω−α∂ω∂cost
- [1] 梯度下降算法 容易进入
局部最优解(非凸函数),但是实际问题中的局部最优点较少,或 已经基本可以当成全局最优点。
- [2] 梯度下降算法容易陷入
鞍点(鞍点处,梯度值为0)(总之不是取得 损失最小值的点,简单理解为 局部最优:在优化问题中,鞍点 是一种特殊的局部最优解,是一个难以优化的点,因为优化算法 可能 很难从鞍点 附近找到 全局最优解)。(陷入到鞍点,导致无法继续 进行迭代!)
1.2.4 梯度下降的公式 如何得来的?(理解)
通过线性模型,我们知道 均方误差的公式即:其中 ( y ^ = ω x \widehat y=\omega x y =ωx)
c o s t = 1 N ∑ n = 1 N ( y ^ n − y n ) 2 cost = \frac{1}{N} \displaystyle\sum_{n=1}^{N}(\widehat y_n-y_n)^2 cost=N1n=1∑N(y n−yn)2
进一步地,可以对 ω \omega ω求偏导,一步一步来:
∂ c o s t ( w ) ∂ ω = ∂ ∂ w 1 N ∑ n = 1 N ( y ^ n − y n ) 2 \frac{\partial cost(w)}{\partial \omega} = \frac{\partial}{\partial w} \frac{1}{N} \displaystyle\sum_{n=1}^{N}(\widehat y_n-y_n)^2 ∂ω∂cost(w)=∂w∂N1n=1∑N(y n−yn)2
∂ c o s t ( w ) ∂ ω = ∂ ∂ w 1 N ∑ n = 1 N ( ω x n − y n ) 2 \frac{\partial cost(w)}{\partial \omega} = \frac{\partial}{\partial w} \frac{1}{N} \displaystyle\sum_{n=1}^{N}(\omega x_n-y_n)^2 ∂ω∂cost(w)=∂w∂N1n=1∑N(ωxn−yn)2
1 N \frac{1}{N} N1是常数,对求 ω \omega ω的导数没有影响,可以提到前面来:
∂ c o s t ( w ) ∂ ω = 1 N ∑ n = 1 N ∂ ∂ w ( ω x n − y n ) 2 \frac{\partial cost(w)}{\partial \omega} =\frac{1}{N} \displaystyle\sum_{n=1}^{N}\frac{\partial}{\partial w}(\omega x_n-y_n)^2 ∂ω∂cost(w)=N1n=1∑N∂w∂(ωxn−yn)2
根据数学知识,由于是对 ω \omega ω求导,那么 可以 把 ( ω x n − y n ) (\omega x_n-y_n) (ωxn−yn)看做一个整体,【复合函数求导】:对含有 ω \omega ω的 (外部)整体 求导,乘以内部 对 ω \omega ω求导,故而得:
∂ c o s t ( w ) ∂ ω = 1 N ∑ n = 1 N 2 ( x n ω − y n ) ∂ ( x n ω − y n ) ∂ w \frac{\partial cost(w)}{\partial \omega} =\frac{1}{N} \displaystyle\sum_{n=1}^{N}2(x_n \omega-y_n)\frac{\partial(x_n \omega - y_n)}{\partial w} ∂ω∂cost(w)=N1n=1∑N2(xnω−yn)∂w∂(xnω−yn)
而 ( ω x n − y n ) (\omega x_n-y_n) (ωxn−yn) 对 ω \omega ω求导的结果 显然为 x n x_n xn,调整一下顺序,就得到对 ω \omega ω的最终求导结果:
∂ c o s t ( w ) ∂ ω = 1 N ∑ n = 1 N 2 x n ( x n ω − y n ) \frac{\partial cost(w)}{\partial \omega} =\frac{1}{N} \displaystyle\sum_{n=1}^{N}2 x_n(x_n \omega - y_n) ∂ω∂cost(w)=N1n=1∑N2xn(xnω−yn)
因此,梯度下降的更新公式为:
ω = ω − α 1 N ∑ n = 1 N 2 x n ( x n ω − y n ) \omega = \omega - \alpha \frac{1}{N} \displaystyle\sum_{n=1}^{N}2 x_n(x_n \omega - y_n) ω=ω−αN1n=1∑N2xn(xnω−yn)
下图即上述公式的推导过程:
梯度的求解公式,应用到code中的示例:
![]()
1.2.5 随机梯度下降(Stochastic gradient descent,SGD);Mini-batch!
平时用的比较多的,是 随机梯度下降(SGD)。
SGD采用单个训练样本的损失来近似平均损失,故 SGD 用单个训练数据即可对模型参数进行一次更新,大大加快了训练速度。
随机梯度下降 每次 只需要计算 一个样本 关于 W W W的导数:
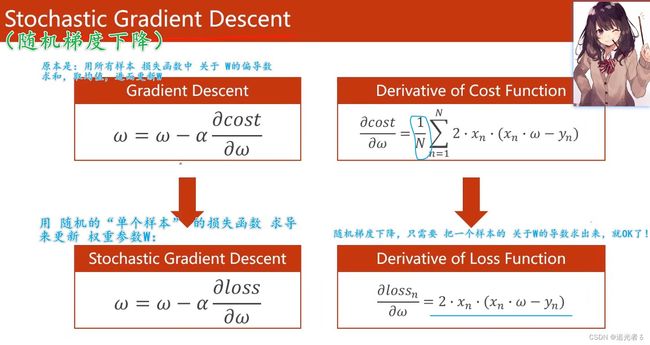
随机梯度下降SGD 与 标准梯度下降的区别:
-
标准梯度下降 在权值更新前 汇总
所有样例得到的标准梯度,随机梯度下降 则是通过考察每次训练实例来更新。 -
标准梯度下降的是使用准确的梯度,理直气壮地走,随机梯度下降使用的是近似的梯度,小心翼翼地走。
-
标准梯度下降的步长 比 随机梯度下降 的大。
-
当有多个局部极小值时,随机梯度 反而更可能 避免 进入局部极小值中。
同时,为了降低随机梯度的方差,使迭代算法更加稳定,在真实操作中,会同时处理若干训练数据,该方法叫做小批量随机梯度下降法(Mini_Batch Gradient Densent)。,这才是真正地运用了 随机梯度下降(SGD),目前,在实际应用中,我们所说的梯度下降,(batch)都是指的 Mini-batch SGD,小批量 随机梯度下降。 这在神经网络中,尤其明显!!!使用及其广泛!!!(既 保证 性能,又保证时间复杂度不是特别高)
小结
普通梯度下降算法利用数据整体,不容易避免鞍点,
算法性能欠佳,但算法效率高。随机梯度下降需要利用每个的单个数据,虽然算法性能良好,但计算过程 环环相扣 无法将样本抽离开 并行运算,因此算法效率低,时间复杂度高。
综上所述,可采取一种折中的方法,即批量梯度下降方法。
将若干个样本分为一组,记录一组的梯度 用以代替随机梯度下降中的单个样本。
该方法最为常用,也是默认接口。一般,mini-batch可以在2的幂次中挑选最优取值。例如16、32、64、128、256等。
1.2.6 梯度下降练习:方法一(推荐 完全 自己 多手写几遍)
给定一个数据集,x_data、y_data。寻找y=wx模型的w最优解。
code练习如下,注释中,我已经介绍的比较详细啦!我想这可以帮助绝大多数朋友理解。
# 昵 称:XieXu
# 时 间: 2023/2/13/0013 13:26
# 梯度下降算法
# 注:在 深度学习算法 中,并没有过多的局部最优点。
# 即 一般 通过梯度下降 就可以求得 最优点
import numpy as np
import matplotlib.pyplot as plt
# 训练数据,x与y一一对应
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
epoch_list = [] # # 2023.2.13 13:58 保存训练轮数
cost_list = [] # 2023.2.13 13:58 每一轮对应的损失值
w = 1.0 # 初始化,我们指定一个W取值
# 前馈计算(定义模型)
def forward(x):
return x * w
# 求MSE (定义cost函数,计算均方误差)
def cost(xs, ys):
cost = 0
for x, y in zip(xs, ys):
y_pred = forward(x)
cost += (y_pred - y) ** 2
return cost / len(xs) # 计算 均方误差(损失)
# 求梯度(求W的偏导数)
def gradient(xs, ys):
grad = 0
for x, y in zip(xs, ys):
temp = forward(x)
grad += 2 * x * (temp - y) # 由导数公式得
return grad / len(xs)
print("Predict(before training)", 4, forward(4)) # 这是根据 我们 给定的那个W,计算y=wx得到的值,forward(4) 即4
# 开始训练
for epoch in range(1, 101, 1):
cost_val = cost(x_data, y_data) # 计算均方误差(损失)
grad_val = gradient(x_data, y_data) # 求梯度(W的偏导数)
w -= 0.01 * grad_val # 梯度下降,更新梯度(W)
print("Epoch: ", epoch, "w = ", w, "loss = ", cost_val) # w就会用在下一轮的训练中
epoch_list.append(epoch) # 保存轮数1~100,做绘图的横坐标
cost_list.append(cost(x_data, y_data)) # 每轮对应的 损失值
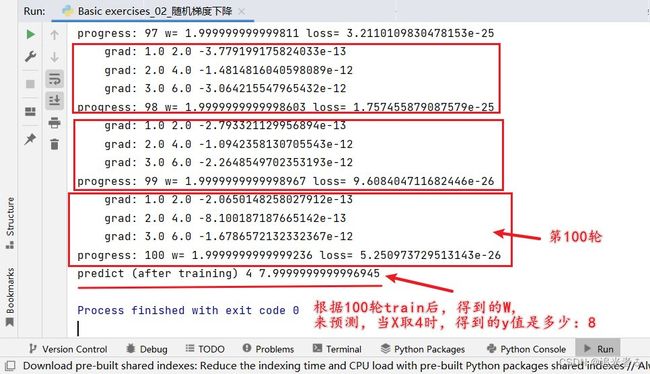
print("Predict(after training)", 4, forward(4)) # 根据100轮 之后的权重W,计算x取4时,预测的y值。实际应该是无限接近2,即2
# 绘图
plt.plot(epoch_list, cost_list) # 横坐标 和 纵坐标 分别是 轮数 和 对应该轮的 损失值
plt.title("train loss")
plt.xlabel('Epoch')
plt.ylabel("Cost")
plt.show()
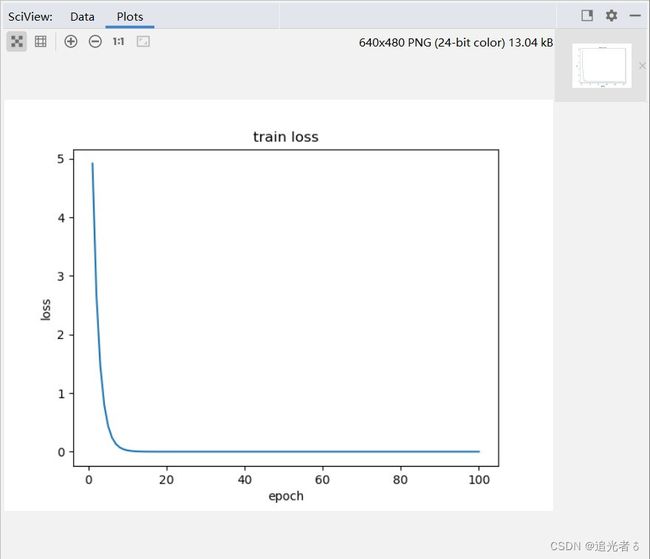
得到结果:可以看到,在20轮左右,损失值就已经很接近0了。
![]()
控制台的结果:为了便于展示,这里我也特意截取到了20轮的训练结果。
1.2.7 方法二(与法一类似,不过这里 纵轴 是 权值的 收敛变化 收敛变化 收敛变化)
第二种方式:与第一种类似,只不过这里纵坐标取的是 权值,另外,直接把梯度下降 放到Epoch训练里面了。代码如下:
# 方法二
import numpy as np
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
scope_list = [] # 轮数
w_list = [] # 权值W
w = 60 # 我们给W一个初始值
# 学习率
k = 0.01 # 定义学习率
# 开始训练
for i in range(1,201,1):
# 计算cost(loss的和)
loss_sum = 0
# 求梯度
for x_val, y_val in zip(x_data, y_data):
loss_sum += 2 * x_val * (w * x_val - y_val)
cost = loss_sum / 3
# 计算本轮w
w = w - k * cost
print("Epoch:",i,"W:",w)
scope_list.append(i)
w_list.append(w)
# 按说纵坐标不应该取权值的,既然取了,那么可以从图形中,看出来大概 50左右,权值就收敛了
plt.plot(scope_list, w_list) # 横坐标 取值 依然是 轮数,纵坐标取值是按照W来取的值
plt.xlabel("scope")
plt.ylabel("W")
plt.show()
结果如下所示:
我们也可以看一下,Console控制台输出的内容:可以看到,50多轮依然还在收敛,100轮左右就已经收敛的比较好了~ 最终权值 W W W应为2
1.2.8 随机梯度下降练习(一),可视化
这里,即 普通的 随机梯度下降,每轮训练中,每次计算的 关于 W W W的 偏导数,是仅仅 只计算 一个样本的,而非 所有样本的 关于 W W W的偏导数 求和 再取均值。
即 注:这里,随机梯度主要是指,每次拿一个训练数据来训练,然后更新梯度参数。
# 昵 称:XieXu
# 时 间: 2023/2/13/0013 15:11
# 随机梯度下降
# 方法一
# 注:这里,随机梯度主要是指,每次拿一个训练数据来训练,然后更新梯度参数。
# 本算法中 梯度总共更新100(epoch)x3 = 300次。梯度下降算法中 梯度总共更新100(epoch)次。
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = 1.0
def forward(x):
return x * w
# calculate loss function(损失函数--均方误差)
def loss(x, y):
y_pred = forward(x)
return (y_pred - y) ** 2 # 仅 计算一个样本 的损失函数
# define the gradient function sgd(定义随机梯度下降 函数)
def gradient(x, y):
return 2 * x * (x * w - y) # 注:这里,仅计算 “一个样本” 关于W 的 偏导数
epoch_list = [] # 训练轮数,100轮 2023.2.13 19:24
loss_list = []
print('predict (before training)', 4, forward(4))
for epoch in range(1, 101, 1):
for x, y in zip(x_data, y_data):
grad = gradient(x, y) # 这里,每轮训练中,三个 样本中 都分别计算了 梯度,for...zip循环。 应该是没有用到“随机”
w = w - 0.01 * grad # update weight by every grad of sample of training set。根据梯度,更新W。。。
print("\tgrad:", x, y, grad) # 打印每轮训练中,每个样本的x、y、根据其计算的梯度。 2023.2.13 19:36
l = loss(x, y) # 根据梯度得到的 更新后的W,进一步 计算损失函数(均方误差) 2023.2.13 19:36
print("progress:", epoch, "w=", w, "loss=", l) # 打印该轮中,通过每一个样本 得到的 W 以及 损失函数值!!!2023.2.13 19:37
epoch_list.append(epoch)
loss_list.append(l)
print('predict (after training)', 4, forward(4))
plt.plot(epoch_list, loss_list)
plt.title("train loss")
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()
1.2.9 随机梯度下降练习(二),可视化
上面的随机梯度下降算法中,貌似仅仅 是只计算了 每一个样本的梯度,好像没有体现“随机”。
这里再换个类似的算法,基本一样,但用到了random随机。
该方法与目录1.2.6类似。
# 方法二
import random
import numpy as np
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
scope_list = [] # 训练轮数
w_list = [] # 权值
w = 60
# 学习率
k = 0.01
for i in range(1, 201, 1):
# 计算cost(即随机一个loss当cost用)
rand = random.randint(0, 2) # 取值为[0,2],即 随机生成0~2内的 某个 整数,包含0和2。(三个样本,随机取一个)
cost = 2 * x_data[rand] * (w * x_data[rand] - y_data[rand]) # 从而计算得到 关于W的偏导数
# 计算本轮w
w = w - k * cost # 更新W
print("Epoch=", i, "W=", w) # 本轮更新后的W 2023.2.13 20:30
scope_list.append(i)
w_list.append(w)
plt.plot(scope_list, w_list) # 横坐标为轮数,纵坐标为权值。
plt.xlabel("scope")
plt.ylabel("W")
plt.show()
1.3 反向传播(Back Propagation)
1.3.1 从 神经网络视角下 来看:
Back Propagation算法 是神经网络中很重要的一个算法。可以在图上 进行梯度的传播。这里用到的核心知识,我认为依然是计算图。
在线性模型 y ^ = ω x \widehat y = \omega x y =ωx中,若以神经网络的视角代入来看,则 x x x为输入层,即input层, ω \omega ω为权重, y ^ \widehat y y 为输出层。
在神经网络中,通常将 ω \omega ω以及 ∗ * ∗计算操作的部分 合并 看做一个神经元(层)。而神经网络的训练过程即为更新 ω \omega ω的过程,注意:其更新的情况依赖于 ∂ l o s s ∂ ω \frac{\partial loss}{\partial \omega} ∂ω∂loss,而并非 ∂ y ^ ∂ ω \frac{\partial \widehat y}{\partial \omega} ∂ω∂y .
神经网络 视角下的 线性模型 示意图:
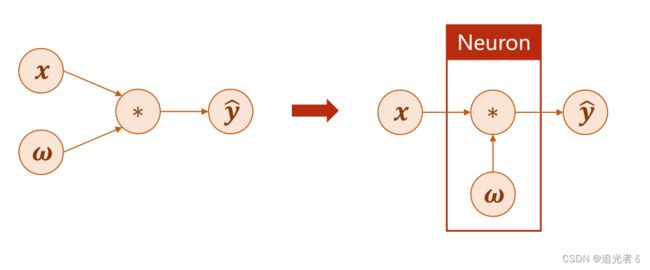
可是,对于复杂模型而言 求解过程就复杂很多。在图示的神经网络中,每个结点为一个神经元,结点之间的连线为权重。这里,各个符合 及其 表示的含义 如下表格所示:关键词为 层、权重(权值)、输入层、输出层、隐含层。
| 符号 | 表示的含义 |
|---|---|
| x i x_i xi | 输入层的第i个节点 |
| h i j h_{ij} hij | 第i层隐含层的 第j个节点 |
| o i o_i oi | 输出层的第i个节点 |
| ω x 1 m n \omega_{x1}^{mn} ωx1mn | 输入层的第m个结点 与 隐含层的第n个结点之间的权重 |
| ω i j m n \omega_{ij}^{mn} ωijmn | 隐含层第i层的 第m个节点 与 第j层的第n个节点 之间的权重 |
| ω k o m n \omega_{ko}^{mn} ωkomn | 隐含层最后一层(第k层) 的第m个节点 与 输出层第n个节点 之间的权重 |
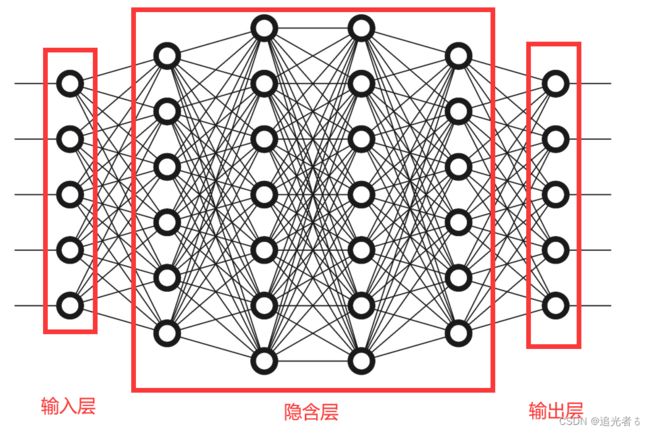
如下图所示,输入层 与隐含层第一层 之间就有 5 ∗ 6 = 30 5*6=30 5∗6=30个权重,隐含层的第一层与第二层之间又有 6 ∗ 7 = 42 6*7=42 6∗7=42个权重,以此类推,上图中共有 30 + 42 + 49 + 42 + 30 = 193 30+42+49+42+30=193 30+42+49+42+30=193个权重需要计算,传统的 写解析式的方式 是难以完成 (无法完成)的。
1.3.2 “计算图” 中的 神经网络;由 单纯添加层数的“无效复杂” 到 添加 非线性激活函数(如sigmoid/ReLU/等)后的“有效复杂”
在下图右侧的计算图中,绿色的模块为计算模块,可以在计算过程中求导。MM为矩阵乘法(Matrix Multiplication),ADD表示加法运算。简单来说 即 权重 W W W与输入层 X X X 做矩阵乘法运算,得到的结果 再与 偏置项 b b b进行 向量加法运算。因此 b b b通常是向量的形式,一列 / 一行。

上图左侧公式中,可以化简得到如下公式:
y ^ = W 2 ( W 1 X + b 1 ) + b 2 = W 2 W 1 X + ( W 2 b 1 + b 2 ) = W X + b \widehat y = W_2(W_1X+b_1)+b_2=W_2W_1X+(W_2b_1+b_2)=WX+b y =W2(W1X+b1)+b2=W2W1X+(W2b1+b2)=WX+b
也就是说,在这个结构下 单纯地增加层数,并不能增加神经网络的复杂程度,因为最后都可以化简为一个单一的神经网络。
下图即:神经网络的“无效复杂”,
方法是:在每层网络结构中,增加一个 非线性的变换函数(激活函数)
增加激活函数后的神经网络:
![]()
如 添加sigmoid激活函数(或其它非线性激活函数 如ReLU激活函数):(注:这里,下边的 本小节code练习中并未用到sigmoid,因为模型简单,并不需要搭建神经网络. 在 目录1.5的逻辑回归(以二分类为例)中将会正式介绍sigmoid激活函数!)【添加激活函数后 才是真正的神经网络!】

(有同学说:加了激活函数后,神经网络才有了 能够逼近 任意函数形式的能力~)
1.3.3 反向传播的过程;前馈计算,反向传播!
前馈计算
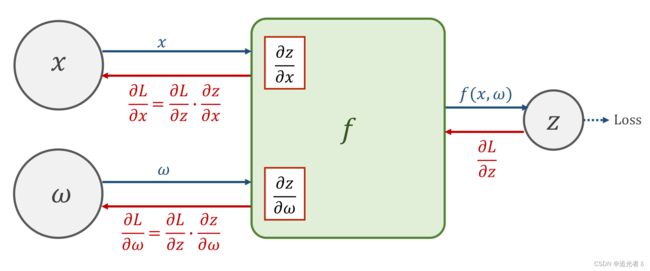
在某一神经元处,输入的 x x x与 ω \omega ω经过函数 f ( x , ω ) f(x,\omega) f(x,ω)的计算,可以获得输出值 z z z,并继续向前以得到损失值loss。
在向前计算的过程中,在 f ( x , ω ) f(x,\omega) f(x,ω)的计算模块中 会计算导数 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z以及 ∂ z ∂ ω \frac{\partial z}{\partial \omega} ∂ω∂z,并将其保存下来(在pytorch中,这样的值保存在变量 x x x以及 ω \omega ω中)。
前馈计算过程:沿着箭头方向,先去计算最终的Loss。这一过程中,计算 f f f时就能顺便把 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z 和 ∂ z ∂ ω \frac{\partial z}{\partial \omega} ∂ω∂z给求出来(为反向传播时的计算 做准备)。(注:为何也要求出 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z?这是因为 除输入层外, x x x 也很有可能是 中间结果,如 x x x是上一层的输出,此时 就对 Z Z Z有需求了)
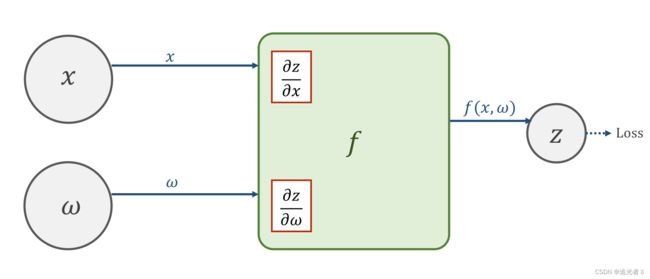
反向传播
(根据链式求导法则),求得loss以后,前面的神经元会将 ∂ l o s s ∂ z \frac{\partial loss}{\partial z} ∂z∂loss的值反向传播给原先的神经元,在计算单元 f ( x , ω ) f(x,\omega) f(x,ω)中,将得到的 ∂ l o s s ∂ z \frac{\partial loss}{\partial z} ∂z∂loss与之前存储的导数( ∂ z ∂ ω \frac{\partial z}{\partial \omega} ∂ω∂z、 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z)分别 相乘,即可得到损失值对于 权重以及输入层的导数,即 ∂ l o s s ∂ x \frac{\partial loss}{\partial x} ∂x∂loss,以及 ∂ l o s s ∂ ω \frac{\partial loss}{\partial \omega} ∂ω∂loss.基于该梯度才进行权重的调整。
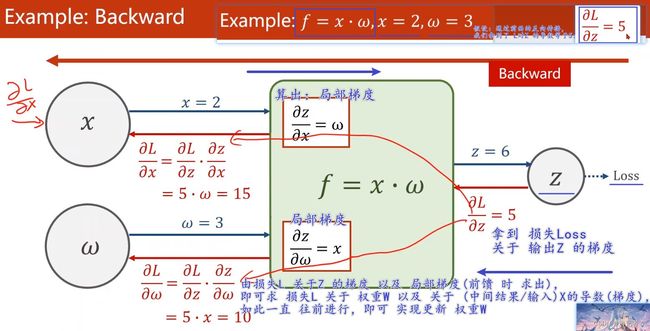
举个实际的例子,如下图,假设 f = x ⋅ ω f=x·\omega f=x⋅ω,且 x = 2 , ω = 3 x=2,\omega=3 x=2,ω=3,已经求得 损失L 对 输出Z的导数值为5,那么计算过程即如下所示:
这样我们就得到了 相应的导数(损失 L L L关于权重 W W W的导数),就可以去做 权重 W W W的更新了!
再举个例子:
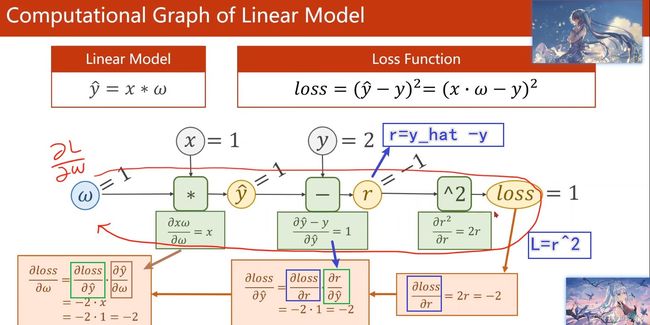
练习题1:这里若 x = 2 , w = 1 , y = 4 x=2,w=1,y=4 x=2,w=1,y=4:那么前馈计算 与 反向传播的计算如下:我想我写的比较清楚叭!建议大家也手推一遍~
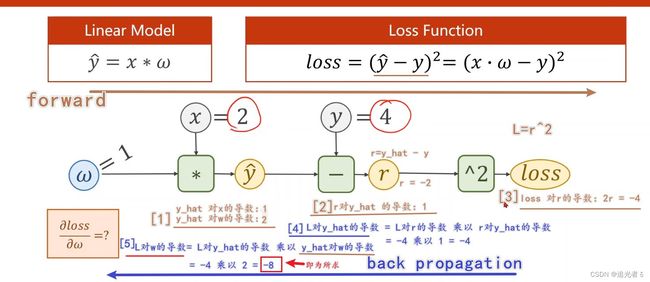
练习题2:当为 y ^ = ω x + b \widehat y=\omega x+b y =ωx+b,且 w = 1 , x = 1 , b = 2 , y = 2 w=1,x=1,b=2,y=2 w=1,x=1,b=2,y=2时:
这里我建议大家 自己手推一遍哈!
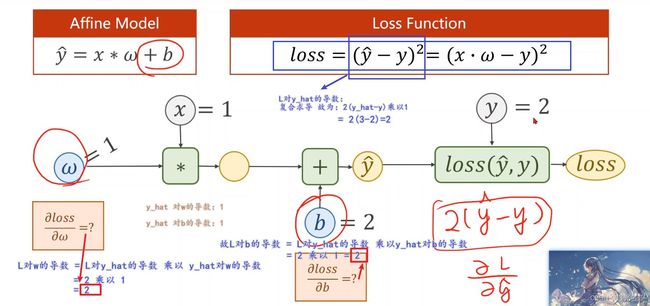
(可能有同学会说:反向传播 计算Loss 对每个 ω \omega ω的梯度,然后更新 ω \omega ω 来进行 “梯度下降”,降低Loss;;;“前馈计算loss,反馈计算权值”;;)
1.3.4 附:PyTorch中的 前馈与反馈;Tensor!
通过pytorch进行 深度学习 基础模型的构建,最主要的是构建计算图。
“张量”
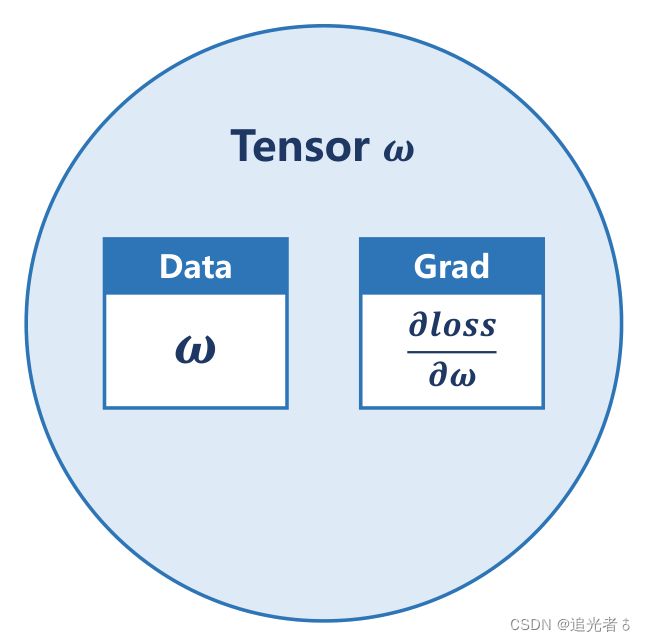
Tensor中,可以存标量、向量、矩阵,亦有高维度的Tensor。Tensor是一个类。
Tensor中的两个重要成员 是 data 和 grad。data用于保存 权重本身的值 ω \omega ω,grad用于保存 损失函数对权重的导数 ∂ l o s s ∂ ω \frac{\partial loss}{\partial \omega} ∂ω∂loss,grad本身也是个张量。对张量进行的计算操作,都是建立计算图的过程。
关于Tensor的小练习,未来我会抽时间记录。
1.3.5 PyTorch反向传播练习(1) y ^ = ω x \widehat y=\omega x y =ωx
- 先算损失
- 然后,反向传播
- 有了梯度,就可以 用梯度下降 进行(权重) 更新
该小节的代码,注释我依然写的是比较详细的,另外,建议结合以下几张图,会理解的更深刻一些~


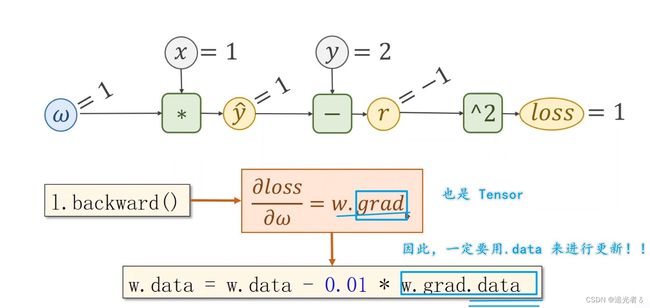
阅读code时,建议看下注释,你会理解的 ♪(^ ∇ ^*)~
# 昵 称:XieXu
# 时 间: 2023/2/14/0014 17:47
import torch
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = torch.tensor([1.0]) # 设置tensor中的data(数据。。),即 w的初值为1.0
w.requires_grad = True # 指定w是需要计算梯度的!!(因为 默认不指定的话,是不会计算w的梯度的)2023.2.14 19:13
def forward(x):
# 这里 x与w要进行 【数乘】 运算;而w是一个Tensor,
# 因此,x要进行 自动类型转换,把它转换成一个Tensor!
return x * w # 注意!!!! w是一个Tensor
# x和w进行 乘法运算,得到相应地输出,构建了【计算图】
# w是需要计算梯度的,因此 x*w 运算得到的结果 也需要计算梯度
# 每调用一次loss函数,就动态地【构建了】一次 【计算图】
def loss(x, y):
y_pred = forward(x) # 得到 y_hat
return (y_pred - y) ** 2 # 计算损失
print("predict (before training)", 4, forward(4).item())
for epoch in range(1, 101, 1):
for x, y in zip(x_data, y_data): # (每次都 随机梯度下降SGD~) 把x_data 和 y_data zip成 一个数据~
# 前馈的过程,你只需要计算loss ## 即 创建【新的】计算图 2023.2.14 20:49
l = loss(x, y) # loss是一个“张量”,tensor主要是在建立计算图 forward, compute the loss
# 调用张量l的 成员函数backward(), 它就会自动地把 计算链路上(刚刚 画的【计算图】上) 所有的需要梯度的地方,把梯度 都求出来
# 求完之后,把梯度 都存到变量里边,如 这里是把梯度 都存到w里面。
# 存到w里面之后,实际上 计算图 就被释放了。“只要一做backward,这个计算图就被释放了!这个计算图就没有了”
# 那么下一次,再进行loss计算的时候,会创建一个 新的计算图
# ### 进行反馈计算,此时才开始求梯度,此后 之前的计算图进行释放!!! 2023.2.14 20:48
l.backward() # backward,compute grad for Tensor whose requires_grad set to True
print('\tgrad:', x, y, w.grad.item()) # .item() 是 把梯度的数值 直接拿出来,变成Python中的标量【###即 grad.item()取grad中的值变成标量】
# 注:grad也是一个tensor。
# # # #必须要 取到grad的data,即 (w.grad).data。 如果是 w.data - 0.01 * w.grad,那这就是 在建立计算图,而不是更新权重。
# 取张量的data来计算,好处 是 它是不会建立计算图的!
# (构建计算图的时候 使用张量就可,但是权重更新的时候,要使用data!)### 即 单纯的数值计算要利用data,而不能用张量,否则会在内部创建新的计算图
w.data = w.data - 0.01 * w.grad.data # 权重更新时,注意“grad也是一个tensor!!!” 。。。这里做的就是对 权重w 纯数值的更新(修改)
# 有同学说 w.data相当于 requires_grad=False的w,但是与requires_grad=True的w共享数据,这是为了节省空间
# # # # 以下code,意为把权重里面 梯度的数据 全都清零!
# 因为,上面把w即权重更新完之后,L关于w的 梯度(导数)还在。如果不清零,那么下一次运算,会把之前L关于w的导数 加到一起..
# 即:如果想要w的梯度(导数)清零,必须显示地 写明 清零的语句~
w.grad.data.zero_() # after update, remember set the grad to zero
print('progress:', epoch, l.item()) # 取出loss使用l.item,不要直接使用l(l是tensor会构建计算图)
print("predict (after training)", 4, forward(4).item())
附:便于理解~(2023.2.17 23:31)
1.3.6 PyTorch反向传播练习(2) y ^ = ω 1 x 2 + ω 2 x + b \widehat y=\omega_1 x^2 + \omega_2x + b y =ω1x2+ω2x+b
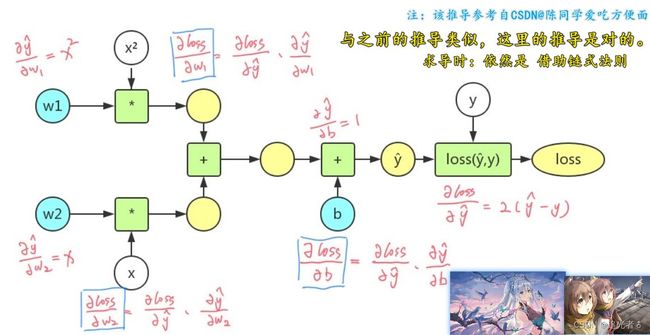
题目如下,需要求解三个梯度(导数):

推导过程:我没有平板,公式就不好直接写了,找了一个例子如下,推导过程 应该是没问题的。
# 昵 称:XieXu
# 时 间: 2023/2/14/0014 21:56
# y=w1x²+w2x+b
import numpy as np
import matplotlib.pyplot as plt
import torch
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
# 声明w1、w2、b为Tensor,并赋予初值 且指定 都需要计算梯度
w1 = torch.Tensor([1.0]) # 初始权值
w1.requires_grad = True # 计算梯度,默认是不计算的,因此这里需要手动指定为True,即 要计算梯度。 如下亦同理
w2 = torch.Tensor([1.0])
w2.requires_grad = True
b = torch.Tensor([1.0])
b.requires_grad = True
def forward(x):
return w1 * (x ** 2) + w2 * x + b # 注:w1 w2 b 三者 都是Tensor
def loss(x, y): # 构建计算图
y_pred = forward(x)
return (y_pred - y) ** 2
# print('Predict (befortraining)', 4, forward(4)) # 不加.item()的话,那么结果 就成Tensor啦! 取值,需要通过 .item() 2023.2.14 22:18
print('Predict (befortraining)', 4, forward(4).item()) # 未预测之前 ,通过我们上面给出的默认的w1,w2和b 计算的结果:16+4+1=21
# 注:学习率为0.01时,5000轮 结果为8.03 或 10000轮 结果为8.002 效果 都会比较好一些 2023.2.14 22:13
# 训练100次后可以看到当x=4时,y=8.544,与正确值8相差比较大。 原因是α=0.01取值过小,可以取 α=0.02,那么100轮后结果 8.06
for epoch in range(1, 101, 1):
# l = loss(1, 2) # 为了在for循环之前定义l,以便之后的输出,无实际意义
for x, y in zip(x_data, y_data):
l = loss(x, y) # 前馈过程,计算损失
l.backward() # 反馈过程,反向传播,求解梯度。w1 w2 b的梯度都会计算出来
print('\tgrad:', x, y, w1.grad.item(), w2.grad.item(), b.grad.item()) # 注意是通过.item() 即 将梯度 转换为标量 打印出来 值
# 更新w1 w2 b,注意 取值要从data取
w1.data = w1.data - 0.01 * w1.grad.data # 注意 这里的grad是一个tensor,所以要取它的data,下亦 同理
w2.data = w2.data - 0.01 * w2.grad.data
b.data = b.data - 0.01 * b.grad.data
w1.grad.data.zero_() # 释放之前计算的梯度。下亦同理
w2.grad.data.zero_()
b.grad.data.zero_()
print('Epoch:', epoch, l.item()) # 取出本轮的损失值,注意 也是通过.item()来取 2023.2.15 07:55
# print('Epoch:', epoch, l) # tensor([0.0063], grad_fn=),这样是张量,通过item才能取到其 值
print('Predict(after training)', 4, forward(4).item())
注意,这是当Epoch为100轮,学习率为0.01时的结果:当x为4时,最后y取值为8.5,与正确值8 误差还是比较大的!
w1.data = w1.data - 0.02 * w1.grad.data
w2.data = w2.data - 0.02 * w2.grad.data
b.data = b.data - 0.02 * b.grad.data
结果是8.06,已经比较接近8了:
学习率仍然设置为0.01,轮数设置为5000轮:8.03,结果更接近8了,更精准了:

学习率还是不变,为0.01,训练10000轮:结果是8.002,更接近8了。

这可能是由于模型 比之前设置的 要复杂一些,因此在超参数的调整上,如学习率不能太小,这里0.01就显得有些小了,可以试试0.02等;训练轮数不能太少等等这些因素都有关系。当然,使用的数据 显然是一次函数的数据,要拟合二次函数模型(非线性 模型),确实要费些力气。【多调试一下参数,如尝试增大学习率 / 增加训练轮数 等】
附:便于理解~ (2023.2.17 23:28)
![]()
1.3.7 补充——针对1.3.5,可视化,看权重收敛情况。 y ^ = ω x \widehat y=\omega x y =ωx
与目录1.3.5 类似,这里拟合的模型依然是线性模型 y ^ = ω x \widehat y=\omega x y =ωx,直接把 求损失函数 写在 训练过程里了,同时为了看出权重 w w w的收敛情况,给它设定初值66,大一些。
# 昵 称:XieXu
# 时 间: 2023/2/15/0015 8:26
# 也是拟合y=w*x,
# 【反向传播】构造BP网络--使用反向传播拟合线性模型
# y = wx模型
# 可视化:看训练多少轮,权重收敛情况
import torch
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w_data = []
epoch_data = []
epoch = 1
# 创建Tensor节点
w = torch.Tensor([66.0])
# 设置计算梯度
w.requires_grad = True
for epoch in range(1, 101, 1):
k = 1
# 每次都能拿到一个梯度,直接全部都用
for x, y in zip(x_data, y_data):
# 构建图(求均方误差~)
l = (w * x - y) ** 2
# 反馈,更新grad(梯度)值
l.backward()
# 根据梯度下降法公式更新权重
w.data = w.data - 0.01 * w.grad.data
# print("epoch:", epoch)
print(k, "号样本", "梯度值w.grad.item:", w.grad.item())
print("权重 W:", w.data.item()) # 注意需要通过 .item()取值哈! 2023.2.15 08:42
w_data.append(w.data.item()) # 这里也可以w_data.append(w.data),plt也能识别出来Tensor里面的数值
epoch_data.append(epoch)
# epoch += 1
w.grad.data.zero_()
k += 1
print("以上,即", epoch, "轮.\n")
print(epoch_data)
print("len(epoch_data):", len(epoch_data)) # 显然为300。因为100轮,每轮 都是 这三个样本 做计算
print(w_data)
print("len(w_data):",len(w_data)) # 显然也为300。
plt.plot(epoch_data, w_data)
plt.xlabel("Epoch")
plt.ylabel("W")
plt.show()
结果如下:可以看到权重的收敛情况,

我们知道 训练集的w=2,那么 结果越接近2拟合效果越好,可以看出,拟合地还是很好的!
1.3.8 补充——针对1.3.6,可视化,看参数w1、w2、b收敛情况 y ^ = ω 1 x 2 + ω 2 x + b \widehat y=\omega_1 x^2 + \omega_2x + b y =ω1x2+ω2x+b
只不过,这里的数据,是更符合该 非线性模型的,比起 目录1.3.6中的,要更完美。训练集:w1 = 2, w2 = 3, b= 4。
# 昵 称:XieXu
# 时 间: 2023/2/15/0015 9:01
# 反向传播,梯度下降
# 拟合y = w1x^2 + w2x + b(训练集:w1 = 2, w2 = 3, b= 4)
# y = w1x^2 + w2x + b
# 正确值:w1 = 2, w2 = 3, b = 4
import torch
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rc("font", family='Microsoft YaHei') # 配合显示坐标纵轴的 汉字说明
x_data = [0.0, 1.0, 2.0, 3.0]
y_data = [4.0, 9.0, 18.0, 31.0]
w1_data = []
w2_data = []
b_data = []
epoch_data = []
epoch = 1
# 创建Tensor节点
w1 = torch.Tensor([10.0])
w2 = torch.Tensor([10.0])
b = torch.Tensor([10.0])
# 设置计算梯度
w1.requires_grad = True
w2.requires_grad = True
b.requires_grad = True
# 可以试着调整,如训练1000轮、2000轮、3000轮、5000轮等
for epoch in range(1, 501, 1):
k = 1
# 每次都能拿到一个梯度,直接全部都用
for x, y in zip(x_data, y_data):
# 构建图
l = ((w1 * (x ** 2) + w2 * x + b) - y) ** 2 # 其实就是利用反向传播来求这个式子在各个权重方向的偏导
# 反馈,更新grad(梯度)值
l.backward()
# 根据梯度下降法公式更新权重
w1.data = w1.data - 0.01 * w1.grad.data # 也可以尝试 调整学习率
w2.data = w2.data - 0.01 * w2.grad.data
b.data = b.data - 0.01 * b.grad.data
print("由",k, "号样本:")
# print("epoch:", epoch)
print("W1:", w1.data.item()) # 注意 通过.item()取出 权重 (即以标量的形式取出) 2023.2.15 10:02
print("W2:", w2.data.item())
print("b:", b.data.item(), "\n")
w1_data.append(w1.data.item()) # 这里也可以w_data.append(w.data),plt也能识别出来Tensor里面的"数值"
w2_data.append(w2.data.item())
b_data.append(b.data.item())
epoch_data.append(epoch)
# epoch += 1
w1.grad.data.zero_() # 将权重的 梯度 清零(每次只用当前的 梯度来进行 权重的更新) 2023.2.15 10:11
w2.grad.data.zero_()
b.grad.data.zero_()
k += 1
print("以上,即 第", epoch, "轮\n")
plt.plot(epoch_data, w1_data, "g", label="W1")
# plt.legend(["W1"])
plt.plot(epoch_data, w2_data, "r", label="W2")
# plt.legend(["W2"])
plt.plot(epoch_data, b_data, label="b")
plt.legend(["W1", "W2", "b"])
plt.xlabel("Epoch")
plt.ylabel("三个参数的收敛情况")
plt.show()
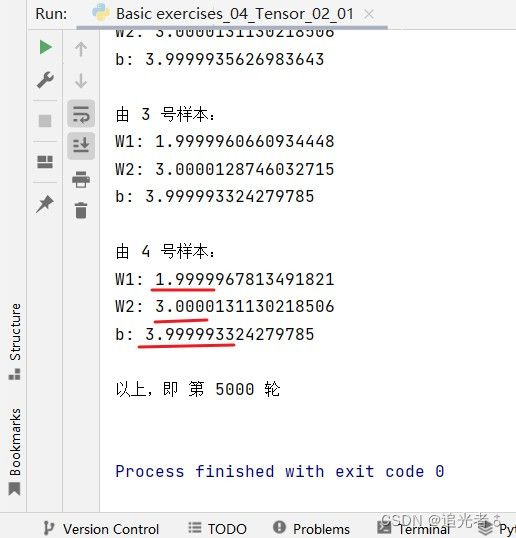
来看训练500轮的结果:
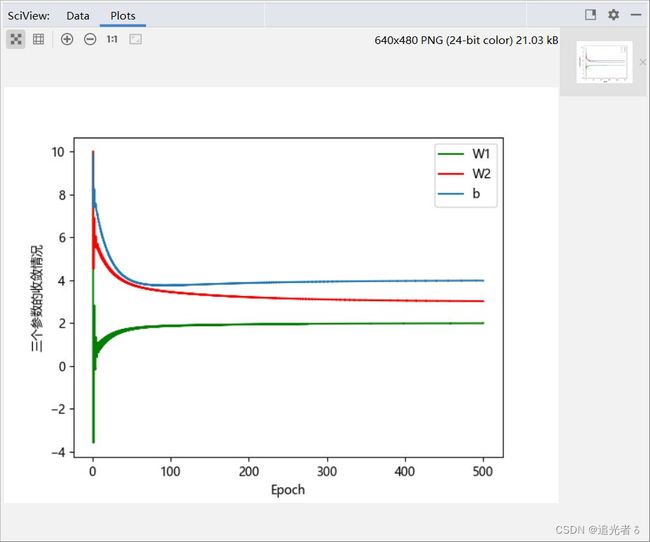
可以看出,w1、w2、b已经接近正确的值了(由上图 它们的收敛 也可以看出来):

训练1000轮:

是的,w1、w2、b的值已经更接近2、3、4了:

训练5000轮:

拟合的还是非常好的!各位也可以尝试调整学习率等 来看效果如何。
1.4 线性回归——使用PyTorch实现 y ^ = ω x + b \widehat y = \omega x +b y =ωx+b
1.4.1 Pytorch深度学习的一般流程
-
前馈(算损失)、反馈(算梯度)、更新(使用 (随机) 梯度下降算法 更新权重)!
-
前馈计算损失,反馈计算梯度!
用PyTorch进行深度学习模型构建的一般过程:
- [1] 准备数据集(Prepare dataset)
- [2]
设计用于计算最终结果的模型(Design model) - [3] 构造损失函数及优化器(Construct loss and optimizer)
- [4] 设计循环周期(Training cycle)——
前馈、反馈、更新
在pytorch中,若使用mini-batch的 (小批量随机梯度下降) 风格,一次性求出一个批量的 y ^ \widehat y y ,则需要 x x x以及 y ^ \widehat y y 作为矩阵参与计算【注:只要知道了 输入 x x x 和 输出 y ^ \widehat y y 各自的维度,那么 w w w和 b b b的维度就能推出来】,此时利用 numpy的广播机制,可以将原标量参数 ω \omega ω 扩写为 同维度的矩阵 [ w ] [w] [w],参与运算而不改变其Tensor的性质。
广播机制/扩充维度,以便可以实现矩阵相加~
![]()
w w w和 b b b 都会 自动扩充!例如 下所示:
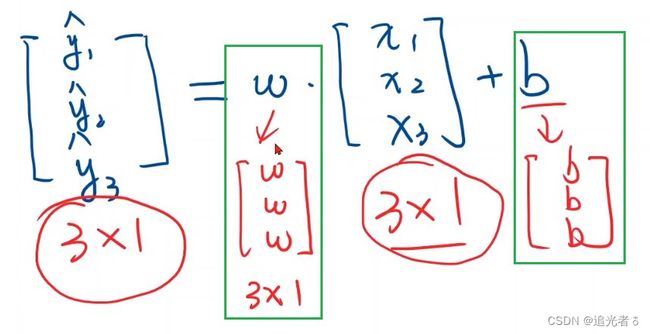
1.4.2 线性单元----Linear Unit
在下述 线性模型的计算图中,红框区域为线性单元,其中的 ω \omega ω以及 b b b是需要反复训练确定的,在设计时,需要事先设计出二者的维度。
(而由于公式 y ^ = ω x + b \widehat y = \omega x +b y =ωx+b,因此,只要确定了 y ^ \widehat y y 以及 x x x的维度,就可以确定上述两个量的维度大小)
例如:已知 x x x 和 z z z 或( y y y)的维度,即可求 w w w和 b b b的维度.
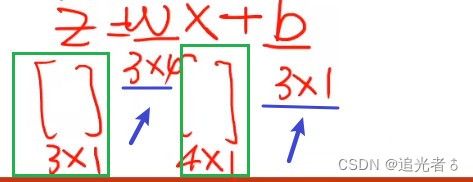
线性模型 “计算图”:

由上述理论,由于前边的计算过程都是针对矩阵的,因此最后的 l o s s loss loss也是矩阵,但由于 要进行 反向传播 调整参数,因此 l o s s loss loss应当是个标量,因此要对矩阵 [ l o s s ] [loss] [loss]内的每个量求和 并求 均值(MSE)。
l o s s = 1 N Σ [ l o s s 1 ⋮ l o s s n ] loss = \frac{1}{N}\Sigma \begin{bmatrix} {loss_1}\\ {\vdots}\\ {loss_n}\\ \end{bmatrix} loss=N1Σ loss1⋮lossn
1.4.3 练习(训练周期:前馈、反馈、权重更新)
使用PyTorch实现线性回归:
-
准备数据集
-
用类封装设计一个模型。目的是 为了前向传播forward,即计算 y ^ \widehat y y (预测值)
-
使用PyTorch的API 来定义 loss 和 optimizer。其中,计算loss是为了计算损失 从而反向传播 求解梯度,optimizer是为了根据得到的梯度 更新权重。
-
训练过程 :forward+backward+update (前馈 反馈 更新)
首先是几张图,便于理解:
无论哪种,目的都是把维度拼出来:

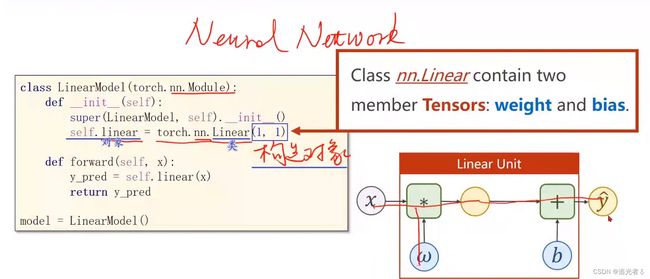
torch.nn.Linear 中的 部分参数 说明:

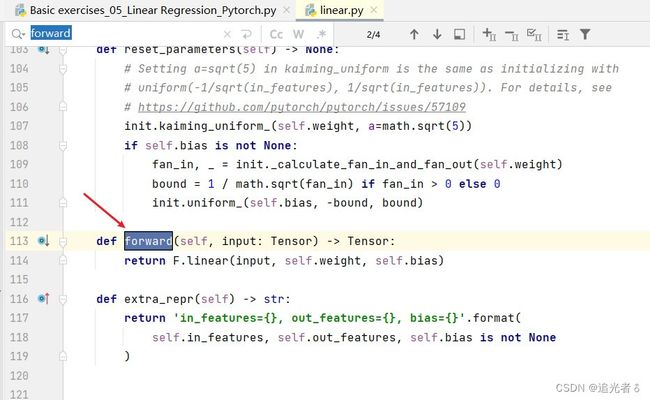
此外,为了便于理解下图中 forward()的参数,这里我已经做了说明。可回顾再往下的 Python基础语法知识~
注意:Python中,一个类实例要变成一个可调用对象,只需要实现一个特殊方法__ call __(),Module实现了函数 __ call __(),call()里面有一条语句是要调用forward()。因此新写的类中需要重写forward()覆盖掉父类中的forward()。
call()函数的作用是可以直接在对象后面加(),例如实例化的model对象 model = LinearModel(),和实例化的linear对象 self.linear = torch.nn.Linear(1, 1),y_pred = self.linear(x)。(这在下面的最终代码中 都将会看到)
self.linear(x)也由于函数call的实现 将会调用torch.nn.Linear类中的forward,至此完成封装,也就是说forward最终是在torch.nn.Linear类中实现的,具体怎么实现,可以不用关心,大概就是完成y= wx + b操作。
Python基础语法知识回顾(函数中 多个参数的传递,*args,**kwargs):当调用函数时,可以传入 数目 正好的值:
def func(a, b, c, x, y):
pass
func(1, 2, 3, x=6, y=7)
也可以传入 多个数量的值,这样即可实现:
def func(*args, x, y): # 定义 *args,那么用户就可以传入多个参数
print(args)
func(1, 2, 3, 9, x=6, y=7) # 用户传入 多个参数 1 2 3 9,然后再是x、y的匹配
输出:元组的形式,(进而可以取元素进行遍历)

上述内容中,x=6,y=7 也可 在函数中其他 形式来表示:
def func(*args, **kwargs): # 定义 *args,那么用户就可以传入多个参数,以元组的形式
print(args)
print(kwargs) # 两个star,那么 就会把参数变成 字典的形式
func(1, 2, 3, 9, x=6, y=7) # 用户传入 多个参数 1 2 3 9,然后再是x、y的匹配
输出:
![]()
以上操作,是函数里面,参数传递 常用到方式~
那么,
class Foobar:
def __init__(self):
pass
# 让对象可调用!!
def __call__(self, *args, **kwargs):
print("Hello" + str(args[0]))
foobar = Foobar()
foobar(1, 2, 3)
老师讲到,backward之前,要把梯度清零,这是框架里面的需求,老师特意强调的(在之前 自己 手动实现的 梯度下降---->反向传播 目录 1.3内的code,是 在 反向传播之后 才把梯度清零的…)en…总之,这里记得 在框架里面的话,backward 和 梯度下降 更新权重之前,先梯度清零!
基础上面所有这些分析,本次关于 【线性回归——PyTorch实现】的练习code如下,注释我写的也比较细:
# 昵 称:XieXu
# 时 间: 2023/2/15/0015 19:10
# 2023.2.16 08:53
import torch
# 1、准备数据集
# 数据作为矩阵参与Tensor计算
# x,y都是矩阵,(3行1列),即:共三个数据,每个数据 只有一个特征
x_data = torch.Tensor([[1.0], [2.0], [3.0]]) # 注意 x 和 y的值 都必须是“矩阵”
y_data = torch.Tensor([[2.0], [4.0], [6.0]])
# 2、使用类来 设计模型
''' 2023.2.16 08:41
我们的模型类应该继承于 nn.Module,它是所有神经网络模块的基类。
必须实现成员方法 __init__() 和 forward()
nn.linear类包含两个成员Tensors:weight和bias。
nn.linear类已经实现了神奇的方法__call__(),这使得该类的实例可以像函数一样被调用。
通常情况下,forward()将被调用。
'''
# 将我们的模型 定义为 类!! 2023.2.15 20:18
# LinearModel类 继承于 Module类 (Module这个父类 中有许多方法,是未来 模型训练过程中 要用到的!!)
class LinearModel(torch.nn.Module):
# 定义“构造函数”
# 即初始化 对象的时候 默认调用的函数
def __init__(self):
# 调用父类的init。【这就像是模板一样,写上就行!必须写!】
super(LinearModel, self).__init__() # 调用父类的initial
# Linear 是一个 类,torch.nn.Linear() 加括号 就是在“构建对象”! 2023.2.15 20:28
# Linear()这个 对象 包含 权重 weight(w)以及 偏置bias(b) 两个Tensor。。因此可以直接用linear 来完成 权重乘以输入 加上 偏置 的计算
# (1,1)是指输入x和输出y的特征维度,这里数据集中的x和y的特征 都是1维的 2023.2.16 08:44
# 该线性程 需要学习的参数 是w和b,获取w和b的方式分别是 linear.weight 和 linear.bias
self.linear = torch.nn.Linear(1, 1)
# 注:Linear 也是继承 自Module的,所以可以自动地进行 反向传播 ~ 2023.2.15 20:31
# self.linear 是个对象,这个对象的类型 是torch下 nn这个模块 中的 Linear这个类 ~ 2023.2.15 20:33
# nn为缩写,即 Neural Network 神经网络。(神经网络中的一个组件:Linear 它能够完成 权重和x相乘 算出中间值如Z Z再加上偏移量B 作为输出)
# 前馈函数forward,对父类函数 overwrite(重写、覆盖)2023.2.16 08:46
# 就得叫做 forward,一定要叫 这个名!!这是必须要定义的 2023.2.15 20:19
# 前馈的过程中 所要实现的计算~
def forward(self, x):
# 调用linear中的call(),以利用父类forward()计算wx+b
y_pred = self.linear(x)
return y_pred
# 之所以 这里没有 反馈函数backward,是因为 由Module构建的对象 会自动根据“计算图”生成
model = LinearModel() # 实例化模型
# 3、定义loss和优化器
# 构造的criterion对象所接受的参数为(y',y)
# criterion = torch.nn.MSELoss(size_average=False) # UserWarning: size_average and reduce args will be deprecated, please use reduction='sum' instead. warnings.warn(warning.format(ret))
criterion = torch.nn.MSELoss(reduction='sum') # 由上面警告,改为这样 即可~ 2023.2.15 23:13
# model.parameters()用于检查模型中所能进行优化的张量。即 model.parameters() 自动完成参数的初始化操作
# learningrate(lr)表学习率,可以统一 也可以不统一
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
# 4、训练周期:前馈、反馈、更新
for epoch in range(1000):
# 前馈计算y_pred
y_pred = model(x_data)
# 前馈计算损失loss
loss = criterion(y_pred, y_data)
# 打印调用loss时,会自动调用内部__str__()函数,避免产生计算图
# print(epoch, loss)
print(epoch, loss.item()) # 还是得以item来访问,输出loss的 取值 2023.2.16 09:01
# 梯度清零
optimizer.zero_grad() # 也有朋友把这称作“初始化梯度”...
# 梯度反向传播,计算图清除
loss.backward() # 自动反向传播,计算梯度值
# 根据传播的梯度以及学习率更新参数
optimizer.step() # 更新参数w和b 2023.2.16 08:51
# Output 输出最终的w和b
print('w = ', model.linear.weight.item())
print('b = ', model.linear.bias.item())
# TestModel 测试部分
x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print('y_pred = ', y_test.data)
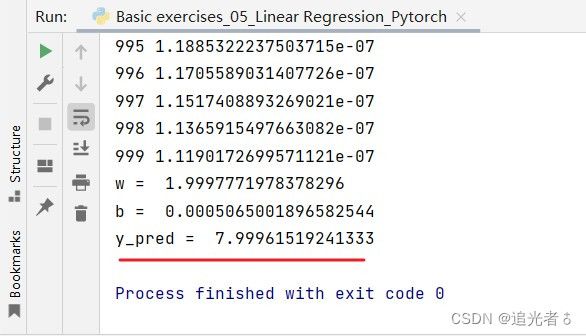
输出:
print('y_pred = ', y_test.item())
附:在翻看评论时发现的,便于理解吧~ (2023.2.17 23:24)
1.4.4 练习2——测试一下其它优化器效果如何
另外,可尝试 不同的优化器 在如上 的线性模型中的效果:

所用的code依然是基于上面小目录1.4.3,只是稍微改动一下,顺便加个可视化。(这里由于在调用LBFGS优化器 有些问题,因此这里就不测试了…故LBFGS相关注释可不用打开!!)
# 昵 称:XieXu
# 时 间: 2023/2/16/0016 9:57
# 验证不同优化器的效果
import torch
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rc("font", family='Microsoft YaHei') # 坐标系中汉字说明
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[2.0], [4.0], [6.0]])
epoch_list = []
Loss_list = []
class LinearModel(torch.nn.Module):
def __init__(self): # 构造函数
super(LinearModel, self).__init__()
self.linear = torch.nn.Linear(1, 1) # 构造对象,并说明输入输出的维数,第三个参数默认为true,表示用到b
def forward(self, x):
y_pred = self.linear(x) # 可调用对象,计算y=wx+b
return y_pred
model = LinearModel() # 实例化模型
criterion = torch.nn.MSELoss(reduction='sum')
# model.parameters()会扫描module中的所有成员,如果成员中有相应权重,那么都会将结果加到要训练的参数集合上
optimizer = torch.optim.SGD(model.parameters(), lr=0.01) # lr为学习率
# optimizer = torch.optim.Adagrad(model.parameters(), lr=0.01)
# optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
# optimizer = torch.optim.Adamax(model.parameters(), lr=0.01)
# optimizer = torch.optim.ASGD(model.parameters(), lr=0.01)
# optimizer = torch.optim.LBFGS(model.parameters(), lr=0.01) # TypeError: step() missing 1 required positional argument: 'closure'
# optimizer = torch.optim.RMSprop(model.parameters(), lr=0.01)
# optimizer = torch.optim.Rprop(model.parameters(), lr=0.01)
# def closure(): # 这里写的有问题,所以 暂时不测试 LBFGS优化器了!!
# y_pred = model(x_data)
# loss = criterion(y_pred, y_data)
# loss.backward()
# return loss
# optimizer.step(closure=closure)
for epoch in range(1000):
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
print(epoch, loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step() # 使用LBFGS优化器时会报错:TypeError: step() missing 1 required positional argument: 'closure'
# optimizer.step(closure=closure) # LBFGS优化器时报错,暂时不测试该优化器了...
# optimizer.zero_grad() # 梯度清零放到这里也行。。2023.2.16 16:08
epoch_list.append(epoch)
Loss_list.append(loss.item())
print('w=', model.linear.weight.item())
print('b=', model.linear.bias.item())
x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print('y_pred = ', y_test.data)
# print('y_pred = ', y_test.item())
plt.plot(epoch_list,Loss_list)
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.title("所用优化器:SGD")
# plt.title("所用优化器:Adagrad")
# plt.title("所用优化器:Adam")
# plt.title("所用优化器:Adamax")
# plt.title("所用优化器:ASGD")
# plt.title("所用优化器:LBFGS") # TypeError: step() missing 1 required positional argument: 'closure'...LBFGS优化器时报错,暂时不测试该优化器了..
# plt.title("所用优化器:RMSprop")
# plt.title("所用优化器:Rprop")
plt.show()
为了便于查看,我将轮数设置为100轮,上面的1000后面可自行修改~
此外,为了关于观察,我将所有图形都分别截取,然后放到如下一张图里面了。大家在实验时可以 自行打开注释,分别测试几个优化器即可~
可以看出,Adagrad优化器的损失是比较大的,其它几个优化器也各有千秋,有损失收敛比较快的,也由曲线形式收敛的~本例中,老师最初选取的是SGD–小批量随机梯度下降 优化器。
附:torch.nn.Linear的pytorch官方文档,可以看看官方的描述,进去后 甚至可以按照torch的版本 来选文档来看。
1.5 逻辑回归 (LogisticRegression)——基于PyTorch实现
1.5.1 问题背景——二分类问题
注:截止到上面的所有实例,使用的 都是 学习时间----对应得分的例子,即 学习1小时 得2分,学习2小时 得4分,学习三小时 得6分…这是问题背景。
本目录,记录逻辑回归,众所周知,它是解决分类问题的,虽然名字里边带回归…常用的损失函数 是交叉熵损失函数~
针对上面学习时间----得分的示例,这里 的问题背景是:学习时间----是否及格,即学习1小时----不及格(记为类别0),学习2小时----不及格(类别0),学习三小时----及格(记为类别1),判断:学习4小时,是否及格呢?
显然,这是 二分类问题。
1.5.2 常做练习用的数据集介绍:MNIST 和 CIFAR-10
[1] 手写数字数据集:
即 MNIST数据集。
该数据集的基础内容是:
[2] CIFAR-10数据集(十种 事物/物体 的数据集):
基础内容是:
- 训练集 Training_set: 共 50000 个样本;
- 测试集 Test_set: 共 10000个样本;
- 物品个数 Classes: 10 种类别,分别是:飞机、汽车、鸟、猫、鹿、狗、青蛙、马、船、卡车 这十种物品/事物。

1.5.3 二分类 与 sigmoid
我们知道,二分类,要么可以标记为0,要么标记为1,非此即彼。我们得到的结果 是 输入数据 所属的类别。这与之前的回归问题(结果的取值是连续的) 有所不同,分类问题中,得到的结果 一般是 不连续的,即离散的。
在二分类问题中,我们怎样衡量 输入数据 运算过后 所属的类别?
一般是通过概率来表示,这也是容易理解的,有输入数据,经过运算,我们得到 它对应于 这些类别的各个概率值,哪个概率值大,就认定为 它是 属于 哪个类别。
所有类别的概率之和 =1 ,在二分类中,那么就有:
P ( y ^ = 1 ) + P ( y ^ = 0 ) = 1 P(\widehat y=1)+P(\widehat y=0) = 1 P(y =1)+P(y =0)=1
由于非此即彼,那么 只需要计算一种类别的结果,就自然而然知道 属于另一种类别的概率了。这里,一般计算 P ( y ^ = 1 ) P(\widehat y=1) P(y =1)。
紧接着考虑到的问题是,概率的取值 一定是0到1的 即 y ^ ∈ [ 0 , 1 ] \widehat y \in [0,1] y ∈[0,1],因此,就需要对之前模型 y ^ = ω x + b \widehat y = \omega x+b y =ωx+b 得到的结果进行一个映射,把它的值 映射到 0到1之间,这里用到的映射函数是,sigmoid函数(也常称为 逻辑函数),也是极其常见的一个函数。该函数的特性如下:
σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1+e^{-x}} σ(x)=1+e−x1
由下面其图像可知:
- 函数值在0到1之间变化明显(曲线陡 函数值激增,导数大)
- 在趋近于0和1处函数逐渐平滑(导数小)
- 函数为饱和函数(x超过某值时,导数变得越小,sigmoid曲线逐渐平缓,大致是这种意思;)【满足 lim x → + ∞ f ′ ( x ) → 0 \lim \limits_{x\rightarrow+\infty}f'(x)\;\rightarrow0 x→+∞limf′(x)→0 的函数为右饱和函数;满足 lim x → − ∞ f ′ ( x ) → 0 \lim \limits_{x\rightarrow-\infty}f'(x)\;\rightarrow0 x→−∞limf′(x)→0的函数为左饱和函数。同时满足二者的为饱和函数】
- sigmoid函数 为单调增函数
- 由其公式 和 数学知识 容易知道,x取0时 sigmoid(0)=0.5,x取正无穷时 sigmoid(正无穷) 无限趋近1,x取负无穷时 sigmoid(负无穷) 无限趋近0。
这个函数 原名为 logistics函数,属于sigmod类函数,由于其特性优异,代码中的sigmod函数就指的是该函数,这也是约定俗成的!其函数图像为:
sigmoid函数图像:

另外,其导函数大致如此:有些像 正态分布的曲线…
![]()
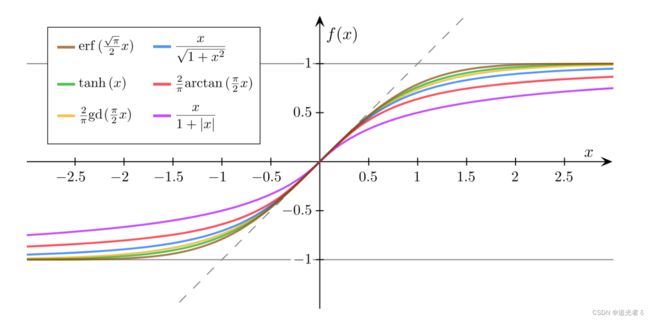
注:此外,还要其它形式的sigmoid函数:
1.5.4 模型的变化:由线性回归模型---->二分类模型,增添sigmoid函数;损失函数的变化:由线性回归损失函数(MSE 均方误差损失函数) ---->二分类损失函数BCELoss (mini-batch 小批量交叉熵损失函数cross entropy)
经过上面的分析,容易知道,sigmoid函数的输入值 即 参数 为 y ^ \widehat y y 。(输出值 套上了 一个sigmoid函数,仅此而已,其它都是差不多的。再就是数据中 输出值 为0或1(分类结果) )
原来的线性回归模型 变为了 二分类模型:
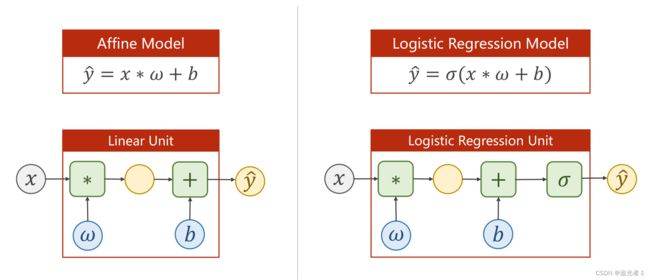
损失函数Loss的变化:
之前,我们是计算两个标量 数值间的差距,也就是数轴上的距离。
现在,为了计算(表示) 两个概率之间的差异(可以用 “分布”这个词来形容一下),需要利用到交叉熵的理论。
看上图中带 l o g log log的那个公式,若 y = 0 y=0 y=0,则取括号中 加号后边的那个式子,即 l o s s = − l o g ( 1 − y ^ ) loss=-log(1-\widehat y) loss=−log(1−y ),老师讲到,这是在计算分布的差异,如概率论与数理统计中 KL散度(这个知识我了解不够,需要补)、cross-entropy 即交叉熵损失函数。继续看公式,我们希望 l o s s loss loss尽可能小,而公式中带了负号,那么 即 希望 l o g ( 1 − y ^ ) log(1-\widehat y) log(1−y )尽可能大,而 l o g log log函数是单调增函数,则希望 1 − y ^ 1-\widehat y 1−y 尽可能大,即 希望 y ^ \widehat y y 尽可能小,即 y ^ \widehat y y 越 无限趋近0 越好。反之,输出的 y = 1 y=1 y=1时,同样的道理,为了 l o s s loss loss尽可能小,我们希望 y ^ \widehat y y 尽可能接近1。
例如下边,有两个分布,可用如下绿框中的形式 来表示这两个分布之间 差异性的大小:我们希望 这个值 越大越好!

目标是,在训练的时候,让分布尽可能地去接近 真实类别。本例中,使用的是 小批量 的二分类损失函数(BCE Loss):可以看到,类别为1时, y ^ \widehat y y 值越接近1,BCE损失函数越小,反之越大;同理,类别为0时, y ^ \widehat y y 值越接近0,BCE损失函数越小,反之BCE损失函数越大。
(注:BCELoss 是CrossEntropyLoss的一个特例,只用于二分类问题,而CrossEntropyLoss可以用于二分类,也可以用于多分类。如果是二分类问题,建议用BCELoss)
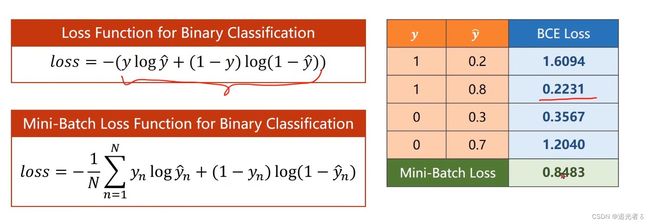
再次 附:关于 torch.nn.BCELoss官方文档
1.5.5 code练习
问题背景,即上面提到的。
# 昵 称:XieXu
# 时 间: 2023/2/16/0016 17:51
import torch.nn.functional as F
import torch
# 【1】Prepare data
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[0.0], [0.0], [1.0]]) # 这里与之前不同,分别是0/1两种类别,不合格/合格 2023.2.16 17:53
# 【2】Design model
# 改用LogisticRegressionModel 也是同样继承于Module
class LogisticRegressionModel(torch.nn.Module):
def __init__(self):
super(LogisticRegressionModel, self).__init__()
self.linear = torch.nn.Linear(1, 1)
def forward(self, x):
# 对原先的linear结果进行sigmod激活,将y_hat值 映射到0~1之间
# y_pred = F.sigmoid(self.linear(x)) # UserWarning: nn.functional.sigmoid is deprecated. Use torch.sigmoid instead.
y_pred = torch.sigmoid(self.linear(x)) # 2023.2.16 20:05
return y_pred
# 实例化 2023.2.16 17:53
model = LogisticRegressionModel()
# 【3】Select criterion and optimizer (using PyTorch API)
# 构造的criterion对象所接受的参数为(y_hat,y),这里的y_hat指的是归一化之后的(初始计算的y_hat 被映射到0~1之后的值)
# UserWarning: size_average and reduce args will be deprecated, please use reduction='sum' instead.
# 这个警告~ 和之前线性模型也遇到的一样,
# criterion = torch.nn.BCELoss(size_average=False) # 计算损失
criterion = torch.nn.BCELoss(reduction='sum') # 计算损失 【默认对一个batch里面的数据做二元交叉熵并且求平均。】
optimizer = torch.optim.SGD(model.parameters(), lr=0.01) # 梯度下降更新权重
# 【4】Training cycle 10000轮时,效果近乎100%
for epoch in range(1000):
y_pred = model(x_data) # 输入参数,得到 被映射到 0~1 之间的 (新的)y_hat值
loss = criterion(y_pred, y_data) # 利用BCELoss损失函数 计算损失值
print(epoch, loss.item())
optimizer.zero_grad() # 梯度清零。2023.2.16
loss.backward() # 反向传播,求解梯度
optimizer.step() # 梯度下降 更新权重
print('w = ', model.linear.weight.item()) # 注意通过item()来访问 取值 2023.2.16 17:54
print('b = ', model.linear.bias.item())
x_test = torch.Tensor([[4.0]]) # 测试。看 当x=4时,
y_test = model(x_test) # 即问题背景下的 学习时间为4小时 时,合格/不合格 两种类别
print('y_pred = ', y_test.data) # 得到最终的概率值... 概率大,指的是取值为1,即合格。反之,概率值小,意为不合格。
# print('y_pred = ', y_test.item()) # 和上一行,哪个 都可~
# print(type(y_test)) # 
若训练10000轮:可以看到结果如下,这说明,输入:学习时间为4小时 时,结果为合格的概率近乎100%,即确定合格。(若不想看到tensor,只想看到y_pred的数值,可以 直接把最后输出y_pred的语句改为 print('y_pred = ', y_test.item()) 即可,因为y_pred的类型也是一个Tensor)
1.6 处理多维特征的输入
1.6.1 问题背景,含 多维特征 的数据集
在上面的介绍中,x大都只有一个特征,即只有一个维度,那么 当x的维度是多维时,即 输入有多个特征时,如何处理?
之前的数据集:

本次使用的 含多维特征的数据集——糖尿病数据集(sklearn中 其实也有类似的糖尿病数据集):每个样本/记录(sample/record)有8个维度的信息(feature),并以此进行二分类。Y表示一年后 糖尿病 病情是否加重。
1.6.2 多维度特征的处理;Mini-batch;多层神经网络
在之前,单个特征维度 的 逻辑回归模型为:
y ^ ( i ) = σ ( x ( i ) ω + b ) \widehat y^{(i)} = \sigma(x^{(i)} \omega+b) y (i)=σ(x(i)ω+b)
其中的 x ( i ) x^{(i)} x(i)表示第i个样本的维度,对于多维度,输入要变为8个维度的输入,因此,模型应当变为:
y ^ ( i ) = σ ( ∑ n = 1 8 x n ( i ) ω n + b ) \widehat y^{(i)} = \sigma(\sum _{n=1}^8 x^{(i)}_n \omega _n+b) y (i)=σ(n=1∑8xn(i)ωn+b)
其中的 x n ( i ) x^{(i)}_n xn(i)表示第i个样本的第n个维度。由于在实际代码运算中是以矩阵进行计算的,因此:
∑ n = 1 8 x n ( i ) ω n = [ x 1 ( i ) ⋯ x 8 ( i ) ] [ w 1 ⋮ w 8 ] \sum _{n=1}^8 x^{(i)}_n \omega _n = \begin{bmatrix} {x_1^{(i)}}&{\cdots}&{x_8^{(i)}} \end{bmatrix} \begin{bmatrix} {w_1}\\ {\vdots}\\ {w_8} \end{bmatrix} n=1∑8xn(i)ωn=[x1(i)⋯x8(i)] w1⋮w8
回到原式,故可以表示成:
y ^ ( i ) = σ ( [ x 1 ( i ) ⋯ x 8 ( i ) ] [ w 1 ⋮ w 8 ] + b ) = σ ( z ( i ) ) \widehat y^{(i)} = \sigma( \begin{bmatrix} {x_1^{(i)}}&{\cdots}&{x_8^{(i)}} \end{bmatrix} \begin{bmatrix} {w_1}\\ {\vdots}\\ {w_8} \end{bmatrix}+b)\\ =\sigma(z^{(i)}) y (i)=σ([x1(i)⋯x8(i)] w1⋮w8 +b)=σ(z(i))
(转换成矩阵运算,就可以更好地利用CPU/GPU的特性,来提高运行速度和效率等)
Mini-batch
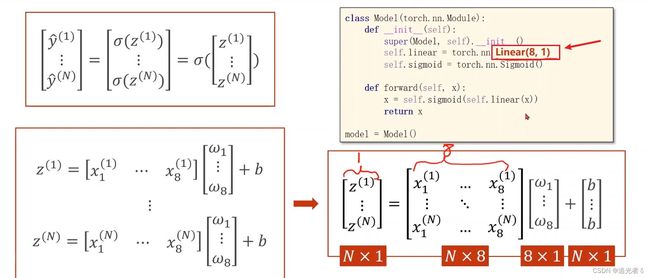
基于上面对数据的处理,我们就可以对小批量数据也 合并 成 矩阵运算:
[ y ^ ( 1 ) ⋮ y ^ ( N ) ] = [ σ ( z ( 1 ) ) ⋮ σ ( z ( N ) ) ] = σ ( [ z ( 1 ) ⋮ z ( N ) ] ) \begin{bmatrix} {\widehat y^{(1)}}\\ {\vdots}\\ {\widehat y^{(N)}} \end{bmatrix}= \begin{bmatrix} {\sigma(z^{(1)})}\\ {\vdots}\\ {\sigma(z^{(N)})} \end{bmatrix} =\sigma( \begin{bmatrix} {z^{(1)}}\\ {\vdots}\\ {z^{(N)}} \end{bmatrix}) y (1)⋮y (N) = σ(z(1))⋮σ(z(N)) =σ( z(1)⋮z(N) )
其中,
z ( i ) = [ x 1 ( i ) ⋯ x 8 ( i ) ] [ w 1 ⋮ w 8 ] + b z^{(i)}= \begin{bmatrix} {x_1^{(i)}}&{\cdots}&{x_8^{(i)}} \end{bmatrix} \begin{bmatrix} {w_1}\\ {\vdots}\\ {w_8} \end{bmatrix}+b\\ z(i)=[x1(i)⋯x8(i)] w1⋮w8 +b
从而有,
[ z ( 1 ) ⋮ z ( N ) ] = [ x 1 ( 1 ) ⋯ x 8 ( 1 ) ⋮ ⋮ ⋮ x 1 ( N ) ⋯ x 8 ( N ) ] [ w 1 ⋮ w 8 ] + [ b ⋮ b ] \begin{bmatrix} {z^{(1)}}\\ {\vdots}\\ {z^{(N)}} \end{bmatrix}= \begin{bmatrix} {x_1^{(1)}} & {\cdots} & {x_8^{(1)}}\\ {\vdots} & {\vdots} & {\vdots}\\ {x_1^{(N)}} & {\cdots} & {x_8^{(N)}}\\ \end{bmatrix} \begin{bmatrix} {w_1}\\ {\vdots}\\ {w_8} \end{bmatrix} + \begin{bmatrix} {b}\\ {\vdots}\\ {b} \end{bmatrix} z(1)⋮z(N) = x1(1)⋮x1(N)⋯⋮⋯x8(1)⋮x8(N) w1⋮w8 + b⋮b
整体上,将之前的标量运算,转换为矩阵运算,以方便进行并行计算,提高算法效率。下图指明了矩阵的维度, N X 8 N X 8 NX8矩阵中,每一行是 各个样本的第1到第8个特征; 8 X 1 8 X 1 8X1矩阵中,8行,每行一个权重,按照矩阵乘法,这两个矩阵分别相乘,即 每个样本的:每个特征 与 对应每个特征的权重相乘,每个样本 都有8个特征,特征与权重 乘完,再 各自 加上 偏置 b b b。

因此,对于模型的修改,即:输入维度改为8,输出维度仍为1即可。
X: N X 8 N X 8 NX8 维;
Y: N X 1 N X 1 NX1 即可~ 另外,偏置 b b b 可通过“广播机制”自动扩充。
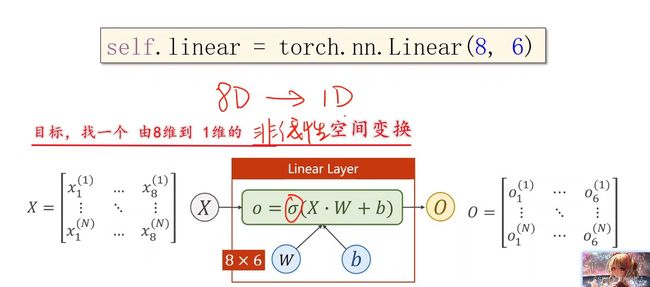
故,只需要将Linear()中的参数改成下面代码,即可完成 从8维输入到1位输出的过程。
self.linear = torch.nn.Linear(8,1)
多层神经网络
老师讲到:什么是矩阵?矩阵是一种空间变换的函数。
例,将 x x x由 N N N维空间 映射到 M M M维空间去:

例,把任意 8维空间的向量,映射到二维空间上(这里是 线性映射):
经常要做的空间变换,不一定是线性的,而是非常复杂的非线性的!我们用多个线性变换层,通过找到最优的权重,把它们组合起来,来模拟出 非线性变换。
那么,如果不用(8,2),而用(8,6),就可以把输入 x x x 从8维空间 降到 6维空间,后面 可以再从 6维 降到 2维,2维 降到 1维。把维度 分布地进行降低。
由此可以增加网络层数,增加网络复杂度。此外,对网络结构 先增后减,即先扩充维度 再降低维度,也是OK的。这里,Linear 能做到空间维度的变换。
分布降低,由于它是纯线性的,所以在把它们 接起来之前,要记得 σ \sigma σ!因为Linear是不做非线性的(通过 σ \sigma σ 将其转换为 非线性)。因此这几次的变换,每一次的 空间压缩 都引入 一个非线性,这样我们只要调整 每一步线性变换,我们就可以用 这样的方式 来 去拟合 我们真正想要的 空间变换。【老师原话】
在神经网络里面, σ \sigma σ叫做激活函数,通过引入 σ \sigma σ激活函数,给线性变换 增加 非线性(因子)。使得可以去拟合 相应地 非线性变换。【这就是神经网络 设计 所采用的方式】
变换的维度和层数,决定了网络的复杂程度。但是具体,取什么值比较好?这个是 超参数搜索的问题。一般来说,隐层越多,即中间执行的步骤越多,中间的神经元越多,那么 非线性变换的学习能力就越强!但是 但是 但是,学习能力越强并不是越好,这样会把输入样本里面 噪声的规律也学到。。噪声是我们不想要的,且这个噪声 和 真实的应用场景里面的噪声 不一定是一样的。我们要学的 是 数据真值本身的规律。 学习能力太强,并不好。即学习能力 必须要有 泛化能力 才是最好的。【老师讲到,要练习 读文档的能力;具有基本的架构的理解能力(CPU架构/GPU/操作系统/主机架构/内存管理/编译原理架构等) 】
1.6.3 练习
基于上述分析。
本次【问题背景:糖尿病–病情是否加重】练习用到的模型:

大致思路,同之前:
构造 损失函数和优化器:输出仍是概率,即 y ^ = 1 \widehat y=1 y =1的概率,故依然用BCE损失,

训练周期中,这里没有用到mini-batch,而是把所有数据都放进来了。(至于minibatch,后面 将会在pytorch所提供的工具类 DataLoader 记录)

(关于下述Model类,Python代码中的 一些关键词,构造函数、super函数、父类、 子类、方法(函数)重写/覆盖)
# 昵 称:XieXu
# 时 间: 2023/2/17/0017 9:15
# 处理多维特征的输入
import torch
import numpy as np
# 读取文件,一般GPU只支持32位浮点数
xy = np.loadtxt('diabetes.csv', delimiter=',', dtype=np.float32) # 也可以读取 .gz 压缩文件
# 确保x_data 和 y_data 在计算过程中 都得是矩阵!不能是一个向量 2023.2.17 11:15
# torch.from_numpy 会创建Tensor
# x_data = torch.from_numpy(xy[:-1, :-1]) #-1行-1列不取
x_data = torch.from_numpy(xy[:, :-1]) # 第一个:是指 读取所有行, 第二个:是指从第一列开始,最后一列不要。(即 取前8列)
# y_data = torch.from_numpy(xy[:-1, [-1]]) #单取-1列作为矩阵
y_data = torch.from_numpy(xy[:, [-1]]) # [-1] 最后得到的是个矩阵 (即 取最后一列)
'''
查看数据集的 分割
print(x_data.item()) # ValueError: only one element tensors can be converted to Python scalars
print(x_data)
print(x_data.shape) # torch.Size([759, 8]),只取前8列,即作为输入x 8个特征
print(y_data) # 数据集中的最后一列,以矩阵的形式~
print(y_data.shape) # torch.Size([759, 1])
'''
# 取-1行的测试集部分
test_data = torch.from_numpy(xy[[-1], :-1]) # 即最后一行的 x 输入数据
pred_test = torch.from_numpy(xy[[-1], [-1]]) # 最后一行 的 最后一列,即1(类别)
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self.linear1 = torch.nn.Linear(8, 6)
self.linear2 = torch.nn.Linear(6, 4)
self.linear3 = torch.nn.Linear(4, 1)
self.sigmoid = torch.nn.Sigmoid() # 这里 torch.nn.Sigmoid() 将其看做是网络的一层,而不是普通的函数使用
# self.ReLU = torch.nn.ReLU()
def forward(self, x):
x = self.sigmoid(self.linear1(x))
x = self.sigmoid(self.linear2(x))
x = self.sigmoid(self.linear3(x))
# x = self.ReLU(self.linear1(x))
# x = self.ReLU(self.linear2(x))
# x = self.sigmoid(self.linear3(x))
return x
# 实例化 2023.2.17 09:17
model = Model()
# 二分类 交叉熵损失函数
# criterion = torch.nn.BCELoss(size_average=True) # UserWarning: size_average and reduce args will be deprecated, please use reduction='mean' instead.
criterion = torch.nn.BCELoss(reduction='mean') # 2023.2.17 11:09
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
# 1000轮数时 test_pred 为0.65左右,
# 10000轮时,test_pred 为0.94左右。迭代次数增多,训练效果更好了~
for epoch in range(10000):
# Forward 这里并非mini-batch的设计(把所有数据都扔进来了),只是mini-batch的风格
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
print(epoch, loss.item())
# Backward
optimizer.zero_grad()
loss.backward() # 反向传播,
# Update
optimizer.step() # 更新 权重
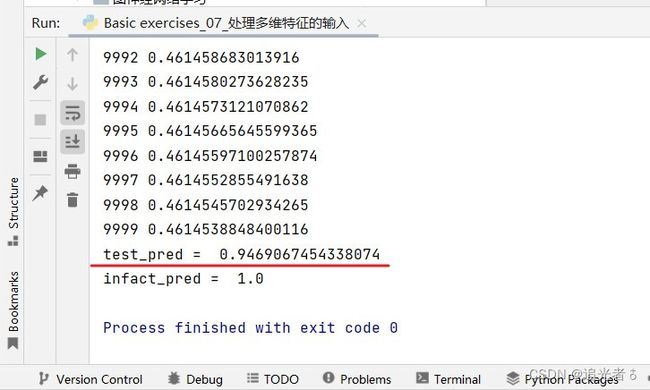
print("test_pred = ", model(test_data).item())
print("infact_pred = ", pred_test.item())
训练10000轮:可以看到,与真实值1.0已经比较接近了!
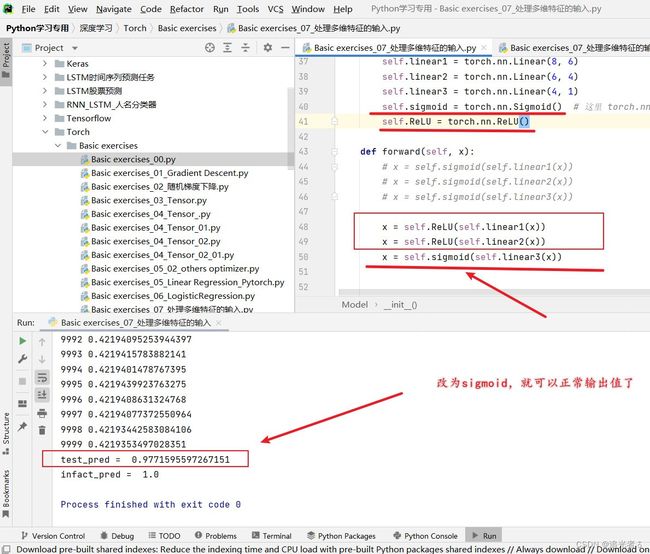
在使用其他激活函数时,记得forward()方法中的最后部分 要写sigmoid哈!否则就 容易会:
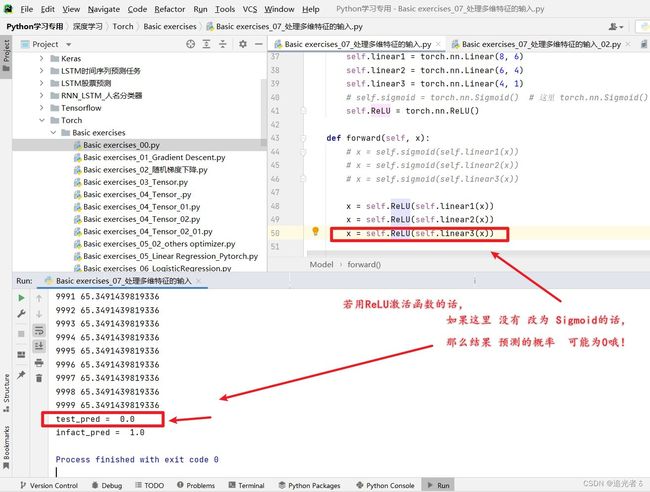
嗯…用了ReLU激活函数,要比原来 概率还要高呢:
1.6.4 可视化,使用 Adam优化器/SGD优化器 试试看
这里我只训练了30万轮。是需要一些时间的。使用的是默认的CPU,没用GPU运行。
# 昵 称:XieXu
# 时 间: 2023/2/17/0017 13:40
import numpy as np
import torch
import matplotlib.pyplot as plt
# prepare dataset
xy = np.loadtxt('diabetes.csv', delimiter=',', dtype=np.float32)
x_data = torch.from_numpy(xy[:, :-1])
y_data = torch.from_numpy(xy[:, [-1]])
# design model using class
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self.linear1 = torch.nn.Linear(8, 6) # 输入数据x的特征是8维,x有8个特征,输出为6维
self.linear2 = torch.nn.Linear(6, 4)
self.linear3 = torch.nn.Linear(4, 1)
self.sigmoid = torch.nn.Sigmoid() # 将其看作是网络的一层,而不是简单的函数使用
def forward(self, x): # 构建一个计算图
x = self.sigmoid(self.linear1(x))
x = self.sigmoid(self.linear2(x)) # 将上面一行的输出作为输入
x = self.sigmoid(self.linear3(x))
return x
model = Model() # 实例化
# construct loss and optimizer
# model.parameters()会扫描module中的所有成员,如果成员中有相应权重,那么都会将结果加到要训练的参数集合上
criterion = torch.nn.BCELoss(reduction='mean')
# optimizer = torch.optim.SGD(model.parameters(), lr=0.1) # 30w次,效果acc=0.84 loss=0.37
optimizer = torch.optim.Adam(model.parameters(), lr=0.1) # 20w次,效果acc=0.85 2023.2.17 14:33
epoch_list = []
loss_list = []
# training cycle forward, backward, update
for epoch in range(1,300001,1):
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
# print(epoch, loss.item())
epoch_list.append(epoch)
# loss_list.append(loss)
loss_list.append(loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 输出准确率acc为评价指标
if epoch % 10000 == 0:
# 预测的概率大于0.5的话,这里就认为 预测类别属于1,否则就属于0(二分类~)
# torch.where(condition,a,b)其中,输入参数condition:条件限制,如果满足条件,则选择a,否则选择b作为输出。
y_pred_label = torch.where(y_pred >= 0.5, torch.tensor([1.0]), torch.tensor([0.0]))
# 计算正确的数量
acc = torch.eq(y_pred_label, y_data).sum().item() / y_data.size(0) # 即 预测值 要么1正确/要么0不正确 二分类!!!2023.2.17 16:35
print("epoch = ", epoch, "loss = ", loss.item(), "acc = ", acc)
# 可视化
plt.plot(epoch_list, loss_list)
plt.ylabel('Loss')
plt.xlabel('Epoch')
# plt.title("Loss with epoch (SGD)")
plt.title("Loss with epoch (Adam)")
plt.show()
至于,
训练30w次,使用SGD(随机梯度下降)优化器的效果:acc=0.84 loss=0.37
训练30w次,使用Adam优化器的效果:acc=0.83 loss=1.38。反而不如SGD了。这有可能过拟合了。

我又测试了下Adam优化器,训练了1w轮:acc为0.87,要比上边30w轮效果还好…

同样是1w轮,SGD优化器效果 acc=0.76,这时候不如Adam优化器效果好。
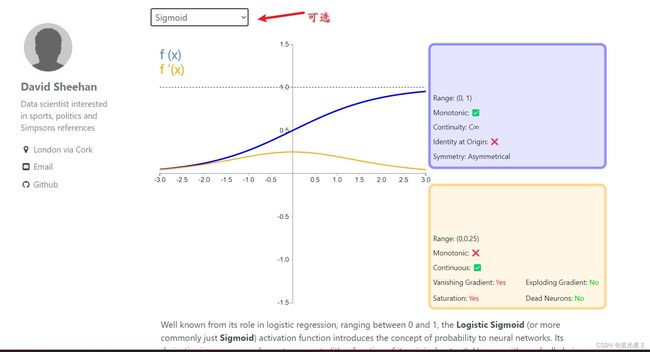
1.6.5 附:可尝试 不同的激活函数

可以看到激活函数的图像(蓝色) 以及 其导函数的图像(浅黄色),ReLU激活函数:

Tanh激活函数:
另外,PyTorch中提供了 大量的激活函数:PyTorch激活函数 官方文档
修改如下地方,可测试不同的激活单元(函数) 对神经网络性能的影响,如下边使用的是ReLU激活函数:【注意若要求概率的话,最后一层要使用sigmoid激活函数】

其实已经在上面目录1.6.3使用过 ReLU激活函数了。关于其它激活函数,读者可自行替换 尝试实验 即可。【要记得forward的最后部分 依然使用sigmoid哈!否则 可能会出现概率值为0的情况!(概率 为0~1)】
不同的激活函数(降低维度用/映射用/)、不同的优化器(梯度下降or求偏导用)、不同的学习率、不同的训练轮数等。有很多值得调试的超参数哈哈哈!
1.7 加载数据集 Dataset and DataLoader
1.7.1 Dataset类、DataLoader类;Epoch、Mini-batch、Iteration;
DataSet 和 DataLoader,是用于加载数据的工具类。
-
DataSet 用于构造数据集,数据集 应该支持
索引/下标操作;DataSet 是一个抽象类(只能通过继承实现) -
DataLoader是用于拿出
Mini-Batch,即一组数据,用于训练,来快速使用。
在进行梯度下降的时候,我们传入数据时,可以选择随机梯度下降,每次只用一个样本,这样会得到比较好的随机性,也会帮助我们跨越 将来在优化过程中 所遇到的“鞍点”。训练出的模型 性能会比较好。但是会导致在优化的时候 用的时间过长。(每次一个样本,这无法利用CPU或GPU的并行能力,所以训练的时间 是会非常长的)
// 若一次性 把所有数据都 执行梯度下降,即Batch,它的优势是 可以最大化利用 向量计算的优势,来提升计算的速度。虽然计算速度非常快,但是在求得的模型性能上,可能不是那么好。
因此,在深度学习中,会使用Mini-batch的方法,来均衡 在性能 和 训练时间上的平衡需求。
Epoch,Batch-Size,Iteration
在外层循环中,每一层是一个epoch(训练周期),在内层循环中,每一次是一个Mini-Batch(Batch的迭代).

epoch、batch-size、Iteration的概念亦如下图所解释:
1.7.2 DataLoader类 核心参数解释
batch_size:每次训练的时候所使用的样本数量,一般指定2的幂次数shuffle:(可理解为“洗牌”,用于打乱顺序,提高训练的随机性),这样每一次生成的batch_size中的数据集,都是具有随机性的,
通过获得DataSet(数据集)的索引(即 可用下标访问) 以及 数据集大小(len),来自动地生成小批量训练集。
具体地,DataLoader先对数据集进行洗牌【打乱】,再将数据集按照Batch_Size的长度划分为小的Batch【分组】,并按照Iterations进行加载,以方便 通过循环对每个Batch进行操作。
1.7.3 如何在代码层面实现 Dataset和DataLoader
这里,老师讲到:在构造数据集时,在__init()方法里,两种对数据加载到内存中的处理方式如下:
- [1]
加载所有数据到dataset,每次使用时 读索引,这适用于数据量小的情况。(如本例中,糖尿病的数据集,就是一个关系表,很小,直接从内存中读取就好。但是如果是 图像数据集,几十G,那么 在initial里把数据都读进来,这显然是不可能的!通常,把它们打包到一个文件里面) - [2] 只对dataset 进行初始化,
仅存 文件名 到列表,每次使用时 再通过索引到内存中去读取。
num_workers 指的是 对于Mini-batch内的数据集,读的时候,是否要用 多线程。即:到底 用几个并行的进程 去读取数据。并行 可以 提高 读取的效率(在windows下,若遇到num_workers参数设置会报错的,用if__main__包起来就OK了,亦或是将num_workers设置为0)

使用Loader时可能会遇到问题:(这是由于torch0.4的版本所致)

只需要将迭代的语句 封装到 if语句里面,或者函数里面,就可以解决该报错:
进一步,数据集的类 是如何实现的:

training cycle的变化:变成了二重循环,外层即Epoch,
Dataset每次拿过来的 都是X的第i行,和 Y的第i行,DataLoader每次根据Mini-batch的数量,会把X和Y 各自变为矩阵,且会自动地转换成Tensor,因此这里直接data即可,不用再 自己手动转换为Tensor了。
简言之,与之前的区别就是,把data中的数据 解成 X X X和 Y Y Y。

当然,也有另外一种写法,可以不写 inputs,labels = data,
即,直接 写在上面,这种形式:for i,(inputs,labels) enumerate(train_loader,0),本意都是一样的。
整体步骤:
![]()
1.7.4 其它说明:torchvision内置数据集
torchvision中内置了很多数据集,可以直接去使用,这些数据集都是派生自Dataset,因此有__getitem__和__len__等方法的实现,当然 这些数据集 也可以用 DataLoader来进行加载。并且可以使用多进程 来进行加速。

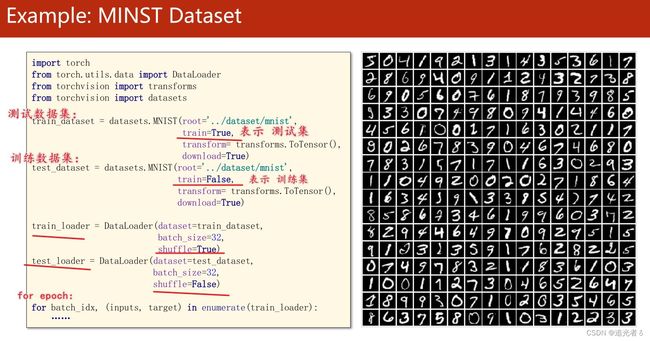
如之前提到过的手写数字数据集:MNIST(入门图像识别,常会用到的),要使用该数据集,只需要从torchvision将datasets导入进来即可。datasets中 有一个MNIST类,可用该类 来构造一个MNIST实例。
参数:路径、训练集/测试集、图像要做什么样的transform(变换 )【即 PIL Image 类型 —>>Tensor张量 。图像中的像素值 为0~255,将其缩放到0 ~ 1或者-1 ~ +1等区间的操作】、download(若没有该数据集,是否联网下载)
在训练数据集中,通常把shuffle设置为true。在测试的时候,因为对模型是没有改变的,所以把shuffle设置为False就好了,不做shuffle(每次 输出测试样本的 数据 及对它的预测 的时候,可以保证顺序是一样的,这对我们观察结果很有帮助~)
注:关于手写数字的识别,这个将会在下面的多分类中实现。
注:关于“泰坦尼克号”的作业,这个后续会补充说明!
1.7.5 练习(1)【建议取num_workers=0;若=2,速度反而慢了】
建议这里取 num_workers=0,若=2虽然也能Run,可速度却反而慢了,所以这里不要使用CPU多线程。下面有我测试的例子。
# 昵 称:XieXu
# 时 间: 2023/2/17/0017 18:16
import torch
import numpy as np
from torch.utils.data import Dataset # DataSet是抽象类,无法实例化
from torch.utils.data import DataLoader # DataLoader可实例化
class DiabetesDataset(Dataset):
def __init__(self, filepath):
xy = np.loadtxt(filepath, delimiter=',', dtype=np.float32)
self.len = xy.shape[0] # 获得数据集长度
self.x_data = torch.from_numpy(xy[:, :-1]) # 前8列,X输入(特征)
self.y_data = torch.from_numpy(xy[:, [-1]]) # 最后一列,Y结果(类别)
# 获得索引方法
def __getitem__(self, index):
return self.x_data[index], self.y_data[index]
# 获得数据集长度
def __len__(self):
return self.len
dataset = DiabetesDataset('diabetes.csv')
# num_workers表示多线程的读取。下面可通过train_loader获得(X,Y)元组,其中会自动把它们转为矩阵形式(根据batch_size数量),也是Tensor
train_loader = DataLoader(dataset=dataset, batch_size=32, shuffle=True, num_workers=2)
# 建议num_workers=0,这样反而会秒得结果。很快。不要取num_workers=2!2023.2.18 09:21
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self.linear1 = torch.nn.Linear(8, 6)
self.linear2 = torch.nn.Linear(6, 4)
self.linear3 = torch.nn.Linear(4, 1)
self.sigmoid = torch.nn.Sigmoid()
def forward(self, x):
x = self.sigmoid(self.linear1(x))
x = self.sigmoid(self.linear2(x))
x = self.sigmoid(self.linear3(x)) # 这里需要是sigmoid哦!2023.2.18 08:32
return x
model = Model()
# criterion = torch.nn.BCELoss(size_average=True) # UserWarning: size_average and reduce args will be deprecated, please use reduction='mean' instead.
criterion = torch.nn.BCELoss(reduction='mean') # 2023.2.17 18:18
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
# 100轮,loss=0.715 (每次不一样啦~)
# 1000轮,loss=0.38
# 500轮,loss=0.49
# 1000轮,lr=0.8,loss=0.35
if __name__ == '__main__':
for epoch in range(100):
for i, data in enumerate(train_loader, 0): # enumerate:可获得当前迭代的次数
# 准备数据dataloader会将按batch_size返回的数据整合成矩阵加载
inputs, labels = data
# 前馈(求y_hat,即 概率) 2023.2.18 08:39
y_pred = model(inputs)
loss = criterion(y_pred, labels)
print(epoch, i, loss.item())
# 反向传播(反馈)
optimizer.zero_grad()
loss.backward()
# 更新
optimizer.step()
初次训练:
可以看到,一轮训练,24次是什么意思呢?这是由于,是执行了24次 batch_size为32的数据,即【一个epoch就是过一遍所有数据,这个24就是取了24次batchsize为32的数据,也就是说数据一共有32 * 24 =768条或者少于768、大于 736= 32 * 23。我们知道,该糖尿病数据集中的样本数量为759。736< 759 <768,759/32=23.71875,故最少 只能执行24次batch_size=32 的数据才OK】以下图中的0 0 为例,这一竖列 0 代表 第0轮,然后,后面紧跟着的0,表示训练第0个batch_size,即取出32个样本训练(这应该是之前已经通过 DataLoader 划分好的),

结果。经过测试,num_workers=2 时,我觉得时间还行,用的不是特别多,大概需要2、3分钟吧。

这里再测试一下,num_workers=0,即不使用CPU多线程:
好吧,结果是秒得结果,这比起上面要快的多:【看到有朋友说:不要在DataLoader中使用多个worker,把num_workers设为0】
同样地,也是取num_workers=0,既然训练很快,那1000轮试试:loss=0.38,效果好了一些。
至于进一步优化,en…大家可以再试试 调整 lr学习率、optimizer优化器、激活函数 等等其它参数。
如调整lr=0.8,还是1000轮:loss=0.35,效果又好了一点点。
1.7.6 练习(2),划分训练集、测试集;封装训练过程、测试过程
与练习(1)类似,学习时建议先以(1)为准。
这里不同之处 在于 对数据集进行了划分,并将训练 和 测试 都做了封装,另外,训练50000轮,训练一直在进行,并每当训练过了2000轮时 便 执行 一次测试。
# 昵 称:XieXu
# 时 间: 2023/2/18/0018 9:32
# 1、将原始数据集分为 训练集和测试集
# 2、对训练集进行 批量梯度下降
# 3、评估测试集的准确率
import torch
import numpy as np
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
from sklearn.model_selection import train_test_split
# 读取原始数据,并划分训练集和测试集
raw_data = np.loadtxt('diabetes.csv', delimiter=',', dtype=np.float32)
X = raw_data[:, :-1]
y = raw_data[:, [-1]]
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X, y, test_size=0.3)
Xtest = torch.from_numpy(Xtest)
Ytest = torch.from_numpy(Ytest)
# 将训练数据集进行批量处理
# prepare dataset
class DiabetesDataset(Dataset):
def __init__(self, data, label):
self.len = data.shape[0] # shape(多少行,多少列)
self.x_data = torch.from_numpy(data)
self.y_data = torch.from_numpy(label)
def __getitem__(self, index):
return self.x_data[index], self.y_data[index]
def __len__(self):
return self.len
train_dataset = DiabetesDataset(Xtrain, Ytrain)
train_loader = DataLoader(dataset=train_dataset, batch_size=32, shuffle=True, num_workers=0) # num_workers 多线程
# design model using class
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self.linear1 = torch.nn.Linear(8, 6)
self.linear2 = torch.nn.Linear(6, 4)
self.linear3 = torch.nn.Linear(4, 2)
self.linear4 = torch.nn.Linear(2, 1)
self.sigmoid = torch.nn.Sigmoid()
def forward(self, x):
x = self.sigmoid(self.linear1(x))
x = self.sigmoid(self.linear2(x))
x = self.sigmoid(self.linear3(x))
x = self.sigmoid(self.linear4(x))
return x
model = Model()
# construct loss and optimizer
criterion = torch.nn.BCELoss(reduction='mean')
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
# training cycle forward, backward, update
def train(epoch):
train_loss = 0.0
count = 0
for i, data in enumerate(train_loader, 0):
inputs, labels = data
y_pred = model(inputs)
loss = criterion(y_pred, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
train_loss += loss.item()
count = i
if epoch % 2000 == 1999:
print("train loss:", train_loss / count, end=',')
def test():
with torch.no_grad(): # test,是不需要计算梯度的 2023.2.18 11:49。那么下面的执行 就不再计算梯度
y_pred = model(Xtest)
y_pred_label = torch.where(y_pred >= 0.5, torch.tensor([1.0]), torch.tensor([0.0]))
acc = torch.eq(y_pred_label, Ytest).sum().item() / Ytest.size(0)
print("test acc:", acc)
if __name__ == '__main__':
for epoch in range(50000):
train(epoch)
if epoch % 2000 == 1999:
test()
故一共执行了25次测试:这需要一些时间,大概几分钟

至于优化,大家可以去调试参数,同练习(1)。这里就不再冗余了。后面有时间的话,继续补充~
1.7.3 练习(3)使用GPU训练
基于练习(2),在拆分数据集为训练集和测试集的基础上,划分为 比例 0.8的训练集,0.2的测试集。此外,使用GPU训练。
# 昵 称:XieXu
# 时 间: 2023/2/18/0018 10:18
import numpy as np
import torch
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
from sklearn.model_selection import train_test_split
import pdb
# 定义一个cpu
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# 读取原始数据集,并且划分为训练集和测试集
xy = np.loadtxt('diabetes.csv', delimiter=',', dtype=np.float32)
x = xy[:, :-1]
y = xy[:, [-1]]
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3)
x_test = torch.from_numpy(x_test).to(device)
y_test = torch.from_numpy(y_test).to(device)
# prepare dataset
class DiabetesDataset(Dataset):
def __init__(self, data, labels):
# xy = np.loadtxt(filepath, delimiter = ',', dtype = np.float32)
self.len = data.shape[0] # shape(行,列)
self.x_data = torch.from_numpy(data)
self.y_data = torch.from_numpy(labels)
def __getitem__(self, index):
return self.x_data[index], self.y_data[index]
def __len__(self):
return self.len
train_dataset = DiabetesDataset(x_train, y_train)
train_loader = DataLoader(dataset=train_dataset, batch_size=32, shuffle=True, num_workers=0) # num_workers 多线程
# design model using class
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self.linear1 = torch.nn.Linear(8, 6)
self.linear2 = torch.nn.Linear(6, 4)
self.linear3 = torch.nn.Linear(4, 1)
self.sigmoid = torch.nn.Sigmoid()
def forward(self, x):
x = self.sigmoid(self.linear1(x))
x = self.sigmoid(self.linear2(x))
x = self.sigmoid(self.linear3(x))
return x
model = Model()
model.to(device)
# construct loss and optimizer
criterion = torch.nn.BCELoss(reduction='mean')
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
# optimizer = torch.optim.Adam(model.parameters(),
# lr=0.001,
# betas=(0.9, 0.999),
# eps=1e-08,
# weight_decay=0,
# amsgrad=False)
# training cycle forward, backward, update
def train(epoch):
train_loss = 0.0
count = 0.0
for i, data in enumerate(train_loader, 0): # start = 0,train_loader 是先shuffle后mini_batch
# inputs, labels = data
inputs, labels = data[0].to(device), data[1].to(device) # 使用gpu训练
y_pred = model(inputs)
loss = criterion(y_pred, labels)
# print(epoch, i, loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
train_loss += loss.item()
count = i
if epoch % 1000 == 999:
# pdb.set_trace()
print('epoch:', epoch + 1, 'train loss:', train_loss / count, end=',')
def test():
# 在with torch.no_grad()下对变量的操作,均不会让求梯度为真
with torch.no_grad():
y_pred = model(x_test)
y_pred_label = torch.where(y_pred >= 0.5, torch.tensor([1.0]).to(device), torch.tensor([0.0]).to(device))
acc = torch.eq(y_pred_label, y_test).sum().item() / y_test.size(0)
print('test acc:', acc)
if __name__ == '__main__':
for epoch in range(50000):
train(epoch)
if epoch % 1000 == 999: # 每训练 1000轮就执 行一次测试
test()
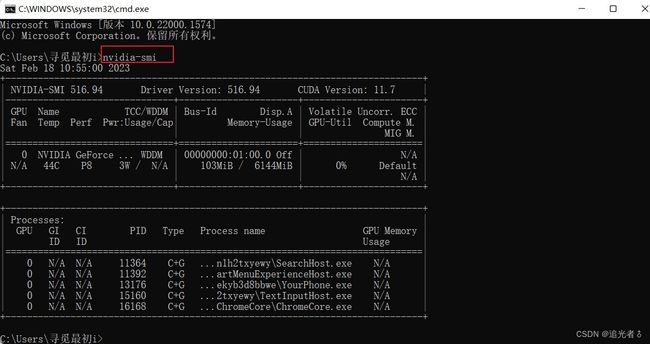
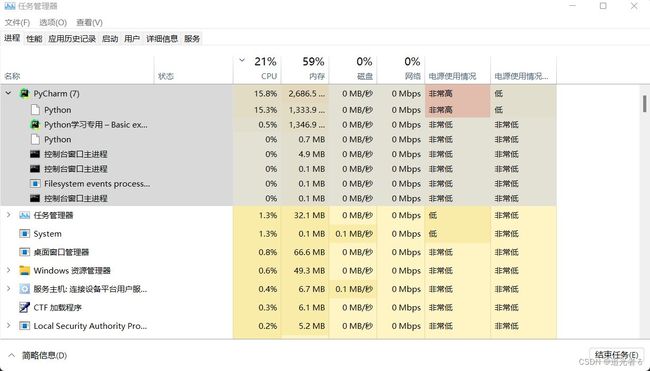
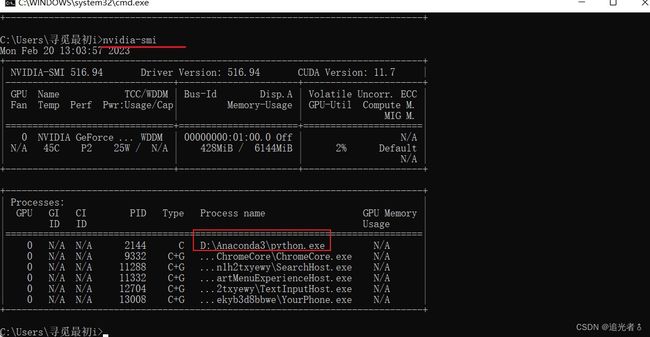
在训练过程中,可以 通过nvidia-smi查看一下,确实在使用GPU训练:

也可以这样看看:

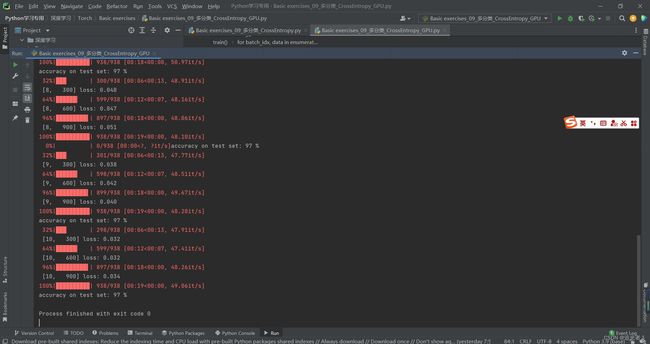
训练结果如下,这需要一些时间,由于每1000轮训练,就会执行一次测试,共训练50000轮,则会测试50次,所需的时间会比练习(2)要长。建议大家调试时,可以减少训练轮数,或者增加测试 所需的 训练间隔轮数等。以我目前的PC,大概Run30分钟。
1.8 多分类问题——交叉熵损失函数CrossEntropyLoss:Softmax分类器,One-hot;针对MNIST数据集
1.8.1 针对多分类问题,输出的概率 应满足“分布”的要求
回顾:
在此之前,我们针对糖尿病数据集,搭建了一个二分类网络。 y ^ \widehat {y} y 输出的是 当y=1时的概率值。因为只有两个分类,所以只需要 输出一个概率就行,另外一个概率,用1减去 当前求得的 y = 1 y=1 y=1时的概率就好。
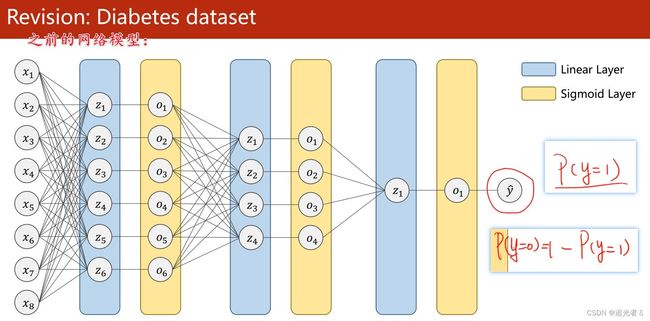
之前的网络模型:
而面对 像手写数字识别(MNIST数据集)这样的 多分类问题(0~9共10个数字,即10分类),我们在解决时,会用到softmax分类器。
本小节要解决的问题是:
- [1]
用softmax分类器来解决多分类问题; - [2] 在PyTorch中如何去实现;
针对多分类问题,输出的概率 应满足“分布”的要求:
一个思路是是采用之前的【二分类】来解决。即 将每一个分类作为二分类来判断。
例如 当输出为1时,对其他的 非1输出 都规定为0,以此来判断属于哪个类别。
但是,这种情况下,类别之间 所存在的互相抑制的关系没有办法体现,当一个类别出现的概率较高时,其他类别出现的概率仍然有可能很高。
也就是说,当计算输出为1的概率之后,再计算输出为2的概率时,并不是在输出为 非1的条件下进行的(即 计算输出为1的概率,并没有影响再计算输出为其它的概率),即 所有输出的概率之和实际上是大于1的。【有朋友说:每一个都看成二分类,是在单独计算每一种类别的概率! 各个类别判断之间 没有太多联系】
这里,我们希望,输出的概率满足 “分布”的性质要求。(通过Softmax就可完成)
- 第一, y ^ 1 \widehat y_{1} y 1到 y ^ 10 \widehat y_{10} y 10的输出,每一个 都得大于或等于0; 即 P ( y = i ) ≥ 0 P(y=i) \geq 0 P(y=i)≥0
- 第二, y ^ 1 \widehat y_{1} y 1到 y ^ 10 \widehat y_{10} y 10 这些概率求和,等于1。即 ∑ i = 0 9 P ( y = i ) = 1 \sum_{i=0}^{9} P(y=i) = 1 ∑i=09P(y=i)=1
这样才满足离散分布的要求。才真正算出了 样本属于 各个分类的 概率分布。
(对于分类问题,输出的 是个分布!二分类里 之所以 输出一个就行,是因为 只需要 y = 1 y=1 y=1的概率就行了, y = 0 y=0 y=0的概率可以用1减)
1.8.2 Softmax 计算公式
----(Softmax 其公式 就是用来将多个Linear之后得到的值 (多个类别 对应的值,是过程值,不是最终值),进行映射,只是映射为[0,1]的值,且这些值 加和=1。)----简言之:通过Softmax 得到多分类问题 中 概率分布
Z i Z_i Zi表示最后一层线性层的输出(各个类别 经过多层Linear 以及Sigmoid之后的过程值);
softmax函数为:
P ( y = i ) = e z i ∑ j = 0 K − 1 e z i , i ∈ { 0 , ⋯ , K − 1 } P(y=i)=\frac{e^{z_i}}{\sum_{j=0}^{K-1}e^{z_i}}, i \in \{0,{\cdots},K-1\} P(y=i)=∑j=0K−1eziezi,i∈{0,⋯,K−1}
分子是 以e为底的指数函数,取值是大于0的。也就是说,将每个类别 经过这些Linear层最终得到的值(当然这里边是有正有负的),通过上面的公式,映射为一个0~1的数(所属各个类别(分类)的概率),而它们加起来 和为1。(刚刚说过了,又啰嗦一下啦 ~)
例如,就像下面这样 若有3个分类:(注:最后一层不使用sigmoid了,而是 直接输入到softmax函数中。因此softmax 的输入可能有负值,但没关系!直接执行即可)
![]()
这样,才是最终的 y ^ \widehat y y 。
小结:
softmax的 输入参数 不需要 再做非线性变换,即softmax之前不再需要激活函数(relu)。
softmax两个作用:
- 1、如果在进行softmax前的input有负数,通过指数变换,得到正数;
- 2、使所有类别的概率求和为1(归一化/映射为0~1的值)。
对于多分类问题输出,Softmax会先对所有输出进行指数运算,以满足(1)要求(得到正数),再对结果进行归一化处理,以满足(2)要求。
1.8.3 通过softmax得到概率分布后,损失函数Loss如何做?
这里,先不做过多解释,直接给出损失函数:
L o s s ( Y ^ , Y ) = − Y l o g Y ^ Loss(\widehat Y,Y) = -Ylog \widehat Y Loss(Y ,Y)=−YlogY
由公式 结合 下图知:对通过softmax得到的概率分布,再对这些概率取对数,然后与编码进行运算即可。显然,只有一项取标签为1的,其它都是与标签0相乘。
模拟实现如下:可以看到 loss输出如 注释。给出了通过softmax计算得到概率分布 以及 如何计算损失的过程。【实际处理的时候,0项会直接忽略掉。如:若类别为1,那么会直接找到类别为1的索引,取对数,再进行Loss计算即可】
# 昵 称:XieXu
# 时 间: 2023/2/18/0018 21:58
# 测试实现
import numpy as np
y = np.array([1, 0, 0])
z = np.array([0.2, 0.1, -0.1])
y_pred = np.exp(z) / np.exp(z).sum() # 即 softmax的过程
# print(y_pred) # 即概率分布 [0.37797814 0.34200877 0.28001309]
loss = (-y * np.log(y_pred)).sum() # 即 损失函数
print(loss) # 0.9729189131256584
(闲话:由于是多分类,用Softmax替换之前普通的Sigmoid激活函数)
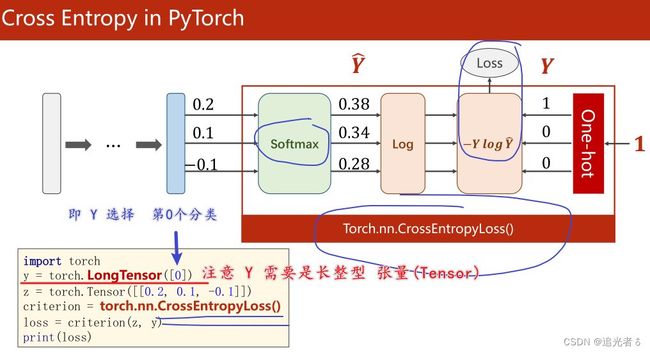
1.8.4 交叉熵损失CrossEntropyLoss = Softmax + 原Loss(即 − Y l o g Y ^ -Y log\widehat Y −YlogY )
值得注意的是:上述代码 封装在 CrossEntropyLoss()函数中,即可直接调用!
因此,在使用交叉熵损失的时候,注意 神经网络的最后一层 是不要做激活的,因为 将其变为概率分布的激活(Softmax) 是包含在 CrossEntropyLoss 中的!(Linear最后一层的结果 直接传入 CrossEntropyLoss 内做激活啦!得到概率分布,再进行log,然后求损失…)
故最后一层不用做非线性变换,直接交给交叉熵损失就行啦!!
import torch
y = torch.LongTensor([0]) # 老师解释,这里选的是第0个分类。(我测试过,这里和我们设定的值有关,可以填0/1/2,一共就三类,填3及以上就会报错)
z = torch.Tensor([[0.2, 0.1, -0.1]])
criterion = torch.nn.CrossEntropyLoss()
loss = criterion(z, y)
print(loss) # tensor(0.9729)
这里,再看一个具体的例子:结合我写的注释理解 即可~
# 2023.2.18 23:25
import torch
criterion = torch.nn.CrossEntropyLoss()
Y = torch.LongTensor([2, 0, 1]) # 有3个样本,分别属于 第2类 第0类 第1类
# 下面有两组不同的预测
Y_pred1 = torch.Tensor([[0.1, 0.2, 0.9], # 0.9最大,经过softmax之后也会比较大 符合第2类
[1.1, 0.1, 0.2], # 1.1最大,同理,符合第0类
[0.2, 2.1, 0.1]]) # 2.1最大,同理,符合 第1类
Y_pred2 = torch.Tensor([[0.8, 0.2, 0.3], # 第0类 这与实际的Y 不符
[0.2, 0.3, 0.5], # 第2类 这也与实际的Y不符
[0.2, 0.2, 0.5]]) # 第2类 这也与实际的Y不符
l1 = criterion(Y_pred1, Y)
l2 = criterion(Y_pred2, Y)
print("Batch Loss1 = ", l1.data, "\nBatch Loss2=", l2.data)
'''输出如下:
Batch Loss1 = tensor(0.4966) # 可以从上边的样本看出,loss是比较小的,因为样本的取值大小 是和 上面Y的类别 符合的!
Batch Loss2= tensor(1.2389) # 而这里损失就大一些。结合上边第二个预测,确实和实际的Y不符,有差别,所以损失大~
'''
附:交叉熵损失 和 NLLLoss之间有什么差别,可参阅文档如下,
- https://pytorch.org/docs/stable/nn.html#crossentropyloss
- https://pytorch.org/docs/stable/nn.html#nllloss
取决于需求,有时候会用NLLLoss,有时候会直接用交叉熵CrossEntropyLoss。
1.8.5 有了上面的分析,这里如何处理MNIST数据集呢
上面几个小节 记录过的神经网络中,输入 X X X都是向量。这里的数据集,是图像数据。下面是MNIST数据集中的一张手写数字的图像。【如下左图,颜色越深,就表明数值是0,越亮的地方,就表明数值越大。这在右侧图中可以看出来】

每个数字都是一个 28 ∗ 28 = 784 28*28=784 28∗28=784大小的灰度图(784个像素,每个像素的取值是0~255),可将灰度图中的每个像素值映射到 ( 0 , 1 ) (0,1) (0,1)区间内(0即0,255即1),就是上面的右图 ( 28 ∗ 28 28*28 28∗28的矩阵)。数值大的 用深颜色,数值小一些的,用浅颜色。
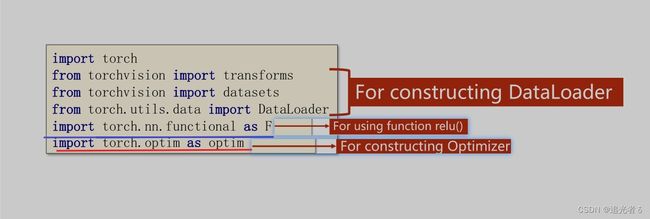
导入一些工具包:
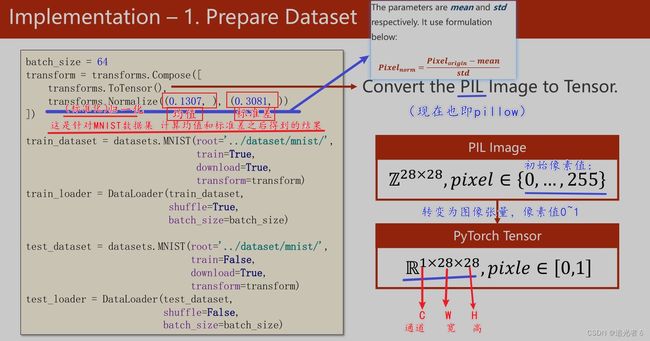
- 维度 由 28 ∗ 28 28*28 28∗28 转换为 1 ∗ 28 ∗ 28 1*28*28 1∗28∗28形式的张量(Tensor),即由单通道变为多通道;
- 将(0,255) 转换为 (0,1)浮点数的形式,即0 1 分布;
以供神经网络进行训练。【0 1 分布的数据给神经网络训练是最好的!】
并且,定义好transform变换以后,直接 将其放到数据集里面,(读取第i个数据样本的时候,拿到的数据会直接 经transform处理)
即:通道放前边,为了 更高效地 进行图像处理、卷积运算而做的转换~

如 四六级成绩的计算(假设):希望将成绩映射为(0,1)的正态分布。【0,1分布指的是 均值为0,标准差为1的正态分布。N(0,1)是标准正态分布】
附:百度知道——N(0,1)分布是什么分布?

1.8.6 模型
激活层改用ReLU激活函数;
最后的输出层不做激活,因为是由交叉熵损失去计算softmax。
此外,还要通过view 转换为矩阵。
具体地,如下图:(下图中, N N N可理解为batch_size)
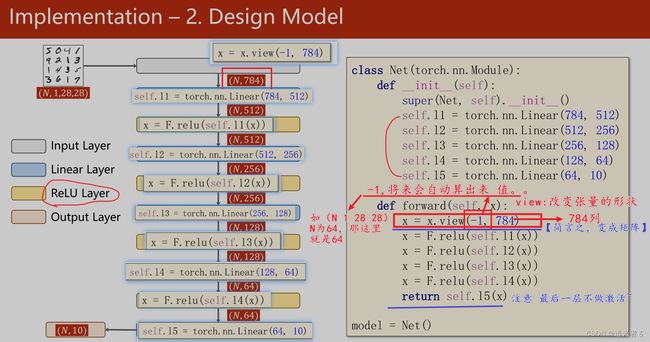
交叉熵损失;
梯度下降中,使用“冲量”momentum,来优化训练过程。(大概作用:冲破局部极小值;给数据一个惯性值,可以从局部极值走出来,尽可能找到全局最优解)

封装训练过程;
每300次迭代,输出一次running_loss。

test里,不需要进行反向传播;不需要计算梯度;
只需要算正向的,算一下分类算对了多少~
具体,如下:
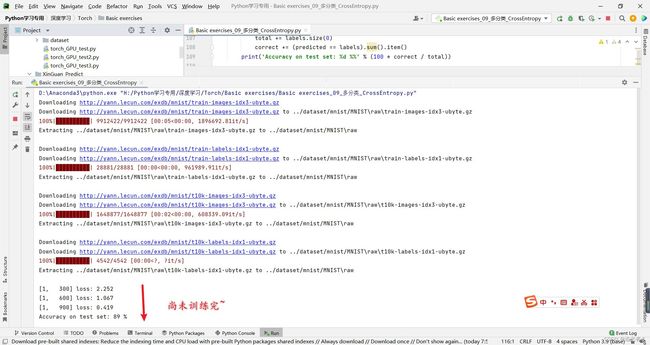
1.8.7 练习(1)(未使用GPU)默认CPU
# 昵 称:XieXu
# 时 间: 2023/2/18/0018 11:58
# 针对手写数字数据集MNIST
import torch
# 组建DataLoader
from torchvision import transforms # 针对 图像 进行处理 2023.2.18 23:57
from torchvision import datasets
from torch.utils.data import DataLoader
# 激活函数和优化器
import torch.nn.functional as F # For using function relu() 2023.2.18 23:58
import torch.optim as optim
# Dataset&Dataloader必备
batch_size = 64
# pillow(PIL)读的原图像格式为W*H*C,原值较大
# 转为格式为C*W*H,值为0-1的Tensor
transform = transforms.Compose([
# 变为格式为C*W*H的Tensor
transforms.ToTensor(),
# 第一个是均值,第二个是标准差,变值为0-1
transforms.Normalize((0.1307,), (0.3081,))
])
train_dataset = datasets.MNIST(root='../dataset/mnist/',
train=True,
download=True,
transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist/',
train=False,
download=True,
transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
# 线性层1,input784维 output512维
self.l1 = torch.nn.Linear(784, 512)
# 线性层2,input512维 output256维
self.l2 = torch.nn.Linear(512, 256)
# 线性层3,input256维 output128维
self.l3 = torch.nn.Linear(256, 128)
# 线性层4,input128维 output64维
self.l4 = torch.nn.Linear(128, 64)
# 线性层5,input64维 output10维
self.l5 = torch.nn.Linear(64, 10)
def forward(self, x):
# 改变张量形状view\reshape
# view 只能用于内存中连续存储的Tensor,transpose\permute之后的不能用
# 变为二阶张量(矩阵),-1用于计算填充batch_size
x = x.view(-1, 784)
# relu 激活函数
x = F.relu(self.l1(x))
x = F.relu(self.l2(x))
x = F.relu(self.l3(x))
x = F.relu(self.l4(x))
# 注:第五层 不可以 再进行relu激活 2023.2.18 19:33。交叉熵损失 CrossEntropyLoss 已经包含激活啦!
# 第五层 不用再 显式地 用激活函数 处理 映射了~
# 交叉熵损失 CrossEntropyLoss 已经包含激活 对五层的值 激活啦!softmax得概率分布呗,之后再求损失(也是封装到CrossEntropyLoss内了)
# 即 第五层(最后一层) 的结果直接 送到 CrossEntropyLoss 求损失函数即可!! 2023.2.18 22:46
return self.l5(x) # 因此,直接将 第五层得到的结果 送入CrossEntropyLoss即可!!后续再其内 会激活(Softmax)滴! 2023.2.18 22:49
model = Net()
# Loss&Optimizer
# 交叉熵损失
criterion = torch.nn.CrossEntropyLoss()
# 随机梯度下降,momentum表冲量,在更新时一定程度上保留原方向
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)
def train(epoch):
running_loss = 0.0
# 提取数据
for batch_idx, data in enumerate(train_loader, 0):
inputs, target = data
# 优化器清零
optimizer.zero_grad()
# 前馈+反馈+更新
outputs = model(inputs)
loss = criterion(outputs, target)
loss.backward()
optimizer.step()
# 累计loss
running_loss += loss.item()
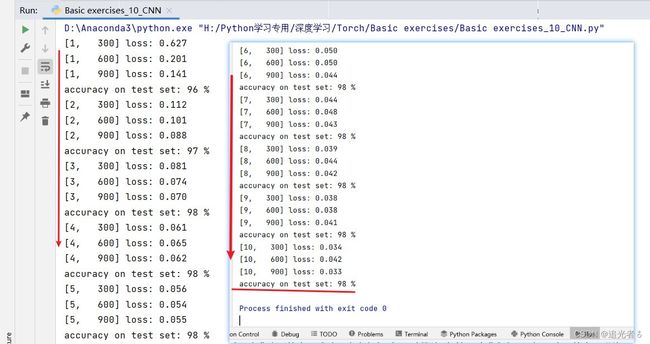
if batch_idx % 300 == 299:
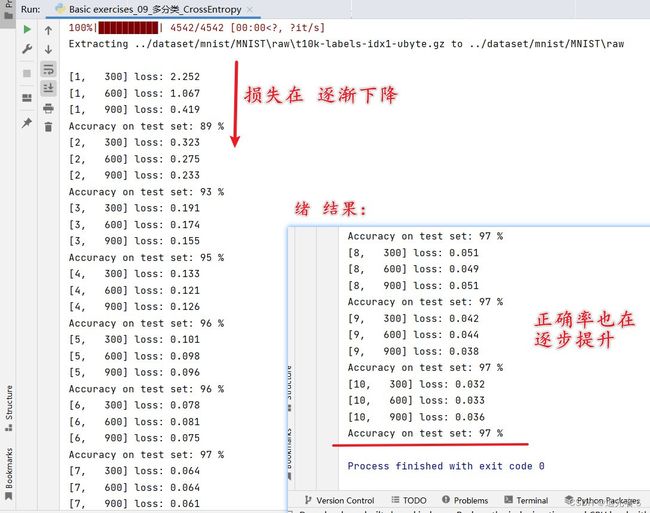
print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
running_loss = 0.0
def test():
correct = 0
total = 0
# 避免计算梯度
with torch.no_grad():
for data in test_loader:
images, labels = data
outputs = model(images)
# 取每一行(dim=1表第一个维度)最大值(max)的下标(predicted)及最大值(_)
_, predicted = torch.max(outputs.data, dim=1)
# 加上这一个批量的总数(batch_size),label的形式为[N,1]
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('Accuracy on test set: %d %%' % (100 * correct / total))
if __name__ == '__main__':
for epoch in range(10):
train(epoch)
test()
初次Run时,会下载MNIST数据集(也可以自己事先准备好):
(到了97%,很难再上升了。这是由于 全连接的神经网络 对于图像处理分析,对局部信息的利用 做的并不是非常好。所有的元素都做了全连接,即 图像中的一个元素 与其它任何一个位置的元素 都要产生联系…权重不够多;在处理图像的时候,我们更关注 高抽象级别的特征,而这里我们用的是 非常原始的特征。因此 用某些特征提取,做分类训练,可能效果会更好一些;或者自动进行特征提取,如CNN)
1.8.8 练习(2)使用GPU
与练习(1)类似,仅仅添加/修改了使用GPU的代码。
# 昵 称:XieXu
# 时 间: 2023/2/18/0018 21:15
# 使用GPU加速
# 尚未执行
''' 手写字符识别pytorch实现 '''
import torch
from torchvision import transforms, datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
from tqdm import tqdm
# 定义一个cpu
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# prepare dataset
batch_size = 64
# 图像预处理
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))]) # 归一化,两个值是均值和方差
train_dataset = datasets.MNIST(root='../dataset/mnist/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist/', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)
# design model using class
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.l1 = torch.nn.Linear(28 * 28, 512)
self.l2 = torch.nn.Linear(512, 256)
self.l3 = torch.nn.Linear(256, 128)
self.l4 = torch.nn.Linear(128, 64)
self.l5 = torch.nn.Linear(64, 10)
def forward(self, x):
x = x.view(-1, 784) # 将N*1*28*28的图片转换成N*1*784,-1代表N的值,即自动获取mini_batch
x = F.relu(self.l1(x))
x = F.relu(self.l2(x))
x = F.relu(self.l3(x))
x = F.relu(self.l4(x))
return self.l5(x) # 最后一层不做激活,直接接到softmax
model = Net()
model.to(device)
# construct loss and optimizer
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.5)
# training cycle forward, backward, update
def train(epoch):
running_loss = 0.0
for batch_idx, data in enumerate(tqdm(train_loader), 0): # tqdm是一个快速的,易扩展的进度条提示模块 2023.2.19 01:50
inputs, labels = data[0].to(device), data[1].to(device) # 使用gpu训练
optimizer.zero_grad()
# forward + backward + optimize
# 获得模型预测结果(64, 10)
outputs = model(inputs)
# 交叉熵代价函数outputs(64,10),target(64)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
if batch_idx % 300 == 299: # 输出每次的平均loss
print('\n [%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
running_loss = 0.0
def test():
correct = 0
total = 0
with torch.no_grad():
for data in test_loader:
images, labels = data[0].to(device), data[1].to(device)
outputs = model(images)
_, predicted = torch.max(outputs.data, dim=1) # 并不关心最大值是多少,用下划线来存,需要在意的是index,
# dim=1表示输出所在行的最大值,若改写成dim=0则输出所在列的最大值。
total += labels.size(0) # N*1
correct += (predicted == labels).sum().item() # 张量之间的比较运算
print('accuracy on test set: %d %% ' % (100 * correct / total))
if __name__ == '__main__':
for epoch in range(10):
train(epoch)
test()
nvidia-smi查看运行过程中是否使用了GPU:
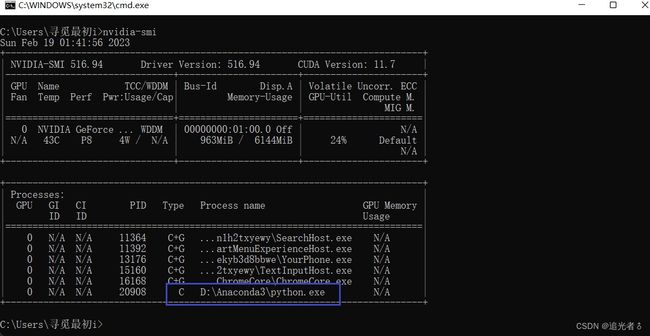
CPU和内存情况:比起使用CPU来运行,这样好多了!CPU占用很少了~
1.9 卷积神经网络CNN(基础篇)
1.9.1 基础概念:卷积、卷积运算过程、单通道卷积&多通道卷积、卷积层 权重 w w w的四个维度
CNN,比起一维信息的Linear线性层,可以保留图像的空间特征。
卷积神经网络,即 Convolutional Neural Network。
在上一目录,介绍了全连接神经网络。所谓全连接,即网络中使用的全都是线性层Linear。如果网络是由全连接层串行起来,就称之为全连接网络。
每一个输入节点,都要参与到下一层的计算上。这样也叫全连接,Fully Connected。作为下一层而言,每一个输入值 和 每一个输出值之间都存在权重。
在全连接层中,实际上是把原先空间状态上的信息,转换为了一维的信息,使得 原有的 空间相对位置 所蕴含的信息丢失。而卷积神经网络中,可以保留图像的空间特征(信息)。
卷积,实际上是把 原始图像 仍然按照 空间的结构 来进行保存数据。
- 特征提取阶段:直接对图像做
卷积运算,提取特征; - 转换为向量,
经过全连接神经网络,再做分类;
![]()
卷积
1×28×28 指的是 C ( c h a n n l e ) × W ( w i d t h ) × H ( H i g h t ) C(channle) \times W(width) \times H(Hight) C(channle)×W(width)×H(Hight)
即通道数 × \times × 图像宽度 × \times × 图像高度,通道可以理解为层数,通过同样大小的多层图像堆叠才形成了最原始的图。
我们拿到的图像,要分成红、绿、蓝三个通道,即Channel。
如下图所示,对一个 3 × W × H 3 \times W \times H 3×W×H的原始图像,卷积的处理是每次对其中一个Patch进行处理,也就是从原数图像的左上角开始依次抽取一个 3 × W ′ × H ′ 3 \times W' \times H' 3×W′×H′的图像对其进行卷积,输出一个 C ′ × W ′ ′ × H ′ ′ C' \times W'' \times H'' C′×W′′×H′′的子图。
(可以抽象的理解成原先的图是一个立方体性质的,卷积是将立方体的长宽高按照新的比例进行重新分割而成的)
单通道卷积( 1 × W × H 1 \times W \times H 1×W×H):即 对于规格为 1 × W × H 1 \times W \times H 1×W×H的原图,利用一个规格为 1 × W ′ × H ′ 1 \times W' \times H' 1×W′×H′的卷积核进行卷积处理的数乘操作。
从原始数据的左上角开始 依次选取与核的规格相同( 1 × W ′ × H ′ 1 \times W' \times H' 1×W′×H′)的输入数据进行数乘操作,并将求得的数值作为一个Output值进行填充。
![]()
多通道卷积( N × W × H N \times W \times H N×W×H):通常是许多个通道。以三通道为例:红、绿、蓝 三个通道分别和不同的卷积核做卷积(每个通道 都配一个核~,所以通道数和卷积核的数目 是相同的),先是得到如下结果,

因此,同样的道理,若输入是 N N N个通道:卷积核的数目也是 n n n个,即 n × 3 × 3 n \times 3 \times 3 n×3×3的张量,输出的通道数为 1 1 1。

若想要 输出的 c h a n n e l = m channel=m channel=m,类比上边,只需要 让输入 的channel 再与 卷积核 运算,这样就又可以得到 一个输出channel啦!如下图举例:
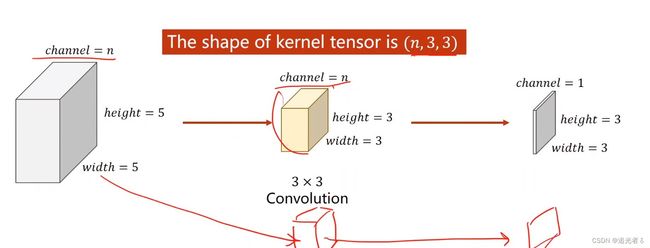
故,准备 m m m 批(组) 卷积核这样的卷积核,就得到输出的channel数为 m m m啦!就可以得到 m m m个输出通道。

进一步地,把得到的这些通道 拼接(Cat)起来,按照得到通道的顺序依次拼接起来就好:
- 每个卷积核,通道数量 要求和 输入数量是一样的;
- 这种卷积核数量有多少个,是和 输出通道数 是一样的;
- )
至于卷积核大小,是3x3的、5x5、还是7x7的等,那是自己定义的,这和图像大小是没关系的。
“卷积核就是这么大的”,在对每一个图像块 做运算时,用的都是相同的卷积核,即“共享权重”的机制。
进一步地,可将m个卷积核 拼成一个4维的张量:

因此,构建卷积层,其权重 要包括四个维度:输出维度、输入维度、卷积核宽度、卷积核高度。
1.9.2 CNN计算过程示例
# 昵 称:XieXu
# 时 间: 2023/2/19/0019 15:14
# 卷积计算 示例
import torch
# 即 n,m
in_channels, out_channels = 5, 10 # 定义 input channel输入通道数、output channel 输出通道数 2023.2.19 15:15
width, height = 100, 100 # 图像大小
kernel_size = 3 # 卷积核大小,默认转为3*3,最好用奇数正方形。(PyTorch中 卷积运算用偶数也可) 2023.2.19 15:32
# 在PyTorch中,所有的输入数据,必须是 小批量数据 2023.2.19 15:17
# 因此对于C*W*H的三个维度图像,在代码中实际上是一个B(batch)*C*W*H的四个维度的图像
batch_size = 1
# 生成一个四维的随机数(满足正态分布采样的 随机数) 2023.2.19 15:19
input = torch.randn(batch_size, # batch 小批量
in_channels, # n
width, # w
height) # h
# Conv2d必须 设定,输入输出的通道数以及卷积核尺寸
conv_layer = torch.nn.Conv2d(in_channels, # 输入通道的数量 n
out_channels, # 输出通道的数量 m
kernel_size=kernel_size) # 卷积核大小(尺寸) 如3*3。也可以自己指定元组 如(5,5)等
output = conv_layer(input)
print(input.shape)
print(output.shape)
print(conv_layer.weight.shape)
1.9.3 改进——padding,一般 外围补0
开始时,输入5x5维度,经过3x3的卷积核,我们能得到输出的维度 是3x3。

如果还是想要得到5x5的维度,就需要在原始的输入外围进行填充。
即若对于一个大小为 N × N N \times N N×N的原图,经过大小为 M × M M \times M M×M的卷积核卷积后,仍然想要得到一个大小为 N × N N \times N N×N的图像,则需要对原图进行Padding,即外围填充。
具体而言,对于一个 5 × 5 5 \times 5 5×5的原图,若想使用一个 3 × 3 3 \times 3 3×3的卷积核进行卷积,并获得一个同样 5 × 5 5 \times 5 5×5的图像,则需要进行Padding=1,即填充一圈,通常外围填充0。
(若卷积核大小为5x5的,那就得再填充一圈,才能保持计算之后,输出的维度和输入的维度同~)
一般情况下,
卷积核3x3——padding=1圈(3/2=1,整除哈!)卷积核5x5——padding=2圈(5/2=2,整除哈!是一个这种规律,这样算即可)
对于上图的实现:
# 昵 称:XieXu
# 时 间: 2023/2/19/0019 16:12
# padding练习
import torch
input = [3, 4, 6, 5, 7,
2, 4, 6, 8, 2,
1, 6, 7, 8, 4,
9, 7, 4, 6, 2,
3, 7, 5, 4, 1]
# 将输入变为B*C*W*H
input = torch.Tensor(input).view(1, 1, 5, 5) # 1 1 5 5 ,分别是batch,Channel,Width,Height 2023.2.19 16:14
# 偏置量bias置为false。输入 和 输出 都只有1个通道~
conv_layer = torch.nn.Conv2d(1, 1, kernel_size=3, padding=1, bias=False) # bias 会在卷积后 给 每个通道 加偏置量,但这里不需要加偏置
# 将卷积核变为CI*CO*W*H
kernel = torch.Tensor([1, 2, 3, 4, 5, 6, 7, 8, 9]).view(1, 1, 3, 3) # 1 1 3 3 分别是输出通道数、输入通道数、宽度、高度
# 将做出来的 卷积核张量,赋值 给 卷积运算中的 权重(参与卷积计算)
conv_layer.weight.data = kernel.data
output = conv_layer(input)
print(output)
# print(output.data) # 亦可
结果如下,与上图中是一样的。
(卷积,本质上依然是 线性计算.)
1.9.4 改进——步长 stride
【可以有效降低feature map 的宽度和高度】
练习:
依然是针对上面1.9.3的代码,不添加padding,添加stride=2,即:
conv_layer = torch.nn.Conv2d(1, 1, kernel_size=3, stride=2, bias=False) # stride步长练习
结果:
1.9.5 改进——下采样(又叫“池化”),一般采用 Max Pooling Layer
下采样,用的比较多的,一般可采用“最大池化”,Max Pooling Layer。
最大池化层,是没有权重的。
如使用 2x2的 Max Pooling ,注意 它默认 stride=2。
做 Max Pooling 时,只是对于通道做 最大池化,通道之间不会去找最大值。
故 通道数量不变。但,如,若使用 2x2 的 MaxPooling,图像大小会变为原来一半~
练习:
# 昵 称:XieXu
# 时 间: 2023/2/19/0019 17:16
# 最大池化 MaxPooling 练习
import torch
input = [3, 4, 6, 5,
2, 4, 6, 8,
1, 6, 7, 8,
9, 7, 4, 6]
input = torch.Tensor(input).view(1, 1, 4, 4)
# kernel_size=2 则 MaxPooling中的Stride也会被 默认设置为2
maxpooling_layer = torch.nn.MaxPool2d(kernel_size=2)
output = maxpooling_layer(input)
print(output)
1.9.6 针对MNIST数据集,所采用的模型
整体上,采用的CNN模型如下:

(卷积本质上 也是线性运算,不加激活函数的话,多层卷积 相当于 多层线性运算,没有意义。即 加入激活函数 是为了引入非线性(因素),让网络更复杂,处理提取的特征更多)
下图,简言之,(卷积以后,先ReLU,再做 最大池化;再卷积,ReLU激活,最大池化。view改变形状,再接 全连接层 )
![]()
降到10维之后,就和数字图像的输出对应上了,然后传到 交叉熵损失函数,获得损失,进行训练。
下图,右边的代码里,是先做的池化MaxPooling,而后ReLU,和左图中相反了,这应该没关系,在结果上区别不大,下边我也测试过了。(有同学说,先池化,后ReLU,计算量小一些)(还有同学说,确实区别不大,只要激活函数在两次卷积之间就好了)
下面考虑将模型在GPU上来跑。
1.9.7 如何在GPU上来跑(怎么用显卡来计算)
【把运算迁移到GPU上】
首先是,把模型迁移到GPU上:
定义device:

模型迁移到GPU:即 将整个模型的参数、缓存以及所有的模块 都放到cuda里面,转成cuda Tensor。
即 输入 和 对应输出,(注意 迁移的device要和模型的device 要在同一块显卡上)
1.9.8 练习(1)
未使用GPU:
基于前几个目录,这里注释就不写太多了,可以自己看着理解一下,不明白的再往上翻…
# 昵 称:XieXu
# 时 间: 2023/2/19/0019 17:37
import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim
# prepare dataset
batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])
train_dataset = datasets.MNIST(root='../dataset/mnist/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist/', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)
# design model using class
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = torch.nn.Conv2d(1, 10, kernel_size=5)
self.conv2 = torch.nn.Conv2d(10, 20, kernel_size=5)
self.pooling = torch.nn.MaxPool2d(2)
self.fc = torch.nn.Linear(320, 10)
def forward(self, x):
# flatten data from (n,1,28,28) to (n, 784)
batch_size = x.size(0) # 张量.size,把维度拿出来 2023.2.19 19:19
x = F.relu(self.pooling(self.conv1(x)))
x = F.relu(self.pooling(self.conv2(x)))
x = x.view(batch_size, -1) # -1 此处自动算出的是320
# view()函数用来转换size大小,x = x.view(batch_size, -1)中batchsize指转换后有几行,
# 而-1根据原Tensor数据和batchsize自动分配列数~ 2023.2.19 19:27
x = self.fc(x)
return x
model = Net()
# construct loss and optimizer
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)
# training cycle forward, backward, update
def train(epoch):
running_loss = 0.0
for batch_idx, data in enumerate(train_loader, 0):
inputs, target = data
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, target)
loss.backward()
optimizer.step()
running_loss += loss.item()
if batch_idx % 300 == 299:
print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
running_loss = 0.0
def test():
correct = 0
total = 0
with torch.no_grad():
for data in test_loader:
images, labels = data
outputs = model(images)
_, predicted = torch.max(outputs.data, dim=1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('accuracy on test set: %d %% ' % (100 * correct / total))
if __name__ == '__main__':
for epoch in range(10):
train(epoch)
test()
# accuracy on test set: 98 %

结果如下:正确率 98%.(在目录 1.8中,使用全连接Linear来跑的时候,准确率是97%),看来,这样提升了一丢丢!
![]()
企业级理解如下:【老师讲到:不要去从 正确率的角度说,要从 错误率的角度说!错误率 由原来的3% 降到了 2%,这是降低一个百分点嘛?!不是!足足降低了1/3!!(错误率降低成 原来的2/3,有了30%多的改进!!)】够 “吹” 的啦!!
上述代码中,forward()里,先池化后ReLU。
这里再记录一下 先ReLU激活 后池化的效果,即:
def forward(self, x):
batch_size = x.size(0)
x = self.pooling(F.relu(self.conv1(x))) # 先ReLU 后池化也行~
x = self.pooling(F.relu(self.conv2(x)))
x = x.view(batch_size, -1)
x = self.fc(x)
return x
嗯…先ReLU激活,后池化,效果和之前差不多,也是98%:所以都行的~
1.9.9 练习(2)使用GPU来跑
基于目录1.9.7中如何添加GPU来跑,只是对1.9.8的代码 稍微添加即可:
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model.to(device)
inputs, target = inputs.to(device), target.to(device) # 添加该行 2023.2.19 20:16
images, labels = images.to(device), labels.to(device) # 添加改行
完整code如下(含绘图):
# 昵 称:XieXu
# 时 间: 2023/2/19/0019 19:38
# 在GPU上来跑
import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim
import matplotlib.pyplot as plt
# prepare dataset
batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])
train_dataset = datasets.MNIST(root='../dataset/mnist/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist/', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)
# design model using class
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = torch.nn.Conv2d(1, 10, kernel_size=5)
self.conv2 = torch.nn.Conv2d(10, 20, kernel_size=5)
self.pooling = torch.nn.MaxPool2d(2)
self.fc = torch.nn.Linear(320, 10)
def forward(self, x):
# flatten data from (n,1,28,28) to (n, 784)
batch_size = x.size(0)
x = F.relu(self.pooling(self.conv1(x)))
x = F.relu(self.pooling(self.conv2(x)))
x = x.view(batch_size, -1) # -1 此处自动算出的是320
# print("x.shape",x.shape)
x = self.fc(x)
return x
model = Net()
device = torch.device("cuda" if torch.cuda.is_available() else "cpu") # 添加改行
model.to(device) # 添加改行
# construct loss and optimizer
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)
# training cycle forward, backward, update
def train(epoch):
running_loss = 0.0
for batch_idx, data in enumerate(train_loader, 0):
inputs, target = data
inputs, target = inputs.to(device), target.to(device) # 添加该行 2023.2.19 20:16
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, target)
loss.backward()
optimizer.step()
running_loss += loss.item()
if batch_idx % 300 == 299:
print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
running_loss = 0.0
def test():
correct = 0
total = 0
with torch.no_grad():
for data in test_loader:
images, labels = data
images, labels = images.to(device), labels.to(device) # 添加改行
outputs = model(images)
_, predicted = torch.max(outputs.data, dim=1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('accuracy on test set: %d %% ' % (100 * correct / total))
return correct / total # 返回测试集的 正确率 2023.2.19 20:20
if __name__ == '__main__':
epoch_list = [] # 画图用,横轴坐标 2023.2.19 20:19
acc_list = [] # 纵轴坐标
for epoch in range(10):
train(epoch)
acc = test() # 得到该轮 的正确率~
epoch_list.append(epoch) # 横轴
acc_list.append(acc) # 纵轴
plt.plot(epoch_list, acc_list)
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.title("accuracy with epoch")
plt.show()
查看GPU使用情况:
来看结果:
1.10 卷积神经网络CNN(高级篇)
1.10.1 背景,引出更复杂的网络结构(非串行的)
在上面曾介绍过的 卷积神经网络CNN、多层感知机 全连接网络,它们在网络架构上是串行的结构,即当前层的输出 是 下一层的输入。
但是在神经网络中,有很多更为复杂的结构,在网络结构中会有分支,甚至说 某层的输出 可能还会 回过头来 继续作为输入。

回顾上一节:2个卷积层,2个池化层,后接 全连接层,然后得到输出~
下面介绍复杂一些的网络结构,不是串行的网络结构。
1.10.2 非串行网络结构 之 GoogLeNet
GoogLeNet网络结构:包括卷积(Convolution),池化(Pooling)、全连接(Softmax)以及连接(Other)四个部分。
那么根据编程经验,减少代码的冗余,第一要减少代码中的重复,(重复多了,有可能出错);
减少代码冗余,在 过程式编程泛型里,如C语言中 的“函数” 可以作为减少代码冗余的工具;在面向对象里面,我们可以通过构造 类 来减少代码冗余。
因此,观察上图中的模型,看有没有相似或相同的结构。
显然是有的,就像下面标注的 “蓝 蓝 红,四个蓝”,好多都是这种样式的:
即 把这种块 封装成一个类,然后再把 这些块 串起来!这样就能极大减少代码里 重复的工作。
1.10.3 GoogLeNet:Inception Module,Average Pooling, 1 × 1 1\times1 1×1卷积
在GoogLeNet中,把上述画起来的 那种块 叫做 Inception。
(有一部很著名的电影——《盗梦空间》,其英文名字即 Inception!)
注:Inception Module 有很多可以构造的方式,下面只是其中一种。以它为例来介绍。
构造成上述样式的原因是,在构造神经网络时,有些超参数是比较难选的,如卷积核Kernel大小,用3x3的,还是用5x5的?还是其它的?即 选择哪一个卷积核效果更好,比较困难。
GoogLeNet的出发点是,不知道哪个卷积核比较好用,那么,就在一个块里,把这几种卷积都用一下!然后把它们的结果放到一起,若3x3的卷积核好用,那么 它的权重就会比较大。而其它路线下,权重相对来讲就会变小。【即GoogLeNet提供了几种候选的 CNN的配置,通过训练,在以上几条路线中 自动地找到最优的组合】
Concatenate 用来将张量拼接起来,例如,下面 有两个张量,沿着通道,可将二者拼接起来,这就叫做Concatenate,拼接,
![]()
从四条路径出来的,是四个张量,卷积操作过后,需要再把它们拼接回一个张量。
要注意:在上述四个路径(四种方法)中,最终的输出图必须仍然保持相同的W(图像宽度)以及H(图像高度),否则无法再次进行拼接 传输到下一层模块中。(可以这样理解:沿着通道方向,宽高平面接在一起,所以要求宽高一致)
(我们知道,在上一目录中,进行最大池化时,会导致图像变为原来一半,因此要想保证图像大小不变,需要人为地指定 stride和padding值。在均值池化 Average Pooling这里也是如此,通过人为指定stride和padding值,来保证输入和输出的图像大小(W、H)是一致的)
此外,1x1卷积的个数取决于 输入张量的通道个数。
1x1卷积举例:显然,卷积过后,依然保持 3 × 3 3\times 3 3×3大小。多个通道,那么针对每一个通道 都要配一个卷积核。

做完卷积之后,同时也是要求和的:同样地,不管输入通道多少个,最后 加和过后 也都是 变成 1 × W × H 1 \times W \times H 1×W×H的 feature map。若 三个挪起来的卷积核有 m m m个,那么输出就可以得到 m m m个 1 × W × H 1 \times W \times H 1×W×H feature maps。
因此 1 × 1 1\times1 1×1的卷积 可以跨越不同通道相同位置 元素的值。 即 将它们的信息融合到一起了。【信息融合】。
为什么要使用 1 × 1 1\times1 1×1卷积?
主要作用: 1 × 1 1\times1 1×1卷积可以改变通道的数量。从而极大降低运算量。
下边举例来说明:
输入张量有192个通道,图像大小宽高 为 28 × 28 28\times 28 28×28,用 5 × 5 5\times5 5×5的卷积核 做卷积运算,padding=2 保证卷积过后 图像宽高不变,
那么,卷积运算进行的 浮点数运算量(次数)亦如下所示。5x5卷积,对每一个元素都进行运算,故乘以 2 8 2 28^2 282;每次卷积,实际上 是对所有通道来做的,因此再乘以192;这样的运算共做了32次,才能得到输出通道,故再乘以32。。可以看到,计算量(计算次数)超过 1亿两千万次…【注:深度学习中 问题之一 就是运算量太大,因此要想办法降低 运算量】
附,对于上面的计算,大家的问题:
[1] 不乘32的话,得到的就是一组卷积核卷积之后的结果,是单通道,需要32组卷积核才能出32通道 (多通道输出)。
[2] 一个卷积核生成一个特征图,右边共有32张特征图 组成,所以在此基础上 再乘32。
[3] 因为你要生成32通道的输出嘛,就需要32组卷积核 和输入做卷积,所以要乘上32。
因此,用1x1卷积,来改变通道数量,进而降低运算量!看下图,最终得到的结果和上面是一样的,但运算量变成了之前的1/10,计算量小了很多!【这意味着,在训练的时候,用这种方式来减少运算的数量,如之前训练需要10个小时,但现在只需要1个小时!那我们在训练的时候 就可以训练更多的轮数 或者尝试更多的权重!换句话说,省money~】有时候,也把用了1x1的神经网络 叫做 Network in Network——神经网络中的神经网络。
附,对于上图的计算,大家的问题:
[1] 这里的卷积计算,其实不只是针对 1x1的卷积,对所有的卷积都是一样的。卷积核的个数,决定了输出的通道数(或者 反过来也一样,我们自己决定 想要 多少输出通道,这就决定了卷积核的个数)。输入的通道数决定了卷积核的层数。
[2] 变成16是因为 选择用了16个1x1的kernel,想变成其它个数也可以。
Inception的实现:
为了观察,把模型调整一下方向:

卷积计算完毕后,把这四个块儿 拼一起,即 沿着通道的维度把它们拼到一起,因为张量的维度是(batch,channel,width,height)即(b,c,w,g)0 1 2 3,故沿着维度为1 拼起来:(之前,dim=-1就是沿最后一个元素方向)

注意,初始的通道数,这里没有写死,而是初始化的时候,在构造函数里作为参数传进去,目的是将来在实例化的时候 可以指明输入通道数是多少。(更多内容,请看下图的标注)
有同学说:
[1] inception输出的channel一律为88,不改变图像的w,h,只有卷积/池化改变w,h,所以最后88x4x4=1408
附:论文地址
1.10.4 GoogLeNet 练习
网络结构如上目录。
# 昵 称:XieXu
# 时 间: 2023/2/20/0020 12:30
# GoogLeNet练习
import torch
import torch.nn as nn
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim
# prepare dataset
batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))]) # 归一化,均值和方差
train_dataset = datasets.MNIST(root='../dataset/mnist/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist/', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)
# design model using class
class InceptionA(nn.Module):
def __init__(self, in_channels):
super(InceptionA, self).__init__()
self.branch1x1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch5x5_1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch5x5_2 = nn.Conv2d(16, 24, kernel_size=5, padding=2)
self.branch3x3_1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch3x3_2 = nn.Conv2d(16, 24, kernel_size=3, padding=1)
self.branch3x3_3 = nn.Conv2d(24, 24, kernel_size=3, padding=1)
self.branch_pool = nn.Conv2d(in_channels, 24, kernel_size=1)
def forward(self, x):
branch1x1 = self.branch1x1(x)
branch5x5 = self.branch5x5_1(x)
branch5x5 = self.branch5x5_2(branch5x5)
branch3x3 = self.branch3x3_1(x)
branch3x3 = self.branch3x3_2(branch3x3)
branch3x3 = self.branch3x3_3(branch3x3)
branch_pool = F.avg_pool2d(x, kernel_size=3, stride=1, padding=1)
branch_pool = self.branch_pool(branch_pool)
outputs = [branch1x1, branch5x5, branch3x3, branch_pool]
return torch.cat(outputs, dim=1) # b,c,w,h 故c对应的是dim=1
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
self.conv2 = nn.Conv2d(88, 20, kernel_size=5) # 88 = 24x3 + 16
self.incep1 = InceptionA(in_channels=10) # 与conv1 中的10对应
self.incep2 = InceptionA(in_channels=20) # 与conv2 中的20对应
self.mp = nn.MaxPool2d(2)
self.fc = nn.Linear(1408, 10)
def forward(self, x):
in_size = x.size(0)
x = F.relu(self.mp(self.conv1(x)))
x = self.incep1(x)
x = F.relu(self.mp(self.conv2(x)))
x = self.incep2(x)
x = x.view(in_size, -1)
x = self.fc(x)
return x
model = Net()
# construct loss and optimizer
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)
# training cycle forward, backward, update
def train(epoch):
running_loss = 0.0
for batch_idx, data in enumerate(train_loader, 0):
inputs, target = data
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, target)
loss.backward()
optimizer.step()
running_loss += loss.item()
if batch_idx % 300 == 299:
print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
running_loss = 0.0
def test():
correct = 0
total = 0
with torch.no_grad():
for data in test_loader:
images, labels = data
outputs = model(images)
_, predicted = torch.max(outputs.data, dim=1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('accuracy on test set: %d %% ' % (100 * correct / total))
if __name__ == '__main__':
for epoch in range(10):
train(epoch)
test()
我的PC内存不是很大,所以占用会比较多:(ps:散热风扇呼呼转ing…)
1.10.5 GoogLeNet 练习,GPU版
与上一部分几乎一样,只是把model以及运算的部分迁移到GPU来计算:
# 昵 称:XieXu
# 时 间: 2023/2/20/0020 12:54
# GoogLeNet GPU版本
# 网络结构等 都不用动,只是把模型 以及 数据运算 迁移到GPU上
import torch
import torch.nn as nn
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim
# prepare dataset
batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))]) # 归一化,均值和方差
train_dataset = datasets.MNIST(root='../dataset/mnist/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist/', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)
# design model using class
class InceptionA(nn.Module):
def __init__(self, in_channels):
super(InceptionA, self).__init__()
self.branch1x1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch5x5_1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch5x5_2 = nn.Conv2d(16, 24, kernel_size=5, padding=2)
self.branch3x3_1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch3x3_2 = nn.Conv2d(16, 24, kernel_size=3, padding=1)
self.branch3x3_3 = nn.Conv2d(24, 24, kernel_size=3, padding=1)
self.branch_pool = nn.Conv2d(in_channels, 24, kernel_size=1)
def forward(self, x):
branch1x1 = self.branch1x1(x)
branch5x5 = self.branch5x5_1(x)
branch5x5 = self.branch5x5_2(branch5x5)
branch3x3 = self.branch3x3_1(x)
branch3x3 = self.branch3x3_2(branch3x3)
branch3x3 = self.branch3x3_3(branch3x3)
branch_pool = F.avg_pool2d(x, kernel_size=3, stride=1, padding=1)
branch_pool = self.branch_pool(branch_pool)
outputs = [branch1x1, branch5x5, branch3x3, branch_pool]
return torch.cat(outputs, dim=1) # b,c,w,h c对应的是dim=1
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
self.conv2 = nn.Conv2d(88, 20, kernel_size=5) # 88 = 24x3 + 16
self.incep1 = InceptionA(in_channels=10) # 与conv1 中的10对应
self.incep2 = InceptionA(in_channels=20) # 与conv2 中的20对应
self.mp = nn.MaxPool2d(2)
self.fc = nn.Linear(1408, 10)
def forward(self, x):
in_size = x.size(0)
x = F.relu(self.mp(self.conv1(x))) # 卷积和池化的先后关系不影响
x = self.incep1(x)
x = F.relu(self.mp(self.conv2(x)))
x = self.incep2(x)
x = x.view(in_size, -1)
x = self.fc(x)
return x
model = Net()
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu") # 定义device,使用GPU
model.to(device) # 将整个模型运算迁移到GPU
# construct loss and optimizer
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)
# training cycle forward, backward, update
def train(epoch):
running_loss = 0.0
for batch_idx, data in enumerate(train_loader, 0):
inputs, target = data
inputs, target = inputs.to(device), target.to(device) # 张量迁移到GPU 2023.2.20 13:09
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, target)
loss.backward()
optimizer.step()
running_loss += loss.item()
if batch_idx % 300 == 299:
print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
running_loss = 0.0
def test():
correct = 0
total = 0
with torch.no_grad():
for data in test_loader:
images, labels = data
labels, images = labels.to(device), images.to(device) # 迁移到GPU
outputs = model(images)
_, predicted = torch.max(outputs.data, dim=1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('accuracy on test set: %d %% ' % (100 * correct / total))
if __name__ == '__main__':
for epoch in range(10):
train(epoch)
test()
查看GPU调用:

GooLeNet 更强调把网络做得更深,从而使网络变得更为复杂。
----------------------------------分割线----------------------------------
1.10.6 ResNet(残差网络)
ResNet的提出者,来自我国学者何凯明等人。
论文地址:Deep Residual Learning for Image Recognition
一般来讲,并不是训练的轮数越多越好,这期间是有可能出现“过拟合”的,从而错过正确率比较高的点。
如下图,若一直堆叠3x3的卷积,看性能会不会变好。实验发现,就CIFAR数据集来讲,20层的卷积,其性能要比56层的卷积性能更好。

出现 训练轮数多,但效果没有提升反而下降的问题,这可能是由于“梯度消失”了。
由反向传播我们知道,许多梯度相乘,倘若梯度<1的话,那 这么多梯度,会越乘越小,逐渐趋近0。由于权重的训练是 w = w − α × 梯度 w=w-\alpha\times梯度 w=w−α×梯度,那这样对于权重 w w w来讲,就几乎没有改变,训练很多次的效果就微乎其微了。
如何解决这个问题?
1.10.7 Residual Net:“和 x x x做加法”
相比于 在传统神经网络中,先进行权重计算(如卷积,Softmax等),再经过激活函数(如relu等),最终得到输出。
Residual Net 的思想:引入了跳链接,就是 让输入在N(一般 N = 2 N=2 N=2)层连接后并入第N层的输出:
H ( x ) = F ( x ) + x H(x) = F(x) + x H(x)=F(x)+x
然后 再进行ReLU激活,得到输出。
在这样的结构中,以上图为例,如果要进行 H ( x ) H(x) H(x)对 x x x的求导,则会有:
∂ H ( x ) ∂ x = ∂ F ( x ) ∂ x + 1 \frac{\partial H(x)}{\partial x} = \frac{\partial F(x)}{\partial x} + 1 ∂x∂H(x)=∂x∂F(x)+1
也就是说,即便 存在梯度消失现象,即 存在某一层网络中的 ∂ F ( x ) ∂ x → 0 \frac{\partial F(x)}{\partial x} \to 0 ∂x∂F(x)→0,由于上述公式,会使得在反向传播过程中,传播的梯度保持在1左右,即 ∂ H ( x ) ∂ x → 1 \frac{\partial H(x)}{\partial x} \to 1 ∂x∂H(x)→1。那么 离输入较近的层也可以得到充分的训练。
下图中,有同学说:池化是为了减小输入层的尺寸,使得和输出的尺寸一样,才可以跳连接相加。

Residual Block,记得要保证输入张量的维度和输出张量的维度一样。
Residual Block的实现:记得先算 x + y x+y x+y,而后再激活~
1.10.8 Residual Net 练习——accuracy=99%
网络模型及设计如上述介绍。
# 昵 称:XieXu
# 时 间: 2023/2/20/0020 15:00
# ResNet,即 Residual Net。残差网络
import torch
import torch.nn as nn
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim
# prepare dataset
batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))]) # 归一化,均值和方差
train_dataset = datasets.MNIST(root='../dataset/mnist/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist/', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)
# design model using class
class ResidualBlock(nn.Module):
def __init__(self, channels):
super(ResidualBlock, self).__init__()
self.channels = channels
self.conv1 = nn.Conv2d(channels, channels, kernel_size=3, padding=1)
self.conv2 = nn.Conv2d(channels, channels, kernel_size=3, padding=1)
def forward(self, x):
y = F.relu(self.conv1(x))
y = self.conv2(y)
return F.relu(x + y)
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 16, kernel_size=5)
self.conv2 = nn.Conv2d(16, 32, kernel_size=5) # 88 = 24x3 + 16
# self.mp = nn.MaxPool2d(2) # 写这儿也行,写下边也可。。2023.2.20 15:06
self.rblock1 = ResidualBlock(16)
self.rblock2 = ResidualBlock(32)
self.mp = nn.MaxPool2d(2)
self.fc = nn.Linear(512, 10) # 暂时不知道1408咋能自动出来的??? 2023.2.20 15:01
def forward(self, x):
in_size = x.size(0)
x = self.mp(F.relu(self.conv1(x)))
x = self.rblock1(x)
x = self.mp(F.relu(self.conv2(x)))
x = self.rblock2(x)
x = x.view(in_size, -1)
x = self.fc(x)
return x
model