医学图象分割常用损失函数(附Pytorch和Keras代码)
对损失函数没有太大的了解,就是知道它很重要,搜集了一些常用的医学图象分割损失函数,学习一下!
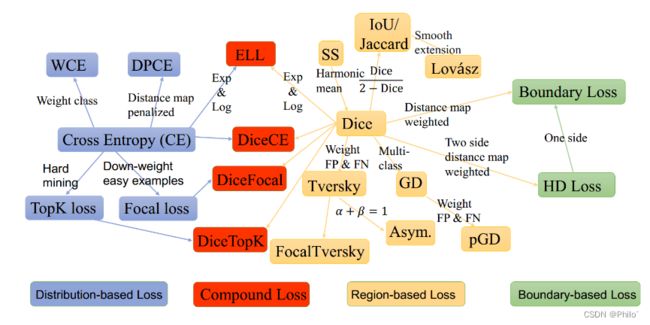
医学图象分割常见损失函数
- 前言
-
- 1 Dice Loss
- 2 BCE-Dice Loss
- 3 Jaccard/Intersection over Union (IoU) Loss
- 4 Focal Loss
- 5 Tvesky Loss
- 6 Focal Tvesky Loss
- 7 Lovasz Hinge Loss
- 8 Combo Loss
- 9 参考资料
前言
分割损失函数大致分为四类,分别是基于分布的损失函数,符合损失函数,基于区域的损失函数以及基于边界的损失函数!
因为有些是评价指标作为损失函数的,因此在反向传播时候,为了使得损失函数趋向为0,需要对类似的损失函数进行1-loss操作!
1 Dice Loss
Dice 系数是像素分割的常用的评价指标,也可以修改为损失函数:
公式:
D i c e = 2 ∣ X ∩ Y ∣ ∣ X ∣ + ∣ Y ∣ Dice=\frac{2|X \cap Y|}{|X|+|Y|} Dice=∣X∣+∣Y∣2∣X∩Y∣
其中X为实际区域,Y为预测区域
Pytorch代码:
import numpy
import torch
import torch.nn as nn
import torch.nn.functional as F
class DiceLoss(nn.Module):
def __init__(self, weight=None, size_average=True):
super(DiceLoss, self).__init__()
def forward(self, inputs, targets, smooth=1):
#comment out if your model contains a sigmoid or equivalent activation layer
inputs = F.sigmoid(inputs)
#flatten label and prediction tensors
inputs = inputs.view(-1)
targets = targets.view(-1)
intersection = (inputs * targets).sum()
dice = (2.*intersection + smooth)/(inputs.sum() + targets.sum() + smooth)
return 1 - dice
import keras
import keras.backend as K
def DiceLoss(targets, inputs, smooth=1e-6):
#flatten label and prediction tensors
inputs = K.flatten(inputs)
targets = K.flatten(targets)
intersection = K.sum(K.dot(targets, inputs))
dice = (2*intersection + smooth) / (K.sum(targets) + K.sum(inputs) + smooth)
return 1 - dice
2 BCE-Dice Loss
这种损失结合了 Dice 损失和标准二元交叉熵 (BCE) 损失,后者通常是分割模型的默认值。将这两种方法结合起来可以使损失具有一定的多样性,同时受益于 BCE 的稳定性。
公式:
D i c e + B C E = 2 ∣ X ∩ Y ∣ ∣ X ∣ + ∣ Y ∣ + 1 N ∑ n = 1 N H ( p n , q n ) Dice + BCE=\frac{2|X \cap Y|}{|X|+|Y|} + \frac{1}{N}\sum_{n=1}^{N}{H(p_n,q_n)} Dice+BCE=∣X∣+∣Y∣2∣X∩Y∣+N1n=1∑NH(pn,qn)
Pytorch代码:
class DiceBCELoss(nn.Module):
def __init__(self, weight=None, size_average=True):
super(DiceBCELoss, self).__init__()
def forward(self, inputs, targets, smooth=1):
#comment out if your model contains a sigmoid or equivalent activation layer
inputs = F.sigmoid(inputs)
#flatten label and prediction tensors
inputs = inputs.view(-1)
targets = targets.view(-1)
intersection = (inputs * targets).sum()
dice_loss = 1 - (2.*intersection + smooth)/(inputs.sum() + targets.sum() + smooth) # 注意这里已经使用1-dice
BCE = F.binary_cross_entropy(inputs, targets, reduction='mean')
Dice_BCE = BCE + dice_loss
return Dice_BCE
Keras代码:
def DiceBCELoss(targets, inputs, smooth=1e-6):
#flatten label and prediction tensors
inputs = K.flatten(inputs)
targets = K.flatten(targets)
BCE = binary_crossentropy(targets, inputs)
intersection = K.sum(K.dot(targets, inputs))
dice_loss = 1 - (2*intersection + smooth) / (K.sum(targets) + K.sum(inputs) + smooth)
Dice_BCE = BCE + dice_loss
return Dice_BCE
3 Jaccard/Intersection over Union (IoU) Loss
IoU 指标,或 Jaccard 指数,类似于 Dice 指标,计算为两个集合之间正实例的重叠与其相互组合值之间的比率;与 Dice 指标一样,它是评估像素分割模型的性能。
公式:
J ( A , B ) = ∣ A ∩ B ∣ ∣ A ∪ B ∣ = ∣ A ∩ B ∣ ∣ A ∣ + ∣ B ∣ − ∣ A ∩ B ∣ J(A,B)=\frac{|A \cap B|}{|A \cup B|} = \frac{|A \cap B|}{|A| + |B|-|A\cap B|} J(A,B)=∣A∪B∣∣A∩B∣=∣A∣+∣B∣−∣A∩B∣∣A∩B∣
其中A为实际分割区域,B为预测的分割区域
Pytorch代码:
class IoULoss(nn.Module):
def __init__(self, weight=None, size_average=True):
super(IoULoss, self).__init__()
def forward(self, inputs, targets, smooth=1):
#comment out if your model contains a sigmoid or equivalent activation layer
inputs = F.sigmoid(inputs)
#flatten label and prediction tensors
inputs = inputs.view(-1)
targets = targets.view(-1)
#intersection is equivalent to True Positive count
#union is the mutually inclusive area of all labels & predictions
intersection = (inputs * targets).sum()
total = (inputs + targets).sum()
union = total - intersection
IoU = (intersection + smooth)/(union + smooth)
return 1 - IoU
Keras代码:
def IoULoss(targets, inputs, smooth=1e-6):
#flatten label and prediction tensors
inputs = K.flatten(inputs)
targets = K.flatten(targets)
intersection = K.sum(K.dot(targets, inputs))
total = K.sum(targets) + K.sum(inputs)
union = total - intersection
IoU = (intersection + smooth) / (union + smooth)
return 1 - IoU
4 Focal Loss
Focal损失函数是由Facebook AI Research的Lin等人在2017年提出的,作为一种对抗极端不平衡数据集的手段。
公式:
见文章:Focal Loss for Dense Object Detection

Pytorch代码:
class FocalLoss(nn.Module):
def __init__(self, weight=None, size_average=True):
super(FocalLoss, self).__init__()
def forward(self, inputs, targets, alpha=0.8, gamma=2, smooth=1):
#comment out if your model contains a sigmoid or equivalent activation layer
inputs = F.sigmoid(inputs)
#flatten label and prediction tensors
inputs = inputs.view(-1)
targets = targets.view(-1)
#first compute binary cross-entropy
BCE = F.binary_cross_entropy(inputs, targets, reduction='mean')
BCE_EXP = torch.exp(-BCE)
focal_loss = alpha * (1-BCE_EXP)**gamma * BCE
return focal_loss
Keras代码:
def FocalLoss(targets, inputs, alpha=0.8, gamma=2):
inputs = K.flatten(inputs)
targets = K.flatten(targets)
BCE = K.binary_crossentropy(targets, inputs)
BCE_EXP = K.exp(-BCE)
focal_loss = K.mean(alpha * K.pow((1-BCE_EXP), gamma) * BCE)
return focal_loss
5 Tvesky Loss
公式:
见文章:Tversky loss function for image segmentation using 3D fully convolutional deep networks

通过公式可以看出,其就是针对不同的指标进行加权,文章中指出,当a = b = 0.5, 就是Dice系数,当a = b = 1,就是Iou系数
Pytorch代码:
class TverskyLoss(nn.Module):
def __init__(self, weight=None, size_average=True):
super(TverskyLoss, self).__init__()
def forward(self, inputs, targets, smooth=1, alpha=0.5, beta=0.5):
#comment out if your model contains a sigmoid or equivalent activation layer
inputs = F.sigmoid(inputs)
#flatten label and prediction tensors
inputs = inputs.view(-1)
targets = targets.view(-1)
#True Positives, False Positives & False Negatives
TP = (inputs * targets).sum()
FP = ((1-targets) * inputs).sum()
FN = (targets * (1-inputs)).sum()
Tversky = (TP + smooth) / (TP + alpha*FP + beta*FN + smooth)
return 1 - Tversky
Keras代码:
def TverskyLoss(targets, inputs, alpha=0.5, beta=0.5, smooth=1e-6):
#flatten label and prediction tensors
inputs = K.flatten(inputs)
targets = K.flatten(targets)
#True Positives, False Positives & False Negatives
TP = K.sum((inputs * targets))
FP = K.sum(((1-targets) * inputs))
FN = K.sum((targets * (1-inputs)))
Tversky = (TP + smooth) / (TP + alpha*FP + beta*FN + smooth)
return 1 - Tversky
6 Focal Tvesky Loss
就是将Focal Loss集成到Tvesky中
公式:
F o c a l T v e r s k y = ( 1 − T v e r s k y ) α FocalTversky = (1-Tversky)^{\alpha } FocalTversky=(1−Tversky)α
Pytorch代码:
class FocalTverskyLoss(nn.Module):
def __init__(self, weight=None, size_average=True):
super(FocalTverskyLoss, self).__init__()
def forward(self, inputs, targets, smooth=1, alpha=0.5, beta=0.5, gamma=2):
#comment out if your model contains a sigmoid or equivalent activation layer
inputs = F.sigmoid(inputs)
#flatten label and prediction tensors
inputs = inputs.view(-1)
targets = targets.view(-1)
#True Positives, False Positives & False Negatives
TP = (inputs * targets).sum()
FP = ((1-targets) * inputs).sum()
FN = (targets * (1-inputs)).sum()
Tversky = (TP + smooth) / (TP + alpha*FP + beta*FN + smooth)
FocalTversky = (1 - Tversky)**gamma
return FocalTversky
Keras代码:
def FocalTverskyLoss(targets, inputs, alpha=0.5, beta=0.5, gamma=2, smooth=1e-6):
#flatten label and prediction tensors
inputs = K.flatten(inputs)
targets = K.flatten(targets)
#True Positives, False Positives & False Negatives
TP = K.sum((inputs * targets))
FP = K.sum(((1-targets) * inputs))
FN = K.sum((targets * (1-inputs)))
Tversky = (TP + smooth) / (TP + alpha*FP + beta*FN + smooth)
FocalTversky = K.pow((1 - Tversky), gamma)
return FocalTversky
7 Lovasz Hinge Loss
该损失函数是由Berman, Triki和Blaschko在他们的论文“The Lovasz-Softmax loss: A tractable surrogate for the optimization of the intersection-over-union measure in neural networks”中介绍的。
它被设计用于优化语义分割的交集优于联合分数,特别是对于多类实例。具体来说,它根据误差对预测进行排序,然后累积计算每个误差对IoU分数的影响。然后,这个梯度向量与初始误差向量相乘,以最强烈地惩罚降低IoU分数最多的预测。
代码连接::
Pytorch代码:https://github.com/bermanmaxim/LovaszSoftmax/blob/master/pytorch/lovasz_losses.py
"""
Lovasz-Softmax and Jaccard hinge loss in PyTorch
Maxim Berman 2018 ESAT-PSI KU Leuven (MIT License)
"""
from __future__ import print_function, division
import torch
from torch.autograd import Variable
import torch.nn.functional as F
import numpy as np
try:
from itertools import ifilterfalse
except ImportError: # py3k
from itertools import filterfalse as ifilterfalse
def lovasz_grad(gt_sorted):
"""
Computes gradient of the Lovasz extension w.r.t sorted errors
See Alg. 1 in paper
"""
p = len(gt_sorted)
gts = gt_sorted.sum()
intersection = gts - gt_sorted.float().cumsum(0)
union = gts + (1 - gt_sorted).float().cumsum(0)
jaccard = 1. - intersection / union
if p > 1: # cover 1-pixel case
jaccard[1:p] = jaccard[1:p] - jaccard[0:-1]
return jaccard
def iou_binary(preds, labels, EMPTY=1., ignore=None, per_image=True):
"""
IoU for foreground class
binary: 1 foreground, 0 background
"""
if not per_image:
preds, labels = (preds,), (labels,)
ious = []
for pred, label in zip(preds, labels):
intersection = ((label == 1) & (pred == 1)).sum()
union = ((label == 1) | ((pred == 1) & (label != ignore))).sum()
if not union:
iou = EMPTY
else:
iou = float(intersection) / float(union)
ious.append(iou)
iou = mean(ious) # mean accross images if per_image
return 100 * iou
def iou(preds, labels, C, EMPTY=1., ignore=None, per_image=False):
"""
Array of IoU for each (non ignored) class
"""
if not per_image:
preds, labels = (preds,), (labels,)
ious = []
for pred, label in zip(preds, labels):
iou = []
for i in range(C):
if i != ignore: # The ignored label is sometimes among predicted classes (ENet - CityScapes)
intersection = ((label == i) & (pred == i)).sum()
union = ((label == i) | ((pred == i) & (label != ignore))).sum()
if not union:
iou.append(EMPTY)
else:
iou.append(float(intersection) / float(union))
ious.append(iou)
ious = [mean(iou) for iou in zip(*ious)] # mean accross images if per_image
return 100 * np.array(ious)
# --------------------------- BINARY LOSSES ---------------------------
def lovasz_hinge(logits, labels, per_image=True, ignore=None):
"""
Binary Lovasz hinge loss
logits: [B, H, W] Variable, logits at each pixel (between -\infty and +\infty)
labels: [B, H, W] Tensor, binary ground truth masks (0 or 1)
per_image: compute the loss per image instead of per batch
ignore: void class id
"""
if per_image:
loss = mean(lovasz_hinge_flat(*flatten_binary_scores(log.unsqueeze(0), lab.unsqueeze(0), ignore))
for log, lab in zip(logits, labels))
else:
loss = lovasz_hinge_flat(*flatten_binary_scores(logits, labels, ignore))
return loss
def lovasz_hinge_flat(logits, labels):
"""
Binary Lovasz hinge loss
logits: [P] Variable, logits at each prediction (between -\infty and +\infty)
labels: [P] Tensor, binary ground truth labels (0 or 1)
ignore: label to ignore
"""
if len(labels) == 0:
# only void pixels, the gradients should be 0
return logits.sum() * 0.
signs = 2. * labels.float() - 1.
errors = (1. - logits * Variable(signs))
errors_sorted, perm = torch.sort(errors, dim=0, descending=True)
perm = perm.data
gt_sorted = labels[perm]
grad = lovasz_grad(gt_sorted)
loss = torch.dot(F.relu(errors_sorted), Variable(grad))
return loss
def flatten_binary_scores(scores, labels, ignore=None):
"""
Flattens predictions in the batch (binary case)
Remove labels equal to 'ignore'
"""
scores = scores.view(-1)
labels = labels.view(-1)
if ignore is None:
return scores, labels
valid = (labels != ignore)
vscores = scores[valid]
vlabels = labels[valid]
return vscores, vlabels
class StableBCELoss(torch.nn.modules.Module):
def __init__(self):
super(StableBCELoss, self).__init__()
def forward(self, input, target):
neg_abs = - input.abs()
loss = input.clamp(min=0) - input * target + (1 + neg_abs.exp()).log()
return loss.mean()
def binary_xloss(logits, labels, ignore=None):
"""
Binary Cross entropy loss
logits: [B, H, W] Variable, logits at each pixel (between -\infty and +\infty)
labels: [B, H, W] Tensor, binary ground truth masks (0 or 1)
ignore: void class id
"""
logits, labels = flatten_binary_scores(logits, labels, ignore)
loss = StableBCELoss()(logits, Variable(labels.float()))
return loss
# --------------------------- MULTICLASS LOSSES ---------------------------
def lovasz_softmax(probas, labels, classes='present', per_image=False, ignore=None):
"""
Multi-class Lovasz-Softmax loss
probas: [B, C, H, W] Variable, class probabilities at each prediction (between 0 and 1).
Interpreted as binary (sigmoid) output with outputs of size [B, H, W].
labels: [B, H, W] Tensor, ground truth labels (between 0 and C - 1)
classes: 'all' for all, 'present' for classes present in labels, or a list of classes to average.
per_image: compute the loss per image instead of per batch
ignore: void class labels
"""
if per_image:
loss = mean(lovasz_softmax_flat(*flatten_probas(prob.unsqueeze(0), lab.unsqueeze(0), ignore), classes=classes)
for prob, lab in zip(probas, labels))
else:
loss = lovasz_softmax_flat(*flatten_probas(probas, labels, ignore), classes=classes)
return loss
def lovasz_softmax_flat(probas, labels, classes='present'):
"""
Multi-class Lovasz-Softmax loss
probas: [P, C] Variable, class probabilities at each prediction (between 0 and 1)
labels: [P] Tensor, ground truth labels (between 0 and C - 1)
classes: 'all' for all, 'present' for classes present in labels, or a list of classes to average.
"""
if probas.numel() == 0:
# only void pixels, the gradients should be 0
return probas * 0.
C = probas.size(1)
losses = []
class_to_sum = list(range(C)) if classes in ['all', 'present'] else classes
for c in class_to_sum:
fg = (labels == c).float() # foreground for class c
if (classes is 'present' and fg.sum() == 0):
continue
if C == 1:
if len(classes) > 1:
raise ValueError('Sigmoid output possible only with 1 class')
class_pred = probas[:, 0]
else:
class_pred = probas[:, c]
errors = (Variable(fg) - class_pred).abs()
errors_sorted, perm = torch.sort(errors, 0, descending=True)
perm = perm.data
fg_sorted = fg[perm]
losses.append(torch.dot(errors_sorted, Variable(lovasz_grad(fg_sorted))))
return mean(losses)
def flatten_probas(probas, labels, ignore=None):
"""
Flattens predictions in the batch
"""
if probas.dim() == 3:
# assumes output of a sigmoid layer
B, H, W = probas.size()
probas = probas.view(B, 1, H, W)
B, C, H, W = probas.size()
probas = probas.permute(0, 2, 3, 1).contiguous().view(-1, C) # B * H * W, C = P, C
labels = labels.view(-1)
if ignore is None:
return probas, labels
valid = (labels != ignore)
vprobas = probas[valid.nonzero().squeeze()]
vlabels = labels[valid]
return vprobas, vlabels
def xloss(logits, labels, ignore=None):
"""
Cross entropy loss
"""
return F.cross_entropy(logits, Variable(labels), ignore_index=255)
# --------------------------- HELPER FUNCTIONS ---------------------------
def isnan(x):
return x != x
def mean(l, ignore_nan=False, empty=0):
"""
nanmean compatible with generators.
"""
l = iter(l)
if ignore_nan:
l = ifilterfalse(isnan, l)
try:
n = 1
acc = next(l)
except StopIteration:
if empty == 'raise':
raise ValueError('Empty mean')
return empty
for n, v in enumerate(l, 2):
acc += v
if n == 1:
return acc
return acc / n
8 Combo Loss
该损失函数是由Taghanaki等人在他们的论文"Combo loss: Handling input and output imbalance in multi-organ segmentation"中介绍的。组合损失是Dice损失和一个修正的BCE函数的组合,像Tversky损失一样,有额外的常数,分别惩罚假阳性或假阴性。
下面这个代码可能有些问题!!
Pytorch代码:
import torch.nn as nn
import torch
ALPHA = 0.5 # < 0.5 penalises FP more, > 0.5 penalises FN more
CE_RATIO = 0.5 #weighted contribution of modified CE loss compared to Dice loss
BETA = 0.5
import torch.nn.functional as F
class ComboLoss(nn.Module):
def __init__(self, weight=None, size_average=True):
super(ComboLoss, self).__init__()
def forward(self, inputs, targets, smooth=1, alpha=ALPHA, beta=BETA, eps=1e-9):
inputs = F.sigmoid(inputs)
#flatten label and prediction tensors
inputs = inputs.view(-1)
targets = targets.view(-1)
#True Positives, False Positives & False Negatives
intersection = (inputs * targets).sum()
dice = (2. * intersection + smooth) / (inputs.sum() + targets.sum() + smooth)
inputs = torch.clamp(inputs, eps, 1.0 - eps)
out = - (ALPHA * ((targets * torch.log(inputs)) + ((1 - ALPHA) * (1.0 - targets) * torch.log(1.0 - inputs))))
weighted_ce = out.mean(-1)
combo = (CE_RATIO * weighted_ce) - ((1 - CE_RATIO) * dice)
return -combo
9 参考资料
医学图象分割常见评价指标
SegLoss
Kaggle比较——SegLoss