自然语言处理(3)——形式语言与自动机
NLP学习笔记(3)——形式语言与自动机
- 1.形式语言
-
- (1)语言
- (2)形式语言
-
- 形式语言
- 形式语法
- 关于推导
- 2. 有限自动机与正则文法
-
- (1)确定的有限自动机
- (3)确定的有限自动机和不确定的有限自动机的区别
- (4)确定的有限自动机和不确定的有限自动机的关系
- (5)正则文法与有限自动机的关系
- 3 有限自动机在NLP中的应用
- 4 课后习题
1.形式语言
(1)语言
- 语言可以了解为一个抽象的数学系统,是按照一定的规律构成的句子和符号串的有限或无限的集合
- ==语言描述的三种途径 ==
(1)穷举法:只适合句子数目有限的语言
(2)语法描述:生成语言中合格的句子
(3)自动机:对输入的句子进行检验,区别哪些是语言中的句子,哪些不是语言中的句子
(2)形式语言
形式语言
- 直观意义(定义):形式语言是用来精确地描述语言(包括人工语言和自然语言)及其结构的手段。
- 形式语言学,也称为代数语言学。
- 形式语言以重写规则 α→β的形式表示,其中α与β均为字符串。一个初步的字符串通过不同的顺序,不断应用不同的重写规则,可以得到不同的新字符串。
形式语法
形式语法是一个4元组G=(N,sigma,P,S)。
其中N为非终结符的有限集合,或者说叫做变量集或语法种类集;
sigma是终结符的有限集合,且有N∩sigma=∅;
V=N∪sigma称为总词汇表;
P是一组重写规则的有限集合:P={α→β},其中均为V中元素构成的字符串,且α中至少应该含有一个非终结符号;
S∈N,称为句子符或者初始符。
关于推导
(1)推导的定义

传递闭包:

自反和传递闭包:

当确定或者默认某个推导是由文法G所产生的,则推导符号下方的G可以省略不写。
(2)最左推导、最右(规范)推导
最左推导:约定每步推导中只改写最左边的那个非终结符。
最右推导(规范推导):约定每步推导只改写最右边的那个非终结符。
文法G的不含非终结符的句子形式成为G生成的句子。
由文法G生成的语言,记做L(G),指G生成的所有句子的集合,即有
L ( G ) = { x ∣ x ∈ ∑ , S ⇒ ∗ x } L(G)=\{x|x\in \sum,S \overset{*}\Rightarrow x \} L(G)={x∣x∈∑,S⇒∗x}
(4)关于正则文法(3型文法)
左线性正则文法称为3型文法
关于正则文法,如果文法G=(N,sigma,P,S)的P,其中的规则满足如下的形式:A→Bx,或A→x,其中A,B∈N,x∈sigma,则称该文法为正则文法或3型文法(左线性正则文法);
满足A→xB,则称该文法为右线性正则文法。
(5)上下文无关文法(2型文法)——上下文有关文法的特例
context-free grammar(CFG)
如果P中的规则满足如下形式:A→α,其中A属于N,α属于(N∪sigma)*,则称该文法为上下文无关文法,或称2型文法。
一个栗子:

(6)上下文有关文法(1型文法)
context-sensitive grammar,CSG
如果P中的规则满足如下形式:αAβ→αγβ,其中A∈N,α,β,γ∈(N∪sigma)*,且γ中至少包含一个字符(A直接消去的情况不予记录),则称该文法为上下文有关文法,或1型文法。
当α和β均为空时,上下文有关文法转化为上下文无关文法,无关文法是有关文法的特例。
或者定义为如下形式:

一个栗子:

(7)无约束文法(0型文法、无限制重写系统)
如果P中的规则满足如下形式:α→β,α,β是字符串,则称G为无约束文法,或称为0型文法。
如果一种语言能由几种文法产生,则把这种语言称为在这几种文法中受限制最多的那种文法所产生的的语言。
(8)上下文无关文法产生的语言句子的派生树表示的步骤:
CFG
G = (N,sigma,P,S)
- 对于任意x∈N∪sigma,给一个标记作为节点,S作为树的根节点。
- 如果一个节点的标记为A,并且它至少有一个除他自身之外的后裔,则A∈N。
- 如果一个节点的标记为A,它的k(k>0)个直接后裔节点按照从左到右的次序一次标记为A1,A2,A3……Ak,则有A→A1A2……Ak一定是P中的一个产生式。
派生树又称语法树、分析树、推导树
一个栗子:

(9)上下文无关文法的二义性
一个文法G,如果存在某个句子有不只一棵分析树与之对应,则称这个文法是二义的。




2. 有限自动机与正则文法
(1)确定的有限自动机
(3)确定的有限自动机和不确定的有限自动机的区别
(4)确定的有限自动机和不确定的有限自动机的关系
(5)正则文法与有限自动机的关系
3 有限自动机在NLP中的应用
(1)在NLP中,英语单词的拼写检查:
设X为拼写错误的字符串,长度为m,Y为X对应的GT,长度为n。则X与Y 的编辑距离ed(X[m],Y[n])定义为:
从字符串X转换到Y所需要的插入、删除、替换和交换两个相邻的基本单位字符的最小个数。






(2)对于有限状态机
构造一个确定的有限状态机R,有定义R=(Q,A,δ,q0,F)
其中Q表示状态集,A表示输入字符集,δ为QxA→Q的一个函数,q0∈Q,为起始状态,F包含于Q为终止状态集。
当L包含于A*表示有限状态机R接收的语言,字母构成的所有合法单词都是有限状态机中的一条路径。当给定一个输入 串,对其进行检查的过程就是在给定阈值t(>0)的情况下,寻找那些与输入串的编辑距离小于t的路径。则一个字符串X[m]∉L能够被R识别的条件是存在一个非空集合C:

即存在一条L中存在的已知路径,该路径与X间的路径距离不大于t
(3)单词拼写检查
一般,英文单词可以使用键树(数字查找树)来存储。
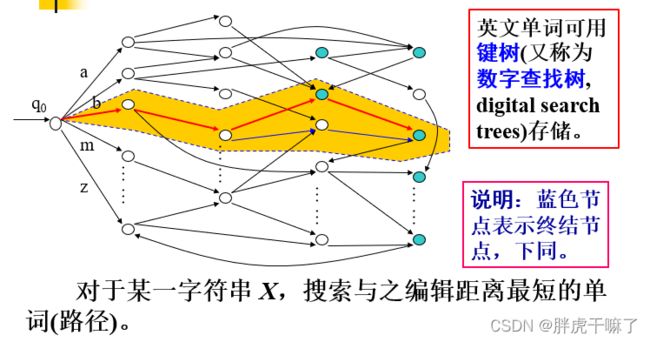

关于为何使用t作为变量,编辑距离中X长度的取值范围:
若X的长度小于n-t,则X需要至少t+1次的增加操作才能达到与字符串Y相同;
若X的长度大于n+t,则X至少需要t+1次的删除操作才能达到与字符串Y相同。
仔细观察上图,关于阈值t,并非X与Y长度差的二分之一,而是我们前文中提到的,事先设定的阈值
由此有了上图右下角的说明:
关于阈值t的作用:是为了确定截取X的范围;进一步地,也能限制编辑距离(有可能小于阈值长度t)。
一个栗子:

(4)关于采用深度优先搜索算法从自动机中选择路径:




(5)关于使用有限自动机进行英语单词形态分析
Note:在实际的应用中,除了有限状态机,还常常使用有限状态转换机(Finite State Transducer,FST)的概念。
粗略的讲,有限状态转换机与有限自动机(有限状态机)的区别:
有限状态转换机FST在完成状态转移的同时产生一个输出。而有限自动机FA或有限状态机FSM只实现状态的转移,而不产生任何输出。
可以观察到,在上述的状态转换过程中,有限状态转换机在状态转移的过程中,还产生了字符的输出。
4 课后习题
L ( G ) = a t + 1 ⋅ b t + 1 ⋅ c t + 1 L(G) = a^{t+1}·b^{t+1}·c^{t+1} L(G)=at+1⋅bt+1⋅ct+1





















