基于梯度的优化问题中不可导操作的处理方法总结

1 引言

一些不可导的场景：

• 深度学习中大规模参数的优化方法都是基于梯度的，因此要求模型中的操作都是可导的。然而机器学习模型中经常存在非全空间可导的函数或操作，比如常用的ReLU激活函数、argmax操作、卷积中的Max Pooling操作等。
• 许多机器学习任务的评价指标是离散的，如分类任务的评价指标是准确率；而常见的损失函数是连续的，如分类任务使用交叉熵损失。损失函数的降低和评价指标的提升并不是完全的单调关系，但不能直接使用评价指标作为损失函数，因为评价指标是不可导的。
• 在强化学习任务中，假设网络输出的三维向量的分量代表三个动作（比如前进、停留、后退）在下一步的收益，那么下一步我们就会选择收益最大的动作继续执行。选择收益最大的动作作为输出动作，在神经网络中这种取法有个问题是不能计算梯度，也就不能更新网络。
• 在最优化问题中，求函数极值需要求导，有时目标函数是不可导的，比如函数中存在最大值函数$max(x)$，希望将这些不可导函数用可导函数近似。

基于以上场景，需要寻求对不可导函数近似为可导函数的方法或者其梯度的近似方法。

2 函数光滑化的方法

2.1 概念定义

光滑函数(smooth function)是指在其定义域内无穷阶数连续可导的函数。

函数的光滑化是指对于一个非光滑函数$f$，寻找一个光滑函数$f_{\mu }$, 使得$f_{\mu }$是$f$的光滑逼近。一个非光滑函数是否可光滑化(smoothable)定义如下：
给定一个凸函数$f$，如果存在一个凸函数$f_{\mu }$，使得满足：
(1) $f_{\mu }$是$\frac{\alpha }{\mu }$光滑的；
(2) $f_{\mu }(x)\le f(x)\le f_{\mu }+\beta \mu$；
我们称其为$(\alpha ,\beta )-\text{smoothable}$，并且称$f_{\mu }$为$f$在参数$(\alpha ,\beta )$下的$\frac{1}{\mu }$光滑逼近。
条件(1)要求$f_{\mu }$是光滑的，并指定光滑系数$\frac{\alpha }{\mu }$（越小越光滑）。条件(2)要求$f_{\mu }$从下方逼近$f$,并且制定逼近的最大差异$\beta \mu$。参数$\mu$越大，则函数$f_{\mu }$越光滑，但与$f$的差异也就越大。

2.2 人工选取光滑近似

2.2.1 $max(x_1,x_2,...,x_n)\approx \ln ({\sum }_{i=1}^n{e}^{x_i})$

推导过程
以max(x, y)为例。
当$x\ge 0,y\ge 0$时，有最大值函数的近似公式：
$$\max (x,y)=\frac{1}{2}(|x+y|+|x-y|)$$
因此问题转化为寻找绝对值函数$f(x)=|x|$的光滑近似，该函数可以的导数可以用单位阶跃函数$\theta (x)$表示，即：
$$f^{\prime }(x)=2\theta (x)-1$$
单位阶跃函数$\theta (x)$具有近似函数$\theta (x)={\lim }_{k\to \infty }\frac{1}{1+e^{-kx}}$,因此：
$$\begin{array}{rl}f(x)& =\int [2\theta (x)-1]dx\\ & =\int [2\frac{1}{1+e^{-kx}}-1]dx\\ & =\frac{2}{k}\ln (1+e^{kx})-x\\ & =\frac{2}{k}\ln (1+e^{kx})-\frac{2}{k}\ln e^{\frac{kx}{2}}\\ & =\frac{1}{k}\ln (e^{kx}+e^{-kx}+2)\end{array}$$
当k足够大时，常数2可以省略。因此$|x|={\lim }_{k\to \infty }\frac{1}{k}\ln (e^{kx}+e^{-kx})$，进一步推得：
$$\begin{array}{rl}\max (x,y)& =\frac{1}{2}(|x+y|+|x-y|)\\ & =\underset{k\to \infty }{\lim }\frac{1}{2k}\ln (e^{2kx}+e^{2ky}+e^{-2kx}+e^{-2ky})\\ & =\underset{k\to \infty }{\lim }\frac{1}{k}\ln (e^{kx}+e^{ky}+e^{-kx}+e^{-ky})\end{array}$$
注意前提条件时$x\ge 0,y\ge 0$，因此$e^{-kx}+e^{-ky}$可丢弃。最终max函数近似为：
$$\max (x,y)=\underset{k\to \infty }{\lim }\frac{1}{k}\ln (e^{kx}+e^{ky})$$
注意该式子在x,y取负数时仍成立，因此可以推广到多个变量的最大值函数：
$$\max (x_1,x_2,...,x_n)=\underset{k\to \infty }{\lim }\frac{1}{k}\ln (\sum _{i=1}^n{e}^{k{x}_i})$$
通常设置k=1, 则有：
$$\max (x_1,x_2,...,x_n)\approx \ln (\sum _{i=1}^n{e}^{k{x}_i})$$

2.2.2 $onehot(\mathrm{argmax}(x_1,x_2,...,x_n))\approx softmax(x_1,x_2,...,x_n)$

推导过程
$onehot(argmax(x))$表示求序列$x=[x_1,x_2,...,x_n]$中最大值所在的位置的onehot编码。考虑向量：
$$x^{\prime }=[x_1,x_2,...,x_n]-\max (x_1,x_2,...,x_n)$$
其最大值对应的位置值为0，其余位置值为负数，继而考虑
$$e^{x^{\prime }}=[e^{x_1-\max (x_1,x_2,...,x_n)},e^{x_2-\max (x_1,x_2,...,x_n)},...,e^{x_n-\max (x_1,x_2,...,x_n)}]$$
作为$onehot(\mathrm{argmax}(x_1,x_2,...,x_n))$的近似。上式最大值处取值为$e^0=1$，其余值处接近0。根据前述结论$max(x_1,x_2,...,x_n)\approx \ln ({\sum }_{i=1}^n{e}^{x_i})$，有：
$$\begin{array}{rl}onehot(\mathrm{argmax}(x_1,x_2,...,x_n))& \approx e^{x^{\prime }}\\ & =[e^{x_1-\max (x_1,x_2,...,x_n)},e^{x_2-\max (x_1,x_2,...,x_n)},...,e^{x_n-\max (x_1,x_2,...,x_n)}]\\ & =[e^{x_1-\ln ({\sum }_{i=1}^n{e}^{x_i})},e^{x_2-\ln ({\sum }_{i=1}^n{e}^{x_i})},...,e^{x_n-\ln ({\sum }_{i=1}^n{e}^{x_i})}]\\ & =[\frac{e^{x_1}}{{\sum }_{i=1}^n{e}^{x_i}},\frac{e^{x_2}}{{\sum }_{i=1}^n{e}^{x_i}},...,\frac{e^{x_n}}{{\sum }_{i=1}^n{e}^{x_i}}]\\ & =softmax(x_1,x_2,...,x_n)\end{array}$$

2.2.3 $argmax(x)\approx {\sum }_{i=1}^{n}i\times softmax(x{)}_i$

推导过程
$argmax(x)$表示求序列$x=[x_1,x_2,...,x_n]$中最大值所在的位置，注意到$argmax(x)$实际上等于如下內积：
$$\text{向量}[1,2,...,n]\cdot onehot(\mathrm{argmax}(x))$$
根据前述结论$onehot(\mathrm{argmax}(x_1,x_2,...,x_n))\approx softmax(x_1,x_2,...,x_n)$，可得：
$$\begin{array}{rl}argmax(x)& \approx \sum _{i=1}^{n}i\times \text{softmax}(x{)}_i\\ & =\sum _{i=1}^{n}i\times \frac{e^{x_i}}{{\sum }_{j=1}^n{e}^{x_j}}\end{array}$$

2.2.4 $\text{accuracy}\approx \frac{1}{S}{\sum }_{x\in S}<1_y(x),p(x)>$

本节讨论分类任务中正确率$\text{accuracy}$的光滑近似。
推导过程
给定一个批量样本$S$，用$1_y(x)$表示样本的真实类别$y$对应的onehot编码，$1_{y^{{}^{\prime }}}(x)$表示样本的预测类别$y^{{}^{\prime }}$对应的onehot编码。统计两个编码对应的内积之和(预测相同内积为1否则为0)，表示为$<1_y(x),1_{y^{{}^{\prime }}}(x)>$，即可得到正确率的表达式(预测正确的数量占总数量的比值)：
$$accuracy=\frac{1}{S}\sum _{x\in S}<1_y(x),1_{y^{{}^{\prime }}}(x)>$$
网络的预测结果$1_{y^{{}^{\prime }}}(x)$是经过softmax的概率分布$p(x)$，则正确率的光滑近似为:
$$accuracy\approx \frac{1}{S}\sum _{x\in S}<1_y(x),p(x)>$$

2.2.5 $\text{F1-score}\approx \frac{2{\sum }_{x\in S}p(x)y(x)}{{\sum }_{x\in S}p(x)+y(x)}$

F1-score是分类问题常用的评估指标，计算为查准率和查全率的调和平均。对于二分类问题，若记$p(x)$是预测正类的概率，$y(x)$是样本的标签，则对应的混淆矩阵如下:

标签\ 预测	正例	反例
正例	$TP\approx p(x)g(x)$	$FN\approx (1-p(x))g(x)$
反例	$FP\approx p(x)(1-g(x))$	$TN\approx (1-p(x))(1-g(x))$

则F1-score计算公式为
$$\text{F1-score}=\frac{2TP}{2TP+FP+FN}\approx \frac{2{\sum }_{x\in S}p(x)y(x)}{{\sum }_{x\in S}p(x)+y(x)}$$
上述推导的F1-score的光滑近似是可导的，可以将其相反数作为损失函数。但是在采样过程中，上式是F1-score的有偏估计。通常应先用交叉熵训练一段时间，再用上式进行微调。

2.3 使用冲激函数近似

参考paper：
SAU: Smooth activation function using convolution with approximate identities
paper解读：https://0809zheng.github.io/2021/11/05/sau.html

3 不可导点的次梯度方法

比如ReLU激活函数f(x)=max(0, x)在x=0处不可导。
次梯度c定义为：
$$c\le \frac{f(x)-f(x_0)}{x-x_0}$$
对于ReLU函数, 当x>0的时候,其导数为1; 当x<0时,其导数为0。 则ReLU函数在x=0的次梯度$c\in [0,1]$，这里是次梯度有多个,可以取0,1之间的任意值. 工程上为了方便取c=0即可。

4 采样的重参数化方法

重参数化的目的是分离随机变量的不确定性，使得原先无法求导或者梯度传播的中间节点可以求导。

4.1 对连续分布采样的重参数化

一般假设连续分布的变量x服从高斯分布，即$x\sim N(\mu ,{\sigma }^2)$，从这个分布中采样是不可导的。欲使其可导，我们可以这样做：首先从均值为0，标准差为1的高斯分布中采样一个值$ϵ$，再放缩平移得到x。
$$x=\mu +\sigma \ast ϵ,ϵ\sim \mathbb{N}(0,1)$$
x的生成只涉及了线性操作(平移缩放),真正的采样操作在神经网络的计算图之外,而$ϵ$对于神经网络来说只是一个常数。

4.2 对离散分布采样的重参数化（Gumbel-softmax）

比如文章开头提到的强化学习中离散动作的采样，就是适合应用这个方法的案例。经典的离散分布采样方法就是用softmax函数加上轮盘赌方法（np.random.choice）：

def sample_with_softmax(logits, size):
# logits为输入数据
# size为采样数
    pro = softmax(logits)
    return np.random.choice(len(logits), size, p=pro)

轮盘赌方法就是多项式采样，这个不解释，请自行搜索了解。
要解决轮盘赌方法不可导问题，可以借助Gumbel分布。让我们一步步推到出Gumbel-softmax方法。
推到过程
对于softmax函数输出n维向量的第i维的分量${\alpha }_i=\frac{e^{x_i}}{{\sum }_{j=1}^n{e}^{x_j}}$，取对应的变换$log({\alpha }_i)$并加上Gumbel噪声，得到新变量${\pi }_i$:
$$\begin{array}{r}{\pi }_i=\underset{i}{\mathrm{argmax}}([log({\alpha }_1)+G_1,log({\alpha }_2)+G_2,log({\alpha }_i)+G_i,...,log({\alpha }_n)+G_n])\end{array}$$
其中，$G_i$是满足标准Gumbel分布的随机变量,即$G_i=-log(-log(U_i))$, $U_i$服从均匀分布$U(0,1)$；

上述公式（16）也称Gumbel-max方法。
可以证明，Gumbel-max 方法的采样效果等效于前述基于“softmax+轮盘赌“的方式(该结论证明可参考：盘点深度学习中的不可导操作(次梯度和重参数化))。由于 Gumbel 随机数可以预先计算好，采样过程也不需要计算 softmax，因此，某些情况下，gumbel-max 方法相比于 softmax，在采样速度上会有优势。当然，可以看到由于这中间有一个argmax操作，这是不可导的，依旧没法用于计算网络梯度。argmax操作的近似为可导的操作只需要参考前文第2.2.3节的近似公式即可，于是变量${\pi }_i$近似处理为:
$$\begin{array}{r}{\pi }_i\approx {\text{softmax}}_i(log({\alpha }_i)+G_i)\end{array}$$
实际应用中通常还会加一个温度变量$\tau$，使${\pi }_i$变为：
$$\begin{array}{r}{\pi }_i\approx {\text{softmax}}_i（\frac{log({\alpha }_i)+G_i}{\tau }）\end{array}$$
$\tau$是大于零的参数，它控制着 softmax 的 soft 程度。温度越高，生成的分布越平滑；温度越低，生成的分布越接近离散的 one-hot 分布。神经网络训练中，可以通过逐渐降低温度，以逐步逼近真实的离散分布。

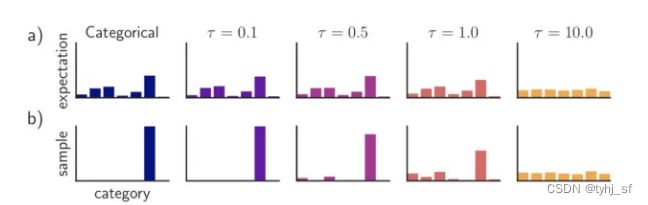
公式（18）即为Gumbel-softmax重参数方法。

5 参考资料

[1]. https://0809zheng.github.io/2021/11/16/mollifier.html
[2]. https://zhuanlan.zhihu.com/p/97465608
[3].The Reparameterization Trick, 2018.4