弱监督实例分割 Box-supervised Instance Segmentation with Level Set Evolution 论文笔记
弱监督实例分割 Box-supervised Instance Segmentation with Level Set Evolution 论文笔记
- 一、Abstract
- 二、引言
- 三、相关工作
-
- 3.1 基于 Box 的实例分割
- 3.2 基于层级的分割
- 四、提出的方法
-
- 4.1 图像分割中的层级模型
- 4.2 基于 Box 的实例分割
-
- 在 Bounding Box 内的层级进化
- 输入的数据格式
- 层级初始化
- 4.3 训练和推理
-
- 损失函数
- 推理
- 五、实验
-
- 5.1 数据集
- 5.2 实施细节
- 5.3 主要结果
- 5.4 消融实验
-
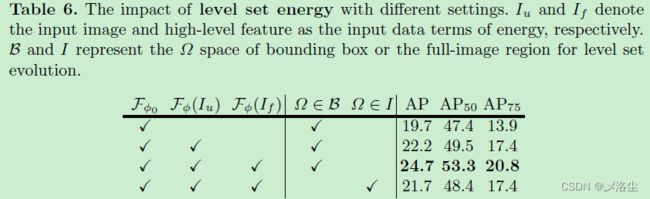
- 层级能量
- 高层特征的通道数量
- 训练计划
- 深度结构特征的有效性
- 六、结论
写在前面
这是一篇基于 Box 的弱监督实例分割文章,之前也分享过几篇(主页有,欢迎关注一下呗~),采用旧纸堆里面翻出来的能量函数来做弱监督。
- 论文地址:Box-supervised Instance Segmentation with Level Set Evolution
- 代码地址:https://github.com/LiWentomng/boxlevelset
- 收录于:ECCV 2022
- 补一下博客篇数,2023年每周一篇,还剩下6篇未补。欢迎关注,长年稳定更新~
一、Abstract
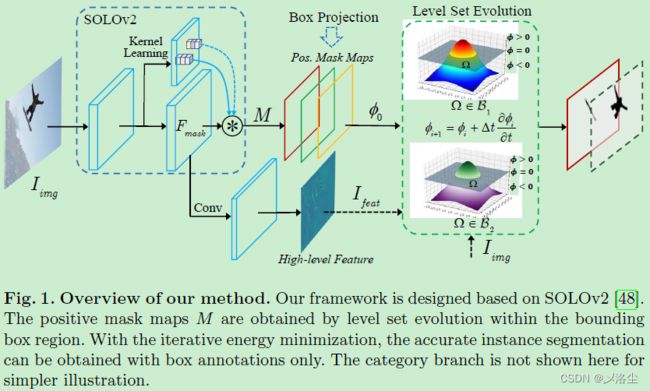
本文提出一种 single-shot 的基于 box 监督的实例分割方法,致力于整合传统的能量函数模型以及深度神经网络。具体来说,以一种端到端的方式,通过一个连续的 Chan-Vese 能量函数来迭代地学习一系列层级(mask?):采用 SLOLv2 来自适应地预测实例感知的 mask 作为每一个实例层级。所有的输入图像及提取的特征都用来进化层级曲线,其中一个 box 投影函数用来获得初始的边界。通过最小化可微分的能量函数,每个实例的层级在其对应的 box 标注框内被迭代地优化,实验结果很牛皮。
二、引言
第一段实例分割的目的,应用,之前方法对于标注的依赖。
第二段介绍现有的基于 Box 的方法,基于伪标签的以及颜色相似度的,即 BBTP 和 Boxinst。本文指出这两种方法过于简化了一个假设:像素或者颜色对被强制共享相同的颜色,于是来自相似形状目标和背景的噪声上下文无可避免地会影响训练,使得性能不太好。
本文提出一种 single-shot 的基于 box 监督的实例分割方法来解决这些问题,致力于整合传统的能量集合模型以及深度神经网络。以一种端到端的方式在标注的 Bounding box 内,从隐藏的曲线卷积中来迭代地学习一系列层级(mask?)。
具体来说,引入一种传统 Chan-Vese 能量函数,并采用 SOLOv2来预测实例感知的mask 图来作为每个实例的层级。除输入的特征图外,还采用了一种长范围依赖的深度结构特征来稳定地进化层级曲线,得以向目标边界逼近。通过最小化可微分的能量函数,每个实例的层级在其对应的 box 标注框内被迭代地优化,实验结果很牛皮。
贡献如下:
- 第一个提出一种基于层级进化的方法用在基于 box 的弱监督实例分割上;
- 将深度结构特征并入低层级的图像,在 bounding box 区域内实现稳定的层级进化,其中一个 box 的投影函数用于层级初始化。
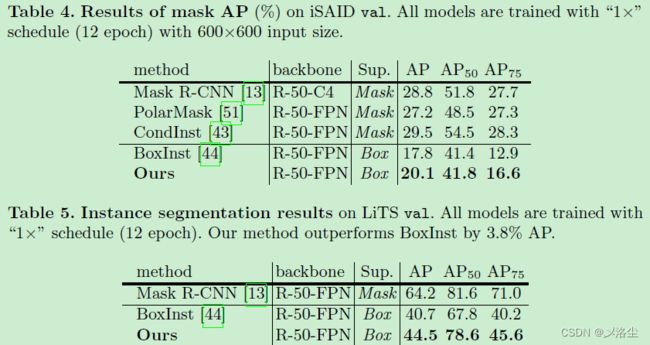
- 在 COCO、PASCAL VOC、遥感数据集 iSAID 和医疗数据集 LiTS上效果很好。
三、相关工作
3.1 基于 Box 的实例分割
讲一下最近的方法,指出 BBTP 和 Boxinst,这两种方法过于简化了一个假设:像素或者颜色对被强制共享相同的颜色,因此来自相似形状目标和背景的噪声上下文无可避免地会影响训练,使得性能不太好。除了这两个外,最近的 BBAM 和 DIscoBox 关注于代理 mask 标签的生成,需要多个阶段的训练或者多个网络结构。而本文提出的基于层级方法以一种端到端的隐含方式通过优化 box 区域内的能量函数来迭代地对齐实例边界。
3.2 基于层级的分割
主要划分为两类:基于区域和边缘的方法。核心理念是在一个高维度通过一个能量函数来展现隐藏的曲线,而这能够用梯度下降来优化。接下来是一些举例,指出他们的不足:全监督方式训练网络去预测不同的子区域并得到目标的边界,而本文提出的是 box 级别的监督。
四、提出的方法
一些符号:输入的图像 I i m g I_{img} Iimg,高层深度特征 I f e a t I_{feat} Ifeat,初始层级 ϕ 0 \phi_0 ϕ0
4.1 图像分割中的层级模型
对层级方法的回顾:将图像分割视为一种连续的能量最小化问题。
Mumford-Shah 层级模型:给定一图像 I I I,找到一组参数化的轮廓 C C C,将图像层级 Ω ∈ R 2 \Omega\in\mathbb{R}^2 Ω∈R2 划分为 N N N 个不联通的区域 Ω 1 , ⋯ , Ω N \Omega_1, \cdots, \Omega_N Ω1,⋯,ΩN。Mumford-Shah 能量函数 F M S \mathcal F^{MS} FMS 定义如下:
F M S ( u 1 , ⋯ , u N , Ω 1 , ⋯ , Ω N ) = ∑ i = 1 N ( ∫ Ω i ( I − u i ) 2 d x d y + μ ∫ Ω i ∣ ∇ u i ∣ 2 d x d y + γ ∣ C i ∣ ) , \mathcal F^{MS}(u_1,\cdots,u_N,\Omega_1,\cdots,\Omega_N)=\sum\limits_{i=1}^{N}(\int\limits_{\Omega_i}(I-u_i)^2dxdy+\mu\int\limits_{\Omega_i}|\nabla u_i|^2dxdy+\gamma|C_i|), FMS(u1,⋯,uN,Ω1,⋯,ΩN)=i=1∑N(Ωi∫(I−ui)2dxdy+μΩi∫∣∇ui∣2dxdy+γ∣Ci∣),其中 u i u_i ui 为接近于输入 I I I 的光滑分段函数,目的是确保每个区域 Ω i \Omega_i Ωi 内的光滑。 μ \mu μ, γ \gamma γ 为加权系数。
之后 Chan 和 Vese 简化了这一能量函数:
F CV ( ϕ , x , c 2 ) = ∫ Q ∣ I ( x , y ) − c 1 ∣ 2 H ( ϕ ( x , y ) ) d x d y + ∫ Q ∣ I ( x , y ) − c 2 ∣ 2 ( 1 − H ( ϕ ( x , y ) ) ) d x d y + γ ∫ Q ∣ ∇ H ( ϕ ( x , y ) ) ∣ d x d y \begin{aligned}\mathcal{F}^{\text{CV}}(\phi,x,c_2)&=\int\limits_{Q}\left|I(x,y)-c_1\right|^2H(\phi(x,y))dxdy\\ &+\int\limits_{Q}\left|I(x,y)-c_2\right|^2(1-H(\phi(x,y)))dxdy+\gamma\int\limits_{Q}\left|\nabla H(\phi(x,y))\right|dxdy\end{aligned} FCV(ϕ,x,c2)=Q∫∣I(x,y)−c1∣2H(ϕ(x,y))dxdy+Q∫∣I(x,y)−c2∣2(1−H(ϕ(x,y)))dxdy+γQ∫∣∇H(ϕ(x,y))∣dxdy其中 H H H 为 Heaviside 海塞函数, ϕ ( x , y ) \phi(x,y) ϕ(x,y) 为层级函数,如果为 0 则表示轮廓 C = { ( x , y ) : ϕ ( x , y ) = 0 } C=\{(x,y):\phi(x,y)=0\} C={(x,y):ϕ(x,y)=0} 将图像空间 Ω \Omega Ω 划为两个不连通区域,内部轮廓为 C : Ω 1 = { ( x , y ) : ϕ ( x , y ) > 0 } C\colon\Omega_1=\{(x,y):\phi(x,y)>0\} C:Ω1={(x,y):ϕ(x,y)>0},外部轮廓为 C : Ω 2 = { ( x , y ) : ϕ ( x , y ) < 0 } C\colon\Omega_2=\{(x,y):\phi(x,y)<0\} C:Ω2={(x,y):ϕ(x,y)<0}。上式右边一二项倾向于拟合数据,第三项用一个非负系数 γ \gamma γ 归一化 0 0 0 层级轮廓。 c 1 c_1 c1, c 2 c_2 c2 分别为 C C C 内部和 C C C 外部的输入 I ( x , y ) I(x,y) I(x,y) 的均值。
于是通过 c 1 c_1 c1 和 c 2 c_2 c2 找到一个层级函数 ϕ ( x , y ) = 0 \phi(x,y)=0 ϕ(x,y)=0 来优化能量函数 F CV \mathcal{F}^{\text{CV}} FCV,从而得到图像的分割结果。
4.2 基于 Box 的实例分割
在 Bounding Box 内的层级进化
给定输入图像 I ( x , y ) I(x,y) I(x,y),旨在标注的 bounding box B \mathcal{B} B 区域内隐式地进化出一组层级来预测目标边界曲线。由 SOLOv2 预测出的尺寸为 H × W H\times W H×W 的 mask M ∈ R H × W × S 2 M\in\mathbb{R}^{H\times W\times S^2} M∈RH×W×S2 包含 S × S S\times S S×S 个可能的实例图。每一个可能的实例图仅包含一个实例,他们的中心位于 ( i , j ) (i,j) (i,j)。位置 ( i , j ) (i,j) (i,j) 处预测出 mask 类别概率 p i , j ∗ > 0 p^{*}_{i,j}>0 pi,j∗>0 时被视为正样本。然后将 box B \mathcal{B} B 内的每个正样本图作为层级 ϕ ( x , y ) \phi(x,y) ϕ(x,y),其输入图像 I ( x , y ) I(x,y) I(x,y) 相应的像素空间被视为 Ω \Omega Ω,即 Ω ∈ B \Omega\in\mathcal{B} Ω∈B。当 C = { ( x , y ) : ϕ ( x , y ) = 0 } C=\{(x,y):\phi(x,y)=0\} C={(x,y):ϕ(x,y)=0} 时,对应的 C C C 为分割出的边界,此时 box 区域被划分为不相连的前景和背景区域。
通过优化下面的能量函数来学习一系列的层级 ϕ ( x , y ) \phi(x,y) ϕ(x,y):
F ( ϕ , I , c 1 , c 2 , B ) = ∫ Ω ∈ B ∣ I ∗ ( x , y ) − c 1 ∣ 2 σ ( ϕ ( x , y ) ) d x d y + ∫ Ω ∈ B ∣ I ∗ ( x , y ) − c 2 ∣ 2 ( 1 − σ ( ϕ ( x , y ) ) ) d x d y + γ ∫ Ω ∈ B ∣ ∇ σ ( ϕ ( x , y ) ) ∣ d x d y \begin{aligned} \mathcal{F}\left(\phi, I, c_{1}, c_{2}, \mathcal{B}\right) & =\int_{\Omega \in \mathcal{B}}\left|I^{*}(x, y)-c_{1}\right|^{2} \sigma(\phi(x, y)) d x d y \\ & +\int_{\Omega \in \mathcal{B}}\left|I^{*}(x, y)-c_{2}\right|^{2}(1-\sigma(\phi(x, y))) d x d y+\gamma \int_{\Omega \in \mathcal{B}}|\nabla \sigma(\phi(x, y))| d x d y \end{aligned} F(ϕ,I,c1,c2,B)=∫Ω∈B∣I∗(x,y)−c1∣2σ(ϕ(x,y))dxdy+∫Ω∈B∣I∗(x,y)−c2∣2(1−σ(ϕ(x,y)))dxdy+γ∫Ω∈B∣∇σ(ϕ(x,y))∣dxdy其中 I ∗ ( x , y ) I^{*}(x,y) I∗(x,y) 表示归一化后的图像 I ( x , y ) I(x,y) I(x,y), γ \gamma γ 为非负系数, σ \sigma σ 为 s i g m o i d sigmoid sigmoid 函数,其被视为层级 ϕ ( x , y ) \phi(x, y) ϕ(x,y) 的特征函数。相比于传统的 Heaviside 海塞函数, s i g m o i d sigmoid sigmoid 更为光滑,能够更好地表示预测实例的特征以及提高层级进化在训练过程中的收敛。上式右边一二项旨在强制预测的 ϕ ( x , y ) \phi(x, y) ϕ(x,y) 统一内部区域 Ω \Omega Ω 和外部区域 Ω ˉ \bar\Omega Ωˉ。 c 1 c_1 c1, c 2 c_2 c2 为 Ω \Omega Ω 和 Ω ˉ \bar\Omega Ωˉ 的均值,定义如下:
c 1 ( ϕ ) = ∫ Ω ∈ B I ∗ ( x , y ) σ ( ϕ ( x , y ) ) d x d y ∫ Ω ∈ B σ ( ϕ ( x , y ) ) d x d y , c 2 ( ϕ ) = ∫ Ω ∈ B I ∗ ( x , y ) ( 1 − σ ( ϕ ( x , y ) ) ) d x d y ∫ Ω ∈ B ( 1 − σ ( ϕ ( x , y ) ) ) d x d y c_1(\phi)=\dfrac{\int\limits_{\Omega\in\mathbb{B}}I^*(x,y)\sigma(\phi(x,y))dxdy}{\int\limits_{\Omega\in\mathbb{B}}\sigma(\phi(x,y))dxdy},~~c_2(\phi)=\dfrac{\int\limits_{\Omega\in\mathcal{B}}I^*(x,y)(1-\sigma(\phi(x,y)))dxdy}{\int\limits_{\Omega\in\mathcal{B}}(1-\sigma(\phi(x,y)))dxdy} c1(ϕ)=Ω∈B∫σ(ϕ(x,y))dxdyΩ∈B∫I∗(x,y)σ(ϕ(x,y))dxdy, c2(ϕ)=Ω∈B∫(1−σ(ϕ(x,y)))dxdyΩ∈B∫I∗(x,y)(1−σ(ϕ(x,y)))dxdy能量函数 F \mathcal{F} F 可以在训练过程中利用梯度反向传播来优化。当时间步 t ≥ 0 t\ge0 t≥0 时,能量函数 F \mathcal{F} F 对 ϕ \phi ϕ 的微分可表示为:
∂ ϕ ∂ t = − ∂ F ∂ ϕ = − ∇ σ ( ϕ ) [ ( I ∗ ( x , y ) − c 1 ) 2 − ( I ∗ ( x , y ) − c 2 ) 2 + γ d i v ( ∇ ϕ ∣ ∇ ϕ ∣ ) ] \dfrac{\partial\phi}{\partial t}=-\dfrac{\partial F}{\partial\phi}=-\nabla\sigma(\phi)[(I^*(x,y)-c_1)^2-(I^*(x,y)-c_2)^2+\gamma div\left(\dfrac{\nabla\phi}{|\nabla\phi|}\right)] ∂t∂ϕ=−∂ϕ∂F=−∇σ(ϕ)[(I∗(x,y)−c1)2−(I∗(x,y)−c2)2+γdiv(∣∇ϕ∣∇ϕ)]其中 ∇ \nabla ∇ 和 d i v div div 分别为空间求导以及散度算子。于是 ϕ \phi ϕ 的更新为:
ϕ i = ϕ i − 1 + Δ t ∂ ϕ i − 1 ∂ t \phi_i=\phi_{i-1}+\Delta t\dfrac{\partial\phi_{i-1}}{\partial t} ϕi=ϕi−1+Δt∂t∂ϕi−1上式可以视为沿着能量函数下降方向的一个隐式的曲线进化,而最优的实例边界 C C C 可以借助迭代拟合 ϕ i − 1 \phi_{i-1} ϕi−1,从而最小化能量函数 F \mathcal{F} F 获得:
inf Ω ∈ B { F ( ϕ ) } ≈ 0 ≈ F ( ϕ i ) \operatorname*{inf}_{\Omega\in\mathcal{B}}\{\mathcal{F}(\phi)\}\approx0\approx\mathcal{F}(\phi_i) Ω∈Binf{F(ϕ)}≈0≈F(ϕi)
输入的数据格式
除输入低水平的图像特征 I u I_u Iu 外,还采用嵌入了图像语言信息的高层深度特征 I f I_f If 来获得更加鲁棒的结果。将 SOLOv2 中所有 FPN 层的 mask 特征 F m a s k F_{\text mask} Fmask 送入到一个卷积层来提取高层特征 I f I_f If。此外,还通过树滤波器来增强 I f I_f If,这利用了最小跨越树(minimal spanning tree?)来建模长距离依赖并保存目标结构。为层级进化构建的整体能量函数为:
F ( ϕ ) = λ 1 ∗ F ( ϕ , I u , c u 1 , c u 2 , B ) + λ 2 ∗ F ( ϕ , I f , c f 1 , c f 2 , B ) , \mathcal F(\phi)=\lambda_1*\mathcal F(\phi,I_u,c_{u_1},c_{u_2},\mathcal B)+\lambda_2*\mathcal F(\phi,I_f,c_{f_1},c_{f_2},\mathcal B),\quad\text{} F(ϕ)=λ1∗F(ϕ,Iu,cu1,cu2,B)+λ2∗F(ϕ,If,cf1,cf2,B),其中 λ 1 \lambda_1 λ1 和 λ 2 \lambda_2 λ2 分别为平衡两种特征的权重, c u 1 c_{u_1} cu1、 c u 2 c_{u_2} cu2、 c f 1 c_{f_1} cf1、 c f 2 c_{f_2} cf2 分别为输入 I u I_u Iu 和 I f I_f If 的均值。
层级初始化
利用 box 投影函数来促进模型自动地生成一个粗糙估计的初始层级 ϕ 0 \phi_0 ϕ0。
通过赋值 GT box 上的每个位置来得到二值化的区域 m b ∈ { 0 , 1 } H × W m^b\in\{0,1\}^{H\times W} mb∈{0,1}H×W。每一个实例预测的 mask 得分 m p ∈ { 0 , 1 } H × W m^p\in\{0,1\}^{H\times W} mp∈{0,1}H×W 被视为前景概率。box 投影函数 F ( ϕ 0 ) b o x \mathcal{F}(\phi_0)_{box} F(ϕ0)box 定义如下:
F ( ϕ 0 ) b o x = P d i c e ( m x p , m x b ) + P d i c e ( m y p , m y b ) \mathcal{F}(\phi_0)_{box}=\mathcal{P}_{dice}(m_x^p,m_x^b)+\mathcal{P}_{dice}(m_y^p,m_y^b) F(ϕ0)box=Pdice(mxp,mxb)+Pdice(myp,myb)其中 m x p m_x^p mxp、 m x b m_x^b mxb、 m y p m_y^p myp、 m y b m_y^b myb 分别为 x x x 和 y y y 坐标轴上mask 预测值 m p m^p mp 和二值化 GT 区域 m b m^b mb 的投影, P d i c e \mathcal{P}_{dice} Pdice 表示这一投影操作具有 1-D dice 系数加权。
4.3 训练和推理
损失函数
损失函数 L L L 包含两部分,分类损失 L c a t e L_{cate} Lcate 和 box 监督下的实例分割损失 L i n s t L_{inst} Linst: L = L c a t e + L i n s t L= L_{cate}+L_{inst} L=Lcate+Linst,其中 L c a t e L_{cate} Lcate 为 Focal 损失, L i n s t L_{inst} Linst 为可微分的层级能量函数:
L i n s t = 1 N p o s ∑ k 1 { p i , j ∗ > 0 } { F ( ϕ ) + α F ( ϕ 0 ) b o x } L_{inst}=\dfrac{1}{N_{pos}}\sum_k\mathbb{1}_{\{p_{i,j}^{*}>0\}}\{\mathcal{F}(\phi)+\alpha\mathcal{F}(\phi_0)_{box}\} Linst=Npos1k∑1{pi,j∗>0}{F(ϕ)+αF(ϕ0)box}其中 N p o s N_{pos} Npos 表示正样本的索引, p i , j ∗ {p_{i,j}^{*}} pi,j∗ 为目标位置 ( i , j ) (i,j) (i,j) 上的类别概率。 1 \mathbb{1} 1 为索引函数,这能确保仅有正的实例 mask 样本才能执行层级进化,如果 p i , j ∗ > 0 p_{i,j}^{*}>0 pi,j∗>0, 1 \mathbb{1} 1 为 1,反之为 0。 α \alpha α 为权重系数,实验设置为 0.3.
推理
推理过程和 SOLOv2 一致:输入图像,利用 NMS 产生有效的 mask。仅有一点不同:采用了额外的一个卷积层来生成高层特征。
五、实验
5.1 数据集
Pascal VOC、COCO、iSAID、LiTS。
5.2 实施细节
AdamW 优化器,8 块 V100(还是够壕~),12 或 36 个 epochs。ResNet + ImageNet 预训练权重作为 Backbone。COCO 数据集:学习率 1 0 − 4 10^{-4} 10−4,batch 16。Pascal VOC 数据集:初始学习率 5 × 1 0 − 5 5\times10^{-5} 5×10−5,batch 8,在这两个数据集上,尺度随机缩放 640-800。iSAID 和 LiTS 有着相同的设置,COCO AP 作为评估指标,非负权重 γ \gamma γ 设为 1 0 − 4 10^{-4} 10−4。
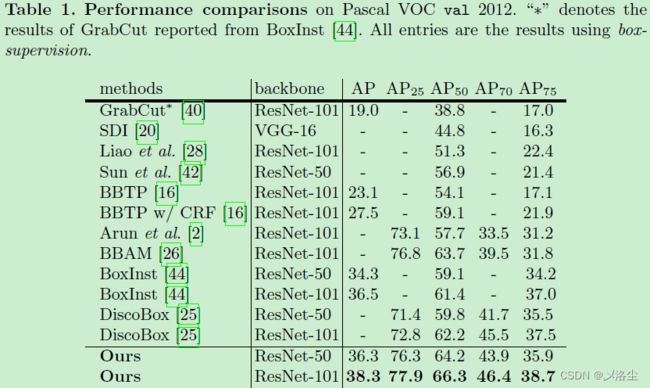
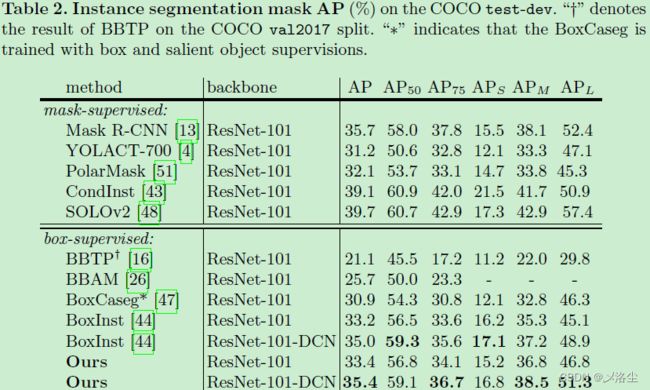
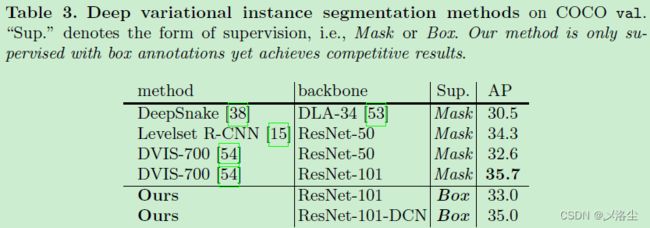
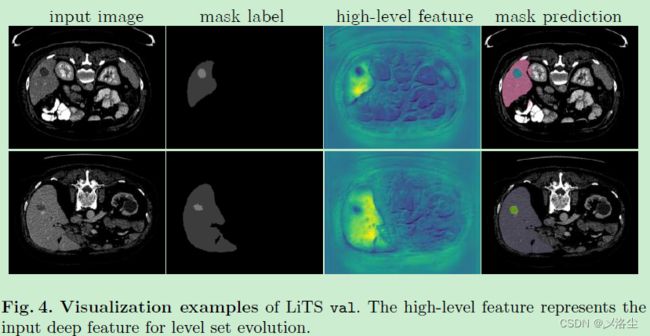
5.3 主要结果
5.4 消融实验
消融实验在 Pascal VOC 数据集上进行:
层级能量
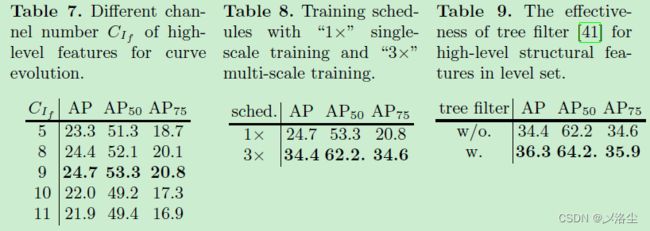
高层特征的通道数量
表 7。
训练计划
表 8。
深度结构特征的有效性
表 9。
六、结论
本文提出了一种 single-shot 的基于 box 的弱监督实例分割方法,能够以端到端的方式迭代地学习一系列层级函数:一种实例感知 mask 图用于预测和作为层级,输入的图像和提取的深度特征用于进化层级曲线,其中一个投影损失函数用于获得初始的边界。通过最小化可微分的能量函数,每个实例的层级能够在相应的 bounding box 标注内迭代地优化,大量的实验表明方法很牛。
写在后面
本文结合若干年前的能量函数方法与现有的深度学习方法进行弱监督实例分割,属实是一锄头挖进往日的纸质期刊堆了,不排除有越来越多的方法~