【论文阅读】Delving into Deep Imbalanced Regression

论文下载
Github
bib:

@INPROCEEDINGS{yang2021delving,
  title		= {Delving into Deep Imbalanced Regression},
  author	= {Yuzhe Yang and Kaiwen Zha and Ying-Cong Chen and Hao Wang and Dina Katabi},
  booktitle	= {ICML},
  year		= {2021},
  pages     = {1--23}
}

1. 摘要

Real-world data often exhibit imbalanced distributions, where certain target values have significantly fewer observations.

Existing techniques for dealing with imbalanced data focus on targets with categorical indices, i.e., different classes.

However, many tasks involve continuous targets, where hard boundaries between classes do not exist.

We define Deep Imbalanced Regression (DIR) as learning from such imbalanced data with continuous targets, dealing with potential missing data for certain target values, and generalizing to the entire target range.

Motivated by the intrinsic difference between categorical and continuous label space, we propose distribution smoothing for both labels and features, which explicitly acknowledges the effects of nearby targets, and calibrates both label and learned feature distributions.

We curate and benchmark large-scale DIR datasets from common real-world tasks in computer vision, natural language processing, and healthcare domains.

Extensive experiments verify the superior performance of our strategies. Our work fills the gap in benchmarks and techniques for practical imbalanced regression problems. Code and data are available at: https://github.com/ YyzHarry/imbalanced-regression.

Notes:

1. 现实数据存在不平衡分布，即某些目标值的观测量明显较少。然而现有的技术集中在分类问题上，在连续目标的预测（回归问题）很少讨论。言简意赅的引出研究问题。
2. 本文的两个贡献：

• LDS: Label Distribution Smoothing. 获得影响回归预测错误率的真实标签分布（连续标签影响）。这一点在分类问题中不存在，分类的标签分布就是影响分类预测的真实分布。
• FDS·：Feature Distribution Smoothing. 平滑标签分布，它的提出是由于一个直觉：相似标签的样本在特征空间也距离近。

2. 前置知识

分类问题中的不平衡问题，一个直观的理解是有些类别样本数量多，而有的类别样本少，甚至没有样本。相比于回归问题中的不平衡问题，分类中的不平衡问题有很多成熟的处理方案， 主要是两种：1. 重采样； 2. 重加权。参考

2.1. 重采样（re-sampling）

简单来说就是不是所有的样本都是等概率的参与运算，降低对应很多样本类别的样本参与运算的概率，提高对应很少样本类别的样本参与运算的概率。这种欠采样方案减少了参与训练的样本。与之相反的还有过采样。

2.2. 重加权（re-weighting）

简单来说就是对不同类别的loss重新加权。

2. 算法描述

从图中可知，连续变量（回归问题）的不平衡主要有两个方面：

• Missing value: 在很大的一个区间中存在未观测的样本。
• Imbalance: 有的区域的观测样本很多，而有的区间观测样本很少（稀疏）。

2.1. Label Distribution Smoothing

$$p(y^{\prime })\triangleq {\int }_{\mathcal{Y}}k(y,y^{\prime })p(y)dy\text{\hspace{1em}(1)}$$
可以理解为标签维度的一个平均，类似于KNN, 只是它是针对全局的。

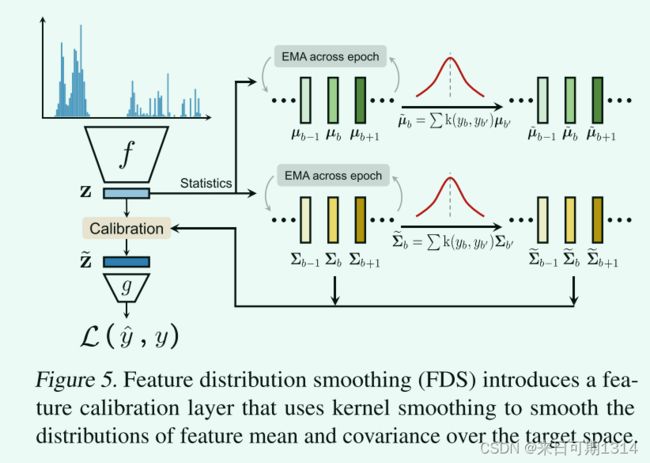
2.2. Feature Distribution Smoothing

$${\mathbf{\mu }}_b=\frac{1}{N_b}\sum _{i=1}^{N_b}{\mathbf{z}}_i\text{\hspace{1em}(2)}$$
$${\mathbf{\Sigma }}_b=\frac{1}{N_b-1}\sum _{i=1}^{N_b}({\mathbf{z}}_i-{\mathbf{\mu }}_b)({\mathbf{z}}_i-{\mathbf{\mu }}_b{)}^{\mathsf{T}}\text{\hspace{1em}(3)}$$

这两个公式表示对于每个类别特征的均值与方差的计算。

$${\mathbf{\mu }}_b=\sum _{b^{\prime }\in \mathcal{B}}k(y_b,y_{b^{\prime }}){\mathbf{\mu }}_b^{\prime }\text{\hspace{1em}(4)}$$
$${\mathbf{\Sigma }}_b=\sum _{b^{\prime }\in \mathcal{B}}k(y_b,y_{b^{\prime }}){\mathbf{\Sigma }}_{b^{\prime }}\text{\hspace{1em}(5)}$$
${\mathbf{\mu }}_b,{\mathbf{\Sigma }}_b$表示平滑后的类别特征均值与方差。

$$\mathbf{z}={\mathbf{\Sigma }}_b^{\frac{1}{2}}{\mathbf{\Sigma }}_b^{-\frac{1}{2}}(\mathbf{z}-{\mathbf{\mu }}_b)+{\mathbf{\mu }}_b$$
这里注意，感觉原有的公式存在歧义，$\mathbf{z}$特征只会与它所属类别的均值与方差进行转化（类似白化操作），在代码里面是这样的。

 for label in torch.unique(labels):
            if label > self.bucket_num - 1 or label < self.bucket_start:
                continue
            elif label == self.bucket_start:
              	pass
            elif label == self.bucket_num - 1:
                pass
            else:
            	# 筛选对应类别的特征进行平滑处理
                features[labels == label] = calibrate_mean_var(
                    features[labels == label],
                    self.running_mean_last_epoch[int(label - self.bucket_start)],
                    self.running_var_last_epoch[int(label - self.bucket_start)],
                    self.smoothed_mean_last_epoch[int(label - self.bucket_start)],
                    self.smoothed_var_last_epoch[int(label - self.bucket_start)])
        return features

3. 总结

这是一篇很容易理解的工作（写得很清晰），而且实验做得很充分。值得注意的是，这篇论文值得我这种不懂高大上理论推导的人学习，从实验观测到处理方法，巧妙的绕过了自己的短板-理论推导，整个文章行文流畅，代码也写得很漂亮，真是太优美了。

文章中提出的两个方法，LDS， FDS其实可以看作是两个独立的trick（技巧），从伪代码中看出没有明显重叠的地方。LDS是re-weighting在回归问题的延伸，FDS有点像BatchNormal。