MVP变换

模型空间/对象空间
——>Model-To-World变换/模型变换（Model）
世界空间
——>World-To-View变换/观察变换（View）
观察空间/照相机空间（以摄像机为原点的坐标系）
——>View-To-Projection变换/投影变换（Projection）
裁剪空间(裁剪图元，为投影做准备)
——>屏幕映射/视口变换
屏幕空间（x,y为对应屏幕上的2d像素坐标）

变换即乘一个矩阵，前三个变换在顶点着色器中相乘最后为一个矩阵，即MVP矩阵。用于将顶点从模型空间转换到裁剪空间，将三维空间中的点，MVP变换后映射到二维平面

模型变换
本质是对三维物体进行缩放、旋转、平移
相对于三维坐标系（即世界坐标系）的原点进行。

缩放矩阵：
沿x轴缩放x倍，沿y轴缩放y倍，沿z轴缩放z倍
[ x, 0, 0, 0
0, y, 0, 0
0, 0, z, 0
0, 0, 0, 1 ]

平移矩阵：
沿x轴平移x个单位，沿y轴平移y个单位，沿z轴平移z个单位
行向量左乘
[1, 0, 0, 0
0, 1, 0, 0
0, 0, 1, 0
x, y, z, 1]
列向量右乘
[1,0,0,x,
0,1,0,y
0,0,1,z
0,0,0,1]

旋转矩阵：
物体绕中心旋转时，通常将中心移到原点，进行操作，在移回。
M = Mt^-1 · Mr · Mt

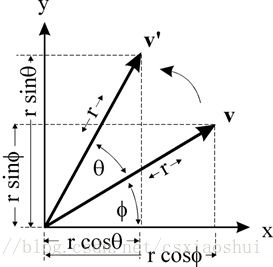
二维旋转
三角函数展开cos (α ± β) = cosα cosβ ∓ sinβ sinα

绕x轴旋转
[1, 0, 0, 0
0, cosθ, -sinθ, 0
0, sinθ, cosθ, 0
0, 0, 0, 1]
绕y轴旋转
[cosθ, 0, sinθ, 0
0, 1, 0, 0
-sinθ, 0, cosθ, 0
0, 0, 0, 1]
绕z轴旋转
[cosθ, -sinθ, 0, 0
sinθ, cosθ, 0, 0
0, 0, 1, 0
0, 0, 0, 1]
注：平移缩放旋转矩阵相乘的顺序不同，最终矩阵不同（矩阵不遵守交换律）一般缩放——旋转——平移
即M = Mtr · Mt^-1 · Mr · Mt · Ms

视觉变换
摄像机的变换是在世界空间中先旋转后平移获得，需先反方向平移变换，在反向旋转变换。若观察空间坐标系与世界空间坐标系相反（如unity），最后需对z轴反向
V =
[1, 0, 0, 0
0, 1, 0, 0
0, 0, -1, 0
0, 0, 0, 0] · Mr · Mt
在物体与摄像机相对位置不变的情况下让摄像机位于（0，0，0），将变换摄像机的矩阵作用于物体上就可得到观察空间中的坐标
摄像机：位置p，观察方向g，上方t
标准位置：原点（0，0，0），up指向y轴，Look-at指向z轴

投影变换
为裁剪做准备
将3D图形投影到2D平面上

正交投影：
假设摄像机在无限远，投影物体不存在近大远小，都是以平行光投影到进平面。即把摄像机固定在原点。look-at为-z轴，up为y轴。
丢弃z坐标，或另z坐标为0，最后缩放到一个[-1，1]的区间


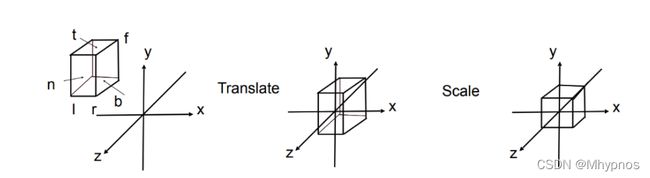
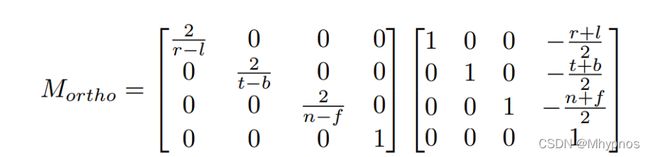
先平移至原点，再缩放

透视投影：
遵循近大远小。保持近平面不变，远平面压缩为近平面（z值不变）
透视投影先将远平面f挤压成近平面n的大小，在进行正射投影
n为近点，f为远点

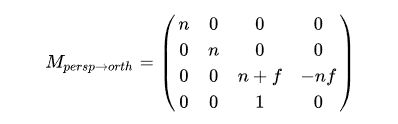
MVP变换
MVP变换

视口变换
屏幕映射：将投影变换获得的标准二维平面调整到显示屏幕，本质为缩放平移的过程
[-1,1]转换成[0，width]和[0，height],z方向不变