常用神经网络_2_ 残差网络 —> ResNet —> DenseNet
残差网络&ResNet&DenseNet
- 1、前言
-
- 1.1、残差块
- 2、残差网络:ResNet
-
- 2.1、ResNet的网络结构
- 3、残差网络:DenseNet
-
- 3.2、设计理念
- 3.3、网络结构
1、前言
在VGG中,卷积网络达到了19层,在GoogLeNet中,网络史无前例的达到了22层。那么,网络的精度会随着网络的层数增多而增多吗?在深度学习中,网络层数增多一般会伴着下面几个问题
计算资源的消耗
模型容易过拟合
梯度消失/梯度爆炸问题的产生
问题1可以通过GPU集群来解决,对于一个企业资源并不是很大的问题;问题2的过拟合通过采集海量数据,并配合Dropout正则化等方法也可以有效避免;问题3通过Batch Normalization也可以避免。貌似我们只要无脑的增加网络的层数,我们就能从此获益,但实验数据给了我们当头一棒。
作者发现,随着网络层数的增加,网络发生了退化(degradation)的现象:随着网络层数的增多,训练集loss逐渐下降,然后趋于饱和,当你再增加网络深度的话,训练集loss反而会增大。注意这并不是过拟合,因为在过拟合中训练loss是一直减小的。
当网络退化时,浅层网络能够达到比深层网络更好的训练效果,这时如果我们把低层的特征传到高层,那么效果应该至少不比浅层的网络效果差,或者说如果一个VGG-100网络在第98层使用的是和VGG-16第14层一模一样的特征,那么VGG-100的效果应该会和VGG-16的效果相同。所以,我们可以在VGG-100的98层和14层之间添加一条直接映射(Identity Mapping)来达到此效果。
从信息论的角度讲,由于DPI(数据处理不等式)的存在,在前向传输的过程中,随着层数的加深,Feature Map包含的图像信息会逐层减少,而ResNet的直接映射的加入,保证了 L+1层的网络一定比 L层包含更多的图像信息。
基于这种使用直接映射来连接网络不同层直接的思想,残差网络应运而生。
1.1、残差块
残差网络是由一系列残差块组成的,残差块分成两部分直接映射部分和残差部分。

图1中的Weight在卷积网络中是指卷积操作,addition是指单位加操作。
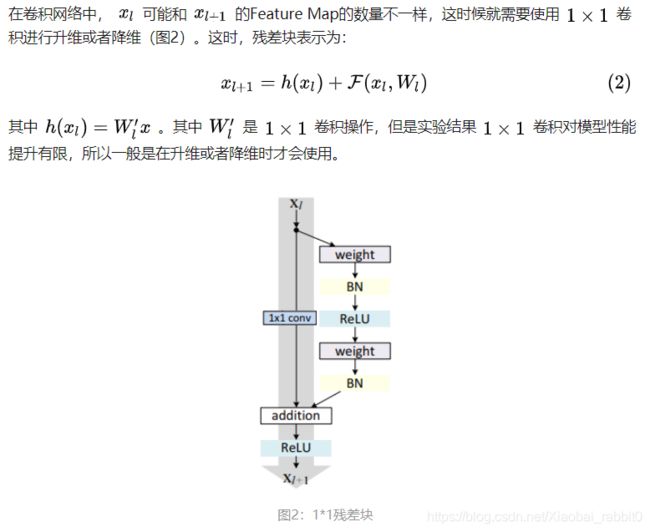
一般,这种版本的残差块叫做resnet_v1,keras代码实现如下:
def res_block_v1(x, input_filter, output_filter):
res_x = Conv2D(kernel_size=(3,3), filters=output_filter, strides=1, padding='same')(x)
res_x = BatchNormalization()(res_x)
res_x = Activation('relu')(res_x)
res_x = Conv2D(kernel_size=(3,3), filters=output_filter, strides=1, padding='same')(res_x)
res_x = BatchNormalization()(res_x)
if input_filter == output_filter:
identity = x
else: #需要升维或者降维
identity = Conv2D(kernel_size=(1,1), filters=output_filter, strides=1, padding='same')(x)
x = keras.layers.add([identity, res_x])
output = Activation('relu')(x)
return output
2、残差网络:ResNet
14年的VGG才19层,而15年的ResNet多达152层,这在网络深度完全不是一个量级上,所以如果是第一眼看这个图的话,肯定会觉得ResNet是靠深度取胜。事实当然是这样,但是ResNet还有架构上的trick,这才使得网络的深度发挥出作用,这个trick就是残差学习(Residual learning)。
2.1、ResNet的网络结构
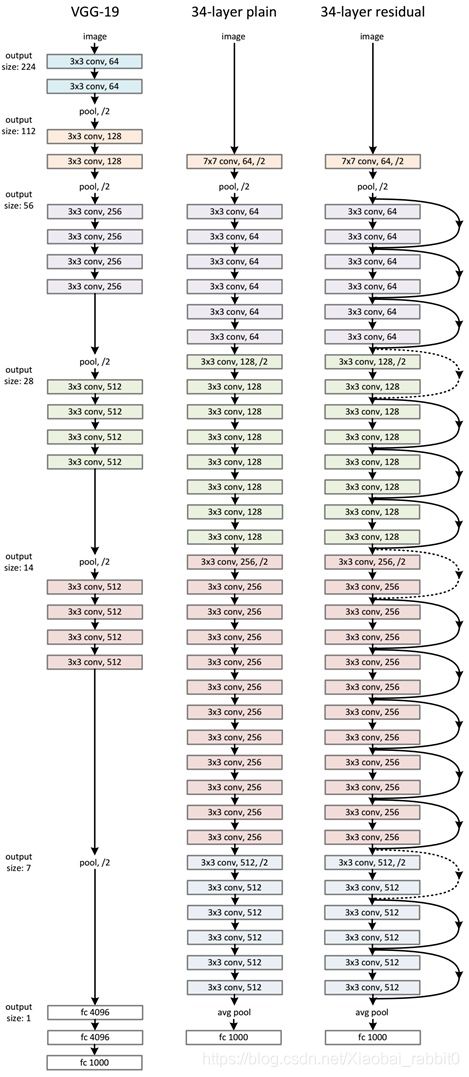
ResNet网络是参考了VGG19网络,在其基础上进行了修改,并通过短路机制加入了残差单元,如图所示。变化主要体现在ResNet直接使用stride=2的卷积做下采样,并且用global average pool层替换了全连接层。ResNet的一个重要设计原则是:当feature map大小降低一半时,feature map的数量增加一倍,这保持了网络层的复杂度。从图5中可以看到,ResNet相比普通网络每两层间增加了短路机制,这就形成了残差学习,其中虚线表示feature map数量发生了改变。图5展示的34-layer的ResNet,还可以构建更深的网络如表所示。从表中可以看到,对于18-layer和34-layer的ResNet,其进行的两层间的残差学习,当网络更深时,其进行的是三层间的残差学习,三层卷积核分别是1x1,3x3和1x1,一个值得注意的是隐含层的feature map数量是比较小的,并且是输出feature map数量的1/4。

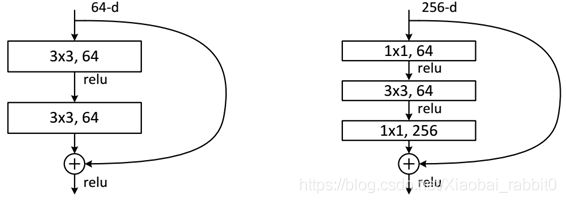
下面我们再分析一下残差单元,ResNet使用两种残差单元,如图6所示。左图对应的是浅层网络,而右图对应的是深层网络。对于短路连接,当输入和输出维度一致时,可以直接将输入加到输出上。但是当维度不一致时(对应的是维度增加一倍),这就不能直接相加。有两种策略:(1)采用zero-padding增加维度,此时一般要先做一个downsamp,可以采用strde=2的pooling,这样不会增加参数;(2)采用新的映射(projection shortcut),一般采用1x1的卷积,这样会增加参数,也会增加计算量。短路连接除了直接使用恒等映射,当然都可以采用projection shortcut。
作者对比18-layer和34-layer的网络效果,如图7所示。可以看到普通的网络出现退化现象,但是ResNet很好的解决了退化问题。
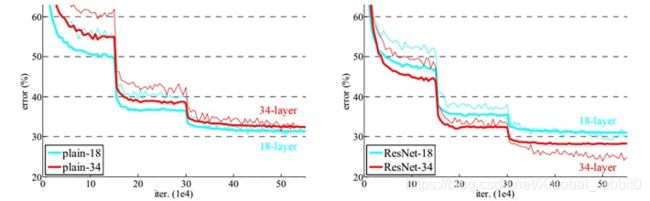
最后展示一下ResNet网络与其他网络在ImageNet上的对比结果,如表2所示。可以看到ResNet-152其误差降到了4.49%,当采用集成模型后,误差可以降到3.57%。

3、残差网络:DenseNet
DenseNet:比ResNet更优的CNN模型
在计算机视觉领域,卷积神经网络(CNN)已经成为最主流的方法,比如最近的GoogLenet,VGG-19,Incepetion等模型。CNN史上的一个里程碑事件是ResNet模型的出现,ResNet可以训练出更深的CNN模型,从而实现更高的准确度。ResNet模型的核心是通过建立前面层与后面层之间的“短路连接”(shortcuts,skip connection),这有助于训练过程中梯度的反向传播,从而能训练出更深的CNN网络。今天我们要介绍的是DenseNet模型,它的基本思路与ResNet一致,但是它建立的是前面所有层与后面层的密集连接(dense connection),它的名称也是由此而来。DenseNet的另一大特色是通过特征在channel上的连接来实现特征重用(feature reuse)。这些特点让DenseNet在参数和计算成本更少的情形下实现比ResNet更优的性能,DenseNet也因此斩获CVPR 2017的最佳论文奖。

3.2、设计理念
相比ResNet,DenseNet提出了一个更激进的密集连接机制:即互相连接所有的层,具体来说就是每个层都会接受其前面所有层作为其额外的输入。图1为ResNet网络的连接机制,作为对比,图2为DenseNet的密集连接机制。可以看到,ResNet是每个层与前面的某层(一般是2~3层)短路连接在一起,连接方式是通过元素级相加。而在DenseNet中,每个层都会与前面所有层在channel维度上连接(concat)在一起(这里各个层的特征图大小是相同的,后面会有说明),并作为下一层的输入。对于一个 L层的网络,DenseNet共包含 L(L+1)/2个连接,相比ResNet,这是一种密集连接。而且DenseNet是直接concat来自不同层的特征图,这可以实现特征重用,提升效率,这一特点是DenseNet与ResNet最主要的区别。
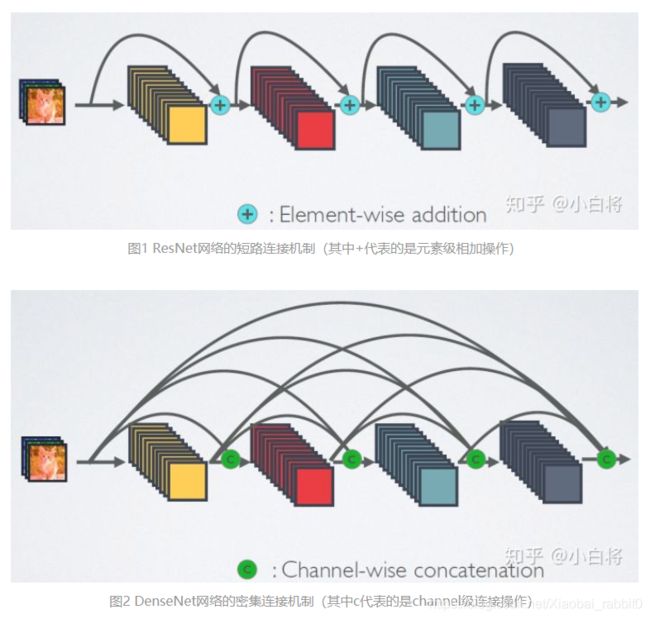
DenseNet的前向过程如图3所示,可以更直观地理解其密集连接方式,比如 h3 的输入不仅包括来自 h2 的 x2 ,还包括前面两层的 x1 和 x2 ,它们是在channel维度上连接在一起的。

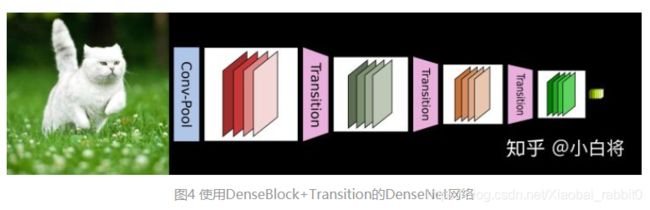
CNN网络一般要经过Pooling或者stride>1的Conv来降低特征图的大小,而DenseNet的密集连接方式需要特征图大小保持一致。为了解决这个问题,DenseNet网络中使用DenseBlock+Transition的结构,其中DenseBlock是包含很多层的模块,每个层的特征图大小相同,层与层之间采用密集连接方式。而Transition模块是连接两个相邻的DenseBlock,并且通过Pooling使特征图大小降低。图4给出了DenseNet的网路结构,它共包含4个DenseBlock,各个DenseBlock之间通过Transition连接在一起。
3.3、网络结构
如前所示,DenseNet的网络结构主要由DenseBlock和Transition组成,如图5所示。下面具体介绍网络的具体实现细节。

在DenseBlock中,各个层的特征图大小一致,可以在channel维度上连接。DenseBlock中的非线性组合函数 H() 采用的是BN+ReLU+3x3 Conv的结构,如图6所示。另外值得注意的一点是,与ResNet不同,所有DenseBlock中各个层卷积之后均输出 K 个特征图,即得到的特征图的channel数为 K ,或者说采用 K 个卷积核。 K 在DenseNet称为growth rate,这是一个超参数。一般情况下使用较小的 K (比如12),就可以得到较佳的性能。假定输入层的特征图的channel数为 K0,那么 L 层输入的channel数为 K0+K(L-1) ,因此随着层数增加,尽管 K 设定得较小,DenseBlock的输入会非常多,不过这是由于特征重用所造成的,每个层仅有 K 个特征是自己独有的。