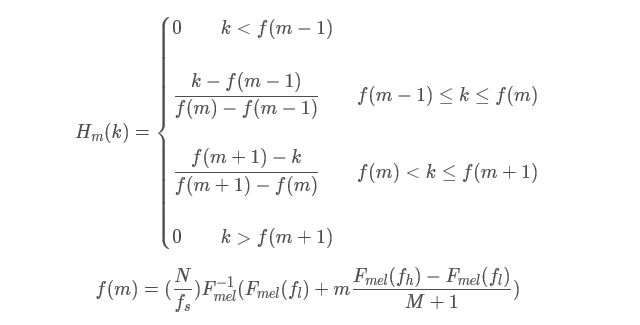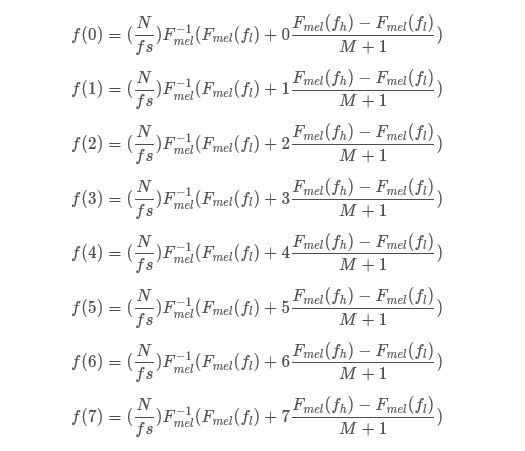音频(六)Mel滤波器组_原理简介
为什么会产生出Mel 这种尺度的机制呢?
人耳朵具有特殊的功能,可以使得人耳朵在嘈杂的环境中,以及各种变异情况下仍能正常的分辨出各种语音;
其中,耳蜗有关键作用;
耳蜗实质上的作用相当于一个滤波器组,耳蜗的滤波作用是在对数频率尺度上进行的,在1000HZ以下为线性尺度,1K HZ以上为对数尺度,使得人耳对低频信号敏感,高频信号不敏感;
也就是说,当初产生这种机制主要是为了模拟,人耳朵的听觉机制;
根据这一原则,从而研制出来了Mel频率滤波器组,
所以,Mel滤波器组的在靠近低频出越密集,越靠近高频出,滤波器越稀疏;
1. 简介 梅尔刻度
- 为什么需要 Mel 刻度:
MEL刻度模拟人耳对不同频率语音的感知:
研究表明,人类对频率的感知并不是线性的,并且对低频信号的感知要比高频信号敏感。对1kHz以下,与频率成线性关系,对1kHz以上,与频率成对数关系。频率越高,感知能力就越差。
例如,人们可以比较容易地发现500和1000Hz的区别,但很难发现7500和8000Hz的区别。
- Mel (melody)刻度定义:
这时,梅尔标度(the Mel Scale)被提出,它是Hz的非线性变换,对于以mel scale为单位的信号,可以做到人们对于相同频率差别的信号的感知能力几乎相同。
M e l ( f ) = 2595 ∗ l o g 10 ( 1 + f 700 ) , Mel(f) = 2595* log_{10}(1+ \frac{f}{700} ), Mel(f)=2595∗log10(1+700f),
f = 700 ( 1 0 m 2595 − 1 ) . f=700(10^\frac{m}{2595} −1). f=700(102595m−1).
M 被称作 Mel 频率;
![]()
观察上图:
从Hz到mel的映射图,由于它们是log的关系,
当频率较小时,mel随Hz变化较快;
当频率很大时,mel的上升很缓慢,曲线的斜率很小。
这说明了人耳对低频音调的感知较灵敏,在高频时人耳是很迟钝的,梅尔标度滤波器组启发于此, 从而 梅尔滤波器 的 分布情况 受启发于此。
![]()
如上图所示,40个三角滤波器组成滤波器组,低频处滤波器密集,门限值大,高频处滤波器稀疏,门限值低。恰好对应了频率越高人耳越迟钝这一客观规律。上图所示的滤波器形式叫做等面积梅尔滤波器(Mel-filter bank with same bank area),在人声领域(语音识别,说话人辨认)等领域应用广泛,但是如果用到非人声领域,就会丢掉很多高频信息。
![]()
如上图所示,如果用到非人声领域,这时常用的是等高梅尔滤波器(Mel-filter bank with same bank height):
2. Mel频率与普通频率
2.1 Mel 与f 两者的转换关系
梅尔频率与实际频率的关系如下:
F m e l ( f ) = 2595 ∗ l o g 10 ( 1 + f 700 ) , F_{mel}(f) = 2595* log_{10}(1+ \frac{f}{700} ), Fmel(f)=2595∗log10(1+700f),
f = 700 ( 1 0 m 2595 − 1 ) . f=700(10^\frac{m}{2595} −1). f=700(102595m−1).
F m e l ( f ) F_{mel}(f) Fmel(f) j简写成m, 是以Mel为单位的感知频率, f f f是以Hz为单位的实际频率;
注意, 如果对数以e为底, 则系数的取值为1125
Mel滤波器组就是一系列的三角形滤波器,通常有40个或80个,在中心频率点响应值为1,在两边的滤波器中心点衰减到0,如下图:
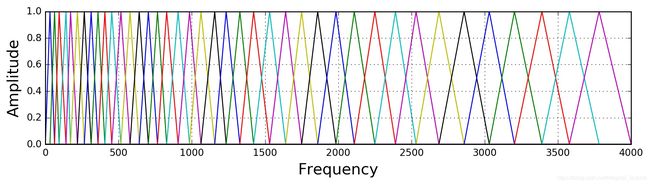
具体公式可以写为:
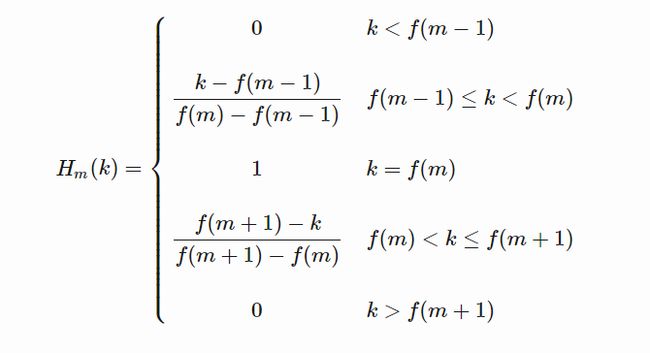
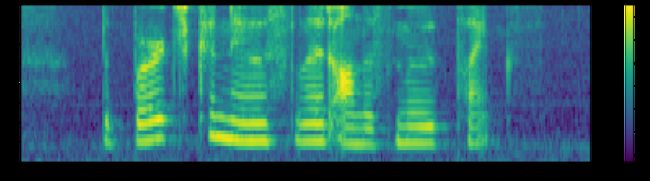
2.2 生成Mel 语谱图
注意,log mel-filter bank outputs和“FBANK features说的是同一个东西,
他们本质上都指的是经过 Mel filter, Mel 滤波器的输出 ;
最后在能量谱上应用Mel滤波器组,其公式为:
Y t ( m ) = ∑ k = 1 N H m ( k ) ∣ X t ( k ) ∣ 2 Y_t(m) = \sum^{N}_{k=1} H_{m}(k)|X_{t}(k)|^2 Yt(m)=k=1∑NHm(k)∣Xt(k)∣2
其中,k表示FFT变换后的编号,m表示mel滤波器的编号。
low_freq_mel = 0
high_freq_mel = 2595 * np.log10(1 + (sample_rate / 2) / 700)
print(low_freq_mel, high_freq_mel)
0 2146.06452750619
nfilt = 40
mel_points = np.linspace(low_freq_mel, high_freq_mel, nfilt + 2) # 所有的mel中心点,为了方便后面计算mel滤波器组,左右两边各补一个中心点
hz_points = 700 * (10 ** (mel_points / 2595) - 1)
fbank = np.zeros((nfilt, int(NFFT / 2 + 1))) # 各个mel滤波器在能量谱对应点的取值
bin = (hz_points / (sample_rate / 2)) * (NFFT / 2) # 各个mel滤波器中心点对应FFT的区域编码,找到有值的位置
for i in range(1, nfilt + 1):
left = int(bin[i-1])
center = int(bin[i])
right = int(bin[i+1])
for j in range(left, center):
fbank[i-1, j+1] = (j + 1 - bin[i-1]) / (bin[i] - bin[i-1])
for j in range(center, right):
fbank[i-1, j+1] = (bin[i+1] - (j + 1)) / (bin[i+1] - bin[i])
print(fbank)
[[0. 0.46952675 0.93905351 … 0. 0. 0. ]
[0. 0. 0. … 0. 0. 0. ]
[0. 0. 0. … 0. 0. 0. ]
…
[0. 0. 0. … 0. 0. 0. ]
[0. 0. 0. … 0. 0. 0. ]
[0. 0. 0. … 0.14650797 0.07325398 0. ]]
filter_banks = np.dot(pow_frames, fbank.T)
filter_banks = np.where(filter_banks == 0, np.finfo(float).eps, filter_banks)
filter_banks = 20 * np.log10(filter_banks) # dB
print(filter_banks.shape)
(349, 40)
plot_spectrogram(filter_banks.T, 'Filter Banks')
3. Mel滤波器组设计的总体思想
3.1 中心频率的选取
在语音的频谱范围内设置若干带通滤波器 H m ( k ) H_m(k) Hm(k), 1 ≤ m ≤ M 1≤m≤M 1≤m≤M,M为滤波器的个数(M一般取24)。
每个滤波器具有三角滤波特性,其中心频率为 f ( m ) f(m) f(m), 1 ≤ m ≤ M 1≤m≤M 1≤m≤M。
f l f_{l} fl为滤波器频率范围内的最低频率,
f h f_{h} fh为滤波器频率范围内的最高频率,
N为DFT(或FFT)时的长度,
f s f_{s} fs为采样频率,
F m e l F_{mel} Fmel的逆函数:
F m e l − 1 ( m ) = 700 ( 1 0 m 2595 − 1 ) . F^{-1}_{mel}(m) =700(10^\frac{m}{2595} −1). Fmel−1(m)=700(102595m−1).
3.2 分析与设计
以M=6(6个滤波器)为例, f l f_{l} fl, f h f_{h} fh, f s f_{s} fs、 N N N、 M M M的值一旦确定就固定不变。
将Mel 频率尺度上的 F m e l ( f l ) F_{mel}(f_l) Fmel(fl)至 F m e l ( f h ) F_{mel}(f_h) Fmel(fh)
的Mel频率范围均分为M+1=7段,
产生M+2=8个Mel频率值。
F m e l − 1 ( F m e l ( f l ) + i F m e l ( f h ) − F m e l ( f l ) M + 1 ) F^{-1}_{mel}(F_{mel}(f_l)+i\cfrac{F_{mel}(f_h)-F_{mel}(f_l)}{M+1}) Fmel−1(Fmel(fl)+iM+1Fmel(fh)−Fmel(fl))
0 ≤ i ≤ 8 0≤i≤8 0≤i≤8
分别求出这M+2=8个实际频率值对应的FFT点数
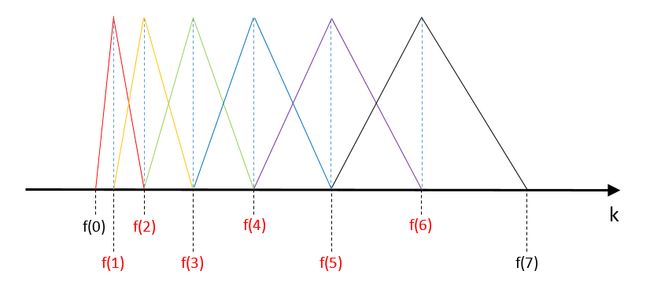
f(1)、f(2)、f(3)、f(4)、f(5)、f(6)分别为第1,2,3,4,5,6个滤波器的中心频率对应的FFT点数(向上取整),设计M=6个滤波器。
- m = 1(第1个滤波器)
当 f(m-1) 当 f(m) 当 f(m-1) 当 f(m-1) 当 f(m-1) 当 f(m-1) 当 f(m-1) 原始的Mel 滤波器,实现过程如下: 主要有分为三步: 映射到Mel 尺度上的原因,该Mel尺度的频率是拟合了人耳的线性变换, 将上述步骤一中, (K + 2) 个Mel 频率点 映射到(K + 2) 普通频率HZ上 h ( i ) h(i) h(i) 将步骤二中, (K + 2) 个普通频率取整到最接近的 frequency bin 频率上 f ( i ) f(i) f(i); 此时得到的 f ( i ) f(i) f(i) 即是各个滤波器的中心频率, 生成三角滤波器; 采用python中 因此详细研究了一下python中 这里我们主要关注数学表达,数学表达搞清后写代码自然不是难事。 通常情况下, m = 2595 l g ( 1 + f / 700 ) , m=2595lg(1+ f/700), m=2595lg(1+f/700), f = 700 ( 1 0 2595 m − 1 ) . f=700(10^{\frac{2595}{m}} −1). f=700(10m2595−1). 求出 Mel 滤波器中,对应的等间隔的Mel频率: 假如有10个Mel滤波器 首先要选择一个最高频率和最低频率,通常最高频率为8000Hz,最低频率为300Hz。 使用从频率转换为Mel频率的公式将 由于有10个滤波器,每个滤波器针对两个频率的样点,样点之间会进行重叠处理,因此需要12个点,意味着需要在401.25和2834.99之间再线性间隔出10个附加点,如: m(i)=401.25,622.50,843.75,1065.00,1286.25,1507.50,1728.74,1949.99,2171.24,2392.49,2613.74,2834.99 现在使用从Mel频率转换为频率的公式将它们转换回赫兹: h(i)=300,517.33,781.90,1103.97,1496.04,1973.32,2554.33,3261.62,4122.63,5170.76,6446.70,8000 将频率映射到最接近的DFT频率 此时得到的 f(i), 便是 Mel 滤波器组中 各个滤波器的中心频率; 在得到各个滤波器的中心频率后, 便可知 各个滤波器对应的频率响应; 将功率谱形成的语谱图通过 Mel 滤波器组,便得到 Mel Spectrogram; 如下图,函数输入为(frequencies,htk)frequencies为待转化的频率,htk为是否用HTK formula进行转化,默认htk=False。 官方文档是这么解释的:htk,bool, If True, use HTK formula to convert Hz to mel. Otherwise (False), use Slaney’s Auditory Toolbox. 那么这里的Slaney’s Auditory Toolbox是怎么计算mel频率的呢? 对于小于1000Hz的频率,进行线性转化, m = 3 f 200 m=\frac{3f}{200} m=2003f 对于大于(等于)1000Hz的频率,对数转化, m = 15 + l n f 1000 l n 6.4 27 m=15+\frac{ln\frac{f}{1000}}{\frac{ln6.4}{27}} m=15+27ln6.4ln1000f, 其中, 15是因为15 = 3 ∗ 1000 200 \frac{3*1000}{200} 2003∗1000, 至于6.4和27怎么来的我也不太清楚……
4. Mel 滤波器生成的具体步骤
librosa库,发现从Hz频率到Mel频率有两种转换方式,而默认的方式并不是按照我们熟知的公式进行转换的,librosa库中与mel频谱有关的源代码。hz频率f ff与mel频谱m mm通过如下公式转换4.1 Mel 滤波器中等间隔的Mel 频率:
(在实际应用中通常一组Mel滤波器组有26个滤波器。)300Hz转换为401.25Mels,8000Hz转换为2834.99Mels,
4.2 Mel 频率转换为 HZ:
def hz2mel(hz):
'''把频率hz转化为梅尔频率'''
return 2595 * numpy.log10(1 + hz / 700.0)
def mel2hz(mel):
'''把梅尔频率转化为hz'''
return 700 * (10 ** (mel / 2595.0) - 1)
4.3 Mel 滤波器中心频率
其中 257 = N , N取值为 DFT 长度中的有效保留值,
![]()
![]()
![]()
![]()
5. librosa 库的实现原理是:
根据代码来看是这样:
// An highlighted block
def hz_to_mel(frequencies, htk=False):
"""Convert Hz to Mels
Examples
--------
>>> librosa.hz_to_mel(60)
0.9
>>> librosa.hz_to_mel([110, 220, 440])
array([ 1.65, 3.3 , 6.6 ])
Parameters
----------
frequencies : number or np.ndarray [shape=(n,)] , float
scalar or array of frequencies
htk : bool
use HTK formula instead of Slaney
Returns
-------
mels : number or np.ndarray [shape=(n,)]
input frequencies in Mels
See Also
--------
mel_to_hz
"""
frequencies = np.asanyarray(frequencies)
if htk:
return 2595.0 * np.log10(1.0 + frequencies / 700.0)
# Fill in the linear part
f_min = 0.0
f_sp = 200.0 / 3
mels = (frequencies - f_min) / f_sp
# Fill in the log-scale part
min_log_hz = 1000.0 # beginning of log region (Hz)
min_log_mel = (min_log_hz - f_min) / f_sp # same (Mels)
logstep = np.log(6.4) / 27.0 # step size for log region
if frequencies.ndim:
# If we have array data, vectorize
log_t = frequencies >= min_log_hz
mels[log_t] = min_log_mel + np.log(frequencies[log_t] / min_log_hz) / logstep
elif frequencies >= min_log_hz:
# If we have scalar data, heck directly
mels = min_log_mel + np.log(frequencies / min_log_hz) / logstep
return mels