空间复杂性1：（SPACE,NSPACE,PSPACE,L,NL,CONL）
目录
一：空间复杂性
二：空间复杂性类
证明：SAT SPACE(O(n))
证明：NFA是否接受所有字符串的补问题 属于 NSPACE(O(n))
三：萨维奇定理
四：PSPACE类
证明：带量词的布尔公式 属于 PSPACE.
五：P,NP与PSPACE关系
六：L和NL
对数空间复杂类
对数空间TM的格局
八：NL=coNL
总结图：(集合关系图)
一：空间复杂性
1：设M是一个处处停机(在所有输入都停机)的确定性图灵机(DTM),则M的空间复杂度为：
函数f:N
N,其中f(n)是M在任何长度为n的输入上最多扫描f(n)个不同的带方格。
也称：M在空间f(n)内运行。
即：DTM M在长度为n的输入上最多用了(读或写)f(n)个格子。
2：设NTM M在所有输入的所有计算分支上都停机。(非确定性图灵判定机)，则M的空间复杂度为：M在任何长度为n的输入上，在任何计算分支上所扫描带方格的最大数f(n)。
即：NTM的计算路径是树，选择最长路径所扫描最多带格子数作为时间复杂度。
二：空间复杂性类
1：
2:
证明：SAT 
SPACE(O(n))
1:
可满足的意思是：x与y的赋值会使布尔公式的值为真（1）。如：x=1,y=0;
DTM
="对输入的<
>，
1：对
的每种赋值：
2：计算
3：若
分析：因为每一次循环可以重用带子的同一部分，即：每次完成一次判断后，擦去原赋值重新写新赋值。机器存储当前m个变量的赋值可以用O(m)空间，变量m1的输入长度最多为n,m
n,所以总空间为O(f(n)).核心：空间可以重复利用
证明：NFA是否接受所有字符串的补问题 属于 NSPACE(O(n))
,
的意思是字母表所有符号的闭包，相当于接受所有语言的意思。
它的补问题：
至少有一个串不会被NFA接受
pf:
思想：猜NFA拒绝的串，用非确定型线性空间跟踪NFA状态。
NTM N="对输入的,M是NFA:
1:在NFA初始状态放一个标记；
2:反复执行
次下列语句（q是M的状态数);
3:非确定性的选择一个输入符号，来改变M状态上标记的位置，来模拟读取这个符号；
（意思是：每读一个新符号就进入一个新状态。）
4：若在执行2,3的过程中，某一时刻所有标记都不落在接受状态上，则接受；否则拒绝。“
分析：如果N接受一个字符串，它一定接受长度小于的字符串，因为任何更长的字符串一定会有重复出现标记位置。所有标记位置最多种，故而：只需要O(q)空间存储标记，
.得出结论：在O(n)空间内运行。
三：萨维奇定理
用确定性型空间来模拟非确定型空间，只有平方的增长。也就是：任何消耗f(n)空间的NTM可以转换为消耗
的DTM.
这一定理也说明了：
但是时间就没用这样的性质，因为空间是可以重复利用的。
，因为DTM遍历每一个计算分支是指数增长的。
即：
四：PSPACE类
PSPACE是在DTM上用多项式空间内可判定的语言类。
可以理解：PSPACE是SPACE中的多项式空间，NPSPACE是NSPACE中的多项式空间，而SPACE=NSPACE,故而：PSPACE=NPSPACE.
证明：带量词的布尔公式 属于 PSPACE.
带量词布尔公式：（布尔公式中含有任意与存在）
对于x的某个值，的值为真；
:对于x的每个值，的值为真。
全带量词的布尔公式：没有自由变元的带量词布尔公式（每个变量只能取0或1）
DTM T="对于输入的<
1:若
2:若
,则输出
;
3:若
,则输出
."
分析：设变量个数为m个，则递归深度最多等于变量个数,故消耗总空间为O(m).
五：P,NP与PSPACE关系
关系显然成立,在t(n)
n(读完输入)条件下，任何在时间t(n)内运行的图灵机最多能消耗t(n)空间。也就是说：图灵机每运行一次（运行步数为一）其访问的单元格子数不会超过一。
目前能确定：P与EXP真包含，也就是说指数类包含多项式类，但是P与NP，NP与SPACE是否能取等，目前还无法得知。
六：L和NL
下面考虑比P还小的空间：亚线性空间--L(对数空间类)和NL(非确定性对数空间类)
亚线性函数f(n):
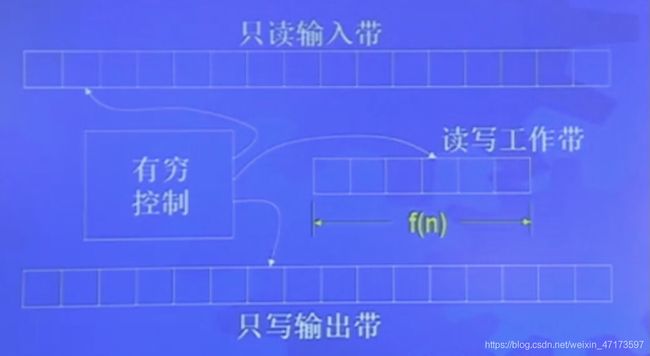
亚线性空间TM(原理：把输入和工作区分来，输入作为只读，读写工作在工作带上进行，这条工作带是：亚线性空间的)
具体：一条输入带（外存）作为只读（不是单向，来回读），不计入时间复杂性；一条工作带（内存）可读写，计入时间复杂度。
（将输入输出与真正工作的进行分离，更本质的考察时间复杂性）
对数空间复杂类
考虑log原因：具有稳健性，语言性质与机器模型和编码方法无关；足以表示指向输入的指针对数空间足以解决有趣的数学问题。
语言：L={
}属于L.
方法：工作带用二进制形式分别数读入带的0和1的个数。唯一需要的空间只是这两个计数器。显然是：非线性的。
证明：PATHNL.
1:如果采取确定型验证机，先写下起点,确定是否为s.然后我们在工作带只计入当前两个顶点 ，然后查输入带上两点之间是否有边。最后确定终点是不是t即可。
2：采取NTM
NTM M="输入的:
1:令当前顶点为s;
2:执行下列步骤m步：（顶点数为m）
3：若当前顶点为t，则接受；
4：非确定选择下一个顶点，检查当前顶点与此顶点是否有边；
5：有边，令当前顶点等于下一顶点；否则，拒绝
6：执行m步后还不接受，拒绝。"
分析：工作带只保存了当前顶点，需要
空间
对数空间TM的格局
若M是有一条只读输入带的TM，则M在输入串w的格局：由状态，工作带内容，两个带头的位置所组成。（输入作为只读不构成格局的一部分）
若：亚线性f(n)空间TM有c个状态，g个输入带符号，则TM的格局总数：
（n输入长度，f(n)带格子数）
带头位置：n个中1个，工作带头f(n)1个
每个格局长度：logn(输入带头位置)+O(f(n)) (指针位置)得出：
八：NL=coNL
非确定对数空间类，只要：运行带格子数大于logn ,则：语言关于补封闭。
确定性复杂类对补封闭。（L,P,PSPACE,EXP）
因为只有一个路径，要么接受要么拒绝。主要有能接受这种语言的图灵机，只要将状态取反，那么就对应着接受补语言的图灵机。
非确定复杂类的补语言确定难度：
只要有一个计算分支接受就接受该语言，也就是分支中有接受有拒绝，取反后，依然有接受有拒绝，故而没意义。
时间类：NP与coNP关系未知。
空间类：NSPACE(f(n))=coNSPACE(f(n)),要求：f(n)
log n.
即：NL=coNL.
应用：
总结图
