深度学习笔记 4 过拟合+欠拟合+解决方案

目录

1. 偏差与方差

2. 产生原因

3.解决欠拟合(高偏差)的方法

3.1 模型复杂化

3.2 增加更多的特征

3.3 调整参数和超参数

3.4 增加训练数据(效果不明显）

3.5 降低正则化约束

4. 解决过拟合(高方差)的方法

 4.1 增加训练数据数

4.2 使用正则化约束

4.3 批归一化 BN

4.4 使用Dropout

4.5 提前结束训练

4.6 减少特征数

4.7 调整参数和超参数

4.8 降低模型的复杂度

5.正则化 

 5.1 L1、L2正则化(Regularization)

 5.2 正则化为什么能够防止过拟合

 6 Droupout丢弃法

7 数据增强

7.1 线性变换

7.2 标签平滑

 8 对抗训练

---

1. 偏差与方差

偏差：度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力

方差：度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响

噪声：表达了在当前任务上任何学习算法所能够达到的期望泛化误差的下界，即刻画了学习问题本身难度。

1、训练集的错误率较小，而验证集/测试集的错误率较大，说明模型存在较大方差，可能出现了过拟合

2、训练集和测试集的错误率都较大，且两者相近，说明模型存在较大偏差，可能出现了欠拟合

3、训练集和测试集的错误率都较小，且两者相近，说明方差和偏差都较小，这个模型效果比较好。

2. 产生原因

欠拟合原因：训练样本数量少；模型复杂度过低；参数还未收敛就停止循环。

解决办法：增加样本数量；增加模型参数，提高模型复杂度；增加循环次数；查看是否是学习率过高导致模型无法收敛。

过拟合原因：数据噪声太大；特征太多；模型太复杂。

解决办法：清洗数据；减少模型参数，降低模型复杂度；增加惩罚因子（正则化），保留所有的特征，但是减少参数的大小（magnitude）。

3.解决欠拟合(高偏差)的方法

3.1 模型复杂化

对同一个算法复杂化。例如回归模型添加更多的高次项，增加决策树的深度，增加神经网络的隐藏层数和隐藏单元数等

弃用原来的算法，使用一个更加复杂的算法或模型。例如用神经网络来替代线性回归，用随机森林来代替决策树等。

3.2 增加更多的特征

使输入数据具有更强的表达能力，特征挖掘十分重要，尤其是具有强表达能力的特征，往往可以抵过大量的弱表达能力的特征。

3.3 调整参数和超参数

超参数包括：神经网络中：学习率、学习衰减率、隐藏层数、隐藏层的单元数、Adam优化算法中的β1和β2参数、batch_size数值等。

其他算法中：随机森林的树数量，k-means中的cluster数，正则化参数λ等。

3.4 增加训练数据(效果不明显）

欠拟合本来就是模型的学习能力不足，增加再多的数据给它训练它也没能力学习好

3.5 降低正则化约束

正则化约束是为了防止模型过拟合，如果模型压根不存在过拟合而是欠拟合了，那么就考虑是否降低正则化参数λ或者直接去除正则化项

4. 解决过拟合(高方差)的方法

 4.1 增加训练数据数

发生过拟合最常见的现象就是数据量太少而模型太复杂

过拟合是由于模型学习到了数据的一些噪声特征导致，增加训练数据的量能够减少噪声的影响，让模型更多地学习数据的一般特征。

4.2 使用正则化约束

在代价函数后面添加正则化项，可以避免训练出来的参数过大从而使模型过拟合。使用正则化缓解过拟合的手段广泛应用，不论是在线性回归还是在神经网络的梯度下降计算过程中，都应用到了正则化的方法。

4.3 批归一化 BN

 批量归一化（Batch Normalization，BN）方法，即在模型每次随机梯度下降训练时，通过mini-batch来对每一层卷积的输出做规范化操作，使得结果（各个维度）的均值为0，方差为1

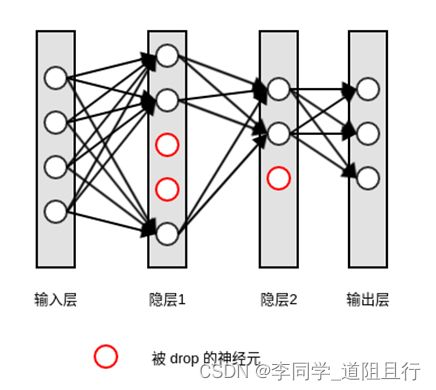
4.4 使用Dropout

这一方法只适用于神经网络中，即按一定的比例去除隐藏层的神经单元，使神经网络的结构简单化

4.5 提前结束训练

即earlystopping，在模型迭代训练时候记录训练精度(或损失)和验证精度(或损失)，倘若模型训练的效果不再提高，比如训练误差一直在降低但是验证误差却不再降低甚至上升，这时候便可以结束模型训练了。

4.6 减少特征数

欠拟合需要增加特征数，那么过拟合自然就要减少特征数。去除那些非共性特征，可以提高模型的泛化能力。

4.7 调整参数和超参数

4.8 降低模型的复杂度

欠拟合要增加模型的复杂度，那么过拟合正好反过来

5.正则化 

 5.1 L1、L2正则化(Regularization)

在成本函数中加入一个正则化项(惩罚项)，惩罚模型的复杂度，防止网络过拟合。简单的模型比复杂的泛化能力好。

网络越大，训练数据学习的速度就越快（使训练损失很快降低），但是也更容易过拟合（导致训练和验证损失之间的巨大差异）。

逻辑回归的参数W数量根据特征的数量而定，那么正则化如下

L1 正则化是权重向量 w 中各个元素的绝对值之和，L1 正则化增加了所有权重 w 参数的绝对值之和逼迫更多 w 为零，也就是变稀疏，稀疏规则的一个关键原因在于它能实现特征的自动选择。L1 正则化实现特征自动选择，它会学习地去掉这些无用的特征，也就是把这些特征对应的权重置为 0。

L2 正则化是权重向量w中各个元素的平方和然后再求平方根。逼迫所有w尽可能趋向零但不为零（L2 的导数趋于零）

L1和L2区别：

L1是模型各个参数的绝对值之和；L2是模型各个参数的平方和的开方值。

L1会趋向于产生少量的特征，而其他的特征都是0；L2会选择更多的特征，这些特征都会接近于0。

 5.2 正则化为什么能够防止过拟合

正则化因子设置的足够大的情况下，为了使成本函数最小化，权重矩阵 W 就会被设置为接近于 0 的值，直观上相当于消除了很多神经元的影响，那么大的神经网络就会变成一个较小的网络。

当λ增大时，偏差增大，方差减小

 6 Droupout丢弃法

Droupout论文地址：http://jmlr.org/papers/volume15/srivastava14a.old/srivastava14a.pdf

Droupout：随机的对神经网络每一层进行丢弃部分神经元操作。

对于网络的每一层会进行设置保留概率，即keep_prob。假设keep_prob为0.8，那么也就是在每一层所有神经元有20% 的概率直接失效，可以理解为0.

加入了 dropout 后，输入的特征都存在被随机清除的可能，所以该神经元不会再特别依赖于任何一个输入特征，也就是不会给任何一个输入特征设置太大的权重。 

7 数据增强

数据增强：指通过剪切、旋转/反射/翻转变换、缩放变换、平移变换、尺度变换、对比度变换、噪声扰动、颜色变换等一种或多种组合数据增强变换的方式来增加数据集的大小。

7.1 线性变换

常见的图片数据集增强方法：

将训练图像沿着每个方向平移几个像素产生新的图像。

对训练图像进行旋转、翻转或者缩放。

对训练图像进行随机裁剪（也可以被认为是预处理步骤）

对训练图像进行颜色抖动：调整饱和度、调整亮度、调整对比度、调整锐度。

对比度：图像画面的明暗反差程度。对比度越高，则图片亮的地方更亮，暗的地方越暗。

亮度：图像的明暗程度。亮度越高，则图像整体越亮。

饱和度：图像颜色种类的多少。饱和度越高，则图像的颜色种类越多，图像越鲜艳。 

锐度：图像的边缘轮廓的锐利程度。锐度越高，则图像的边缘越清晰。

7.2 标签平滑

假设训练数据集中有一些样本的标签是被错误标注的，那么最小化这些样本上的损失函数会导致过拟合．一种改善的正则化方法是标签平滑（Label Smoothing），即在输出标签中添加噪声来避免模型过拟合

 8 对抗训练

对输入点 ，我们搜寻它的附近的一个人眼看起来没有区别、网络预测结果差异很大的样本；输入点来自于训练集，称作原始样本；而是人工构造的，称作对抗样本。

将生成的对抗样本加入到训练集中去，做一个数据增强，让模型在训练的时候就先学习一遍对抗样本。

对抗训练通过鼓励网络在训练数据附近的局部区域保持稳定来限制函数对输入扰动的高度敏感性。